
�}Ŀ�б�(�����𰸺ͽ���)
20. �ⷨһ��
�ⷨһ��
(I)���}�⣬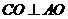 ��
��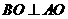 ��
��
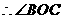 �Ƕ����
�Ƕ���� ��ƽ��ǣ�
��ƽ��ǣ�
�� �����
����� ��ֱ����ǣ�
��ֱ����ǣ�
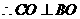 ����
����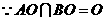 ��
��
 ƽ��
ƽ�� ��
��
��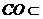 ƽ��
ƽ�� ��
��
 ƽ��
ƽ��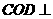 ƽ��
ƽ�� ��--------------------------------------------------------4��
��--------------------------------------------------------4��
(II)��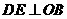 �������
�������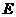 ���B�Y(ji��)
���B�Y(ji��) (��D)���t
(��D)���t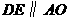 ��
��
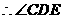 �Ǯ���ֱ��
�Ǯ���ֱ�� �c
�c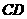 ���ɵĽǣ�----------------------------------5��
���ɵĽǣ�----------------------------------5��
�� ��
��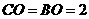 ��
��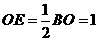 ��
��
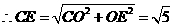 ��
��
��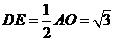 ��
��
 ��
�� ��
��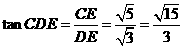 ��---------------------------------------7��
��---------------------------------------7��
 ����ֱ��
����ֱ�� �c
�c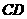 ���ɽǵĴ�С��
���ɽǵĴ�С��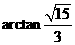 ��---------------------------------------8��
��---------------------------------------8��
(III)��(I)֪�� ƽ��
ƽ�� ��
��
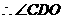 ��
��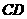 �cƽ��
�cƽ�� ���ɵĽǣ���
���ɵĽǣ���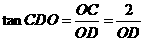 ��
��
��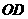 ���r��
���r�� ���------------------------------------10��
���------------------------------------10��
�@�r��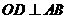 �������
�������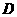 ��
��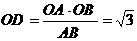 ��
��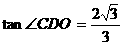 ��
��
 �cƽ��
�cƽ�� ���ɽǵ����ֵ��
���ɽǵ����ֵ��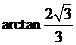 ��-----------------------------12��
��-----------------------------12��
19.�⣺(1)���}�⣬�ã�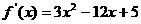 ��
�� ����
����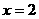
���� ���Թ��c������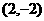 ����������������������������
����������������
3��
����������������������������
����������������
3��
(2����һ����(1)֪�����c��������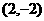 ,��
,��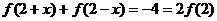 ������
������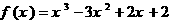 �P(gu��n)���c
�P(gu��n)���c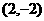 ���Q��
���Q��
���������O(sh��)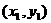 �c
�c �P(gu��n)��
�P(gu��n)��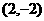 �����Q������
�����Q������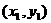 ��
��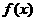 �����Ծ���
�����Ծ���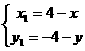 ����
���� ����
����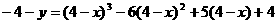
�����ģ�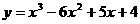
�����c Ҳ��
Ҳ��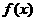 �ϣ���
�ϣ���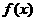 �P(gu��n)���c
�P(gu��n)���c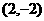 ���Q��������
�������������� 7��
���Q��������
�������������� 7��
һ��ģ����κ���(sh��)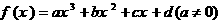 �ġ����c����
�ġ����c����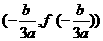 �������Ǻ���(sh��)
�������Ǻ���(sh��)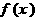 �Č��Q����(���ߣ��κ�һ�����κ���(sh��)���й��c���κ�һ�����κ���(sh��)���Ќ��Q���ģ��κ�һ�����κ���(sh��)ƽ�ƺ�������溯��(sh��)��������������)�����Խo�֡�����������������������������������������������������
����������������
10��
�Č��Q����(���ߣ��κ�һ�����κ���(sh��)���й��c���κ�һ�����κ���(sh��)���Ќ��Q���ģ��κ�һ�����κ���(sh��)ƽ�ƺ�������溯��(sh��)��������������)�����Խo�֡�����������������������������������������������������
����������������
10��
(3)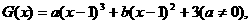 ��?q��)���һ�����w����(sh��)����
��?q��)���һ�����w����(sh��)����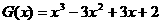 ����
����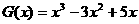 ����������
����������������
12��
����������
����������������
12��
���|(zh��)���κ�һ�����κ���(sh��)���й��c���κ�һ�����κ���(sh��)���Ќ��Q���ģ����κ�һ�����κ���(sh��)�ġ����c���������Č��Q���ģ�����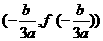
18.�⣺�ȕ������֕��������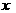 �ˣ��t�Ċ���й���(7��
�ˣ��t�Ċ���й���(7��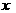 )�ˣ�
)�ˣ�
��ôֻ��һ헵��˔�(sh��)��(7��2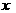 )��
)��
(1)�� ��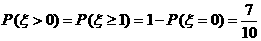
����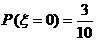 ��
��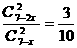 ���
���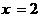
���Ċ�꠹���5�ˣ�---------------------------------------------------------------------------------4��
(2) ����ȡ��ֵ�飺0��1��2-------------------------------------------------------------6��
����ȡ��ֵ�飺0��1��2-------------------------------------------------------------6��
�t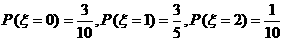 -----------------------------------------8��
-----------------------------------------8��
 �ķֲ��О�
�ķֲ��О�
 |
0 |
1 |
2 |
|
P |
3��10 |
3��5 |
1��10 |
---------------------------------------------------10��
�t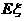 ��
�� -----------------------------------------------------------------------12��
-----------------------------------------------------------------------12��
17.���ɗl����
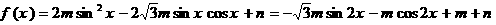
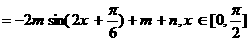 --------------------------------4��
--------------------------------4��
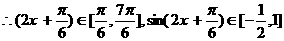 --------------------------6��
--------------------------6��
��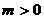 �r��
�r��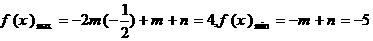
��ã�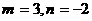 ���Ķ�
���Ķ�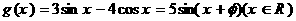
�������ֵ��5����Сֵ��-5��---------------------------------------8��
��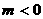 �r��
���
�r��
���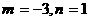 ��
��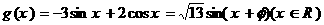
�������ֵ��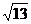 ����Сֵ��
����Сֵ��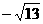 ��--------------------------------10�֡�������������������������������������������
������������������������
��--------------------------------10�֡�������������������������������������������
������������������������
13. 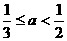 ����14.
����14. 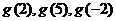 ����15�� 1���� 16.
����15�� 1���� 16. 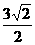 ��
��
22. (���} 12��) �O(sh��)��(sh��)�� ��ǰ
��ǰ 헺͞�
헺͞� ����һ��
����һ��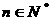 ���c
���c ���ں���(sh��)
���ں���(sh��) �ĈD���ϡ�
�ĈD���ϡ�
(��)��(sh��)�� ��ͨ헹�ʽ��
��ͨ헹�ʽ��
(��)����(sh��)�� ���ΰ�1헡�2헡�3헡�4�ѭ�h(hu��n)�ط֞�
���ΰ�1헡�2헡�3헡�4�ѭ�h(hu��n)�ط֞�
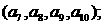
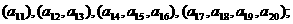
 �քeӋ�������̖��(n��i)����(sh��)֮�ͣ��O(sh��)���@Щ�Ͱ�ԭ����̖��ǰ�����(g��u)�ɵĔ�(sh��)��
�քeӋ�������̖��(n��i)����(sh��)֮�ͣ��O(sh��)���@Щ�Ͱ�ԭ����̖��ǰ�����(g��u)�ɵĔ�(sh��)�� ����
����
(��)�O(sh��) �锵(sh��)��
�锵(sh��)�� ��ǰ
��ǰ 헷e���Ƿ���ڌ���(sh��)
헷e���Ƿ���ڌ���(sh��) ��ʹ�ò���ʽ
��ʹ�ò���ʽ ��һ��
��һ��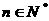 �������������ڣ����
�������������ڣ���� ��ȡֵ�������������ڣ�Ո�f�����ɡ����� ������
��ȡֵ�������������ڣ�Ո�f�����ɡ����� ������
2008-2009�W��ȵڶ��W�����п�ԇ�����꼉��(sh��)�Wԇ���� (����) ��
һ���x���}��BACCB�� AACAC�� DA
21.(���}�M�� 12��)��ABC��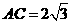 ��B�ǙE�A
��B�ǙE�A ��x�S�Ϸ�����c��
��x�S�Ϸ�����c�� ���p����
���p���� λ��x�S�·��Ĝʾ�����AC��ֱ��
λ��x�S�·��Ĝʾ�����AC��ֱ�� ���\�ӕr��
���\�ӕr��
(1)���ABC��ӈA�ĈA��P��܉�EE�ķ��̣�
(2)�^���c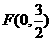 �����ഹֱ��ֱ��
�����ഹֱ��ֱ��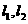 ���քe��܉�EE��M��N��R��Q������߅��MRNQ��e����Сֵ��
���քe��܉�EE��M��N��R��Q������߅��MRNQ��e����Сֵ��
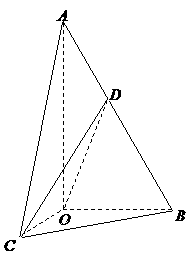
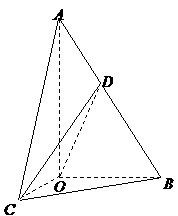
20. (���}�M��12��) ��D����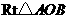 ��
�У�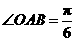 ��б߅
��б߅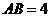 ��
��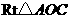 ����ͨ�^
����ͨ�^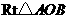 ��ֱ��
��ֱ�� ���S���D(zhu��n)�õ����Ҷ����
���S���D(zhu��n)�õ����Ҷ���� ��ֱ����ǣ����c
��ֱ����ǣ����c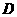 ��б߅
��б߅ �ϣ�
�ϣ�
(I)���C��ƽ��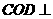 ƽ��
ƽ�� ��
��
(II)��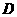 ��
�� �����c�r������ֱ��
�����c�r������ֱ�� �c
�c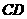 ���ɽǵĴ�С��
���ɽǵĴ�С��
(III)��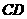 �cƽ��
�cƽ�� ���ɽǵ����ֵ��
���ɽǵ����ֵ��
19.(���}�M��12��)���������(sh��)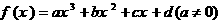
���x���O(sh��)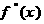 �Ǻ���(sh��)
�Ǻ���(sh��)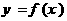 �Č���(sh��)
����(sh��) ����(sh��)��������
�Č���(sh��)��������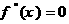 �Ќ���(sh��)��
�Ќ���(sh��)�� ���t�Q�c
���t�Q�c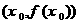 �麯��(sh��)
�麯��(sh��)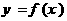 �ġ����c����
�ġ����c����
��֪����(sh��)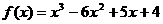 ��Ո�ش����І��}��(1)��(sh��)
��Ո�ش����І��}��(1)��(sh��)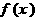 �ġ����c��
�ġ����c��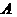 ������
������
(2)������
 �z��(sh��)
�z��(sh��)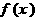 �ĈD���Ƿ��P(gu��n)�ڡ����c��
�ĈD���Ƿ��P(gu��n)�ڡ����c��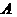 ���Q��������������κ���(sh��)����һ�����P(gu��n)�����c���ĽY(ji��)Փ��(3)����һ�����κ���(sh��)
���Q��������������κ���(sh��)����һ�����P(gu��n)�����c���ĽY(ji��)Փ��(3)����һ�����κ���(sh��)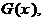 ʹ�����ġ����c����
ʹ�����ġ����c����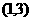 (��Ҫ�^��)
(��Ҫ�^��)
18. (���}�M��12��) �WУ�Ċ�꠵�ÿλ꠆T���衢�������ٕ�һ헣���֪���������2�ˣ����������5�ˣ��F(xi��n)�����x2�ˣ��O(sh��) ���x�������мȕ������֕�������˔�(sh��)����
���x�������мȕ������֕�������˔�(sh��)����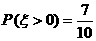
(1)������ ���Ċ�꠵��˔�(sh��)��
(2)������ ���� �ĸ��ʷֲ��в�Ӌ��
�ĸ��ʷֲ��в�Ӌ��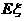 ��
��
���H�WУ��(y��u)�x - �������б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��ƽ�_ | �W(w��ng)���к���Ϣ�e�^(q��) | ����p�_�e�^(q��) | ��vʷ̓�o���x�к���Ϣ�e�^(q��) | �����֙�(qu��n)�e�^(q��)
�`���Ͳ�����Ϣ�e���Ԓ��027-86699610 �e���]�䣺58377363@163.com