
題目列表(包括答案和解析)
(二)填空題
16.直線xsinα+ycosα=m(常量α∈(0,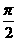 )) 被圓x2+y2=2所截的弦長為
)) 被圓x2+y2=2所截的弦長為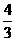
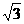 ,則m= .
,則m= .
17.拋物線y2=4x的弦AB垂直于x軸,若AB的長為4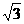 ,則焦點到AB的距離為 .
,則焦點到AB的距離為 .
18.如果方程x2cos2θ+y2sinθ=1,表示橢圓,那么θ 角的取值范圍是 .
19.設F1、F2是雙曲線 =1(a >0,b>0)的兩個焦點,P為雙曲線上的一點,P與F1、F2的連線互相垂直,且∠PF1F 2=15°,則雙曲線的離心率為
.
=1(a >0,b>0)的兩個焦點,P為雙曲線上的一點,P與F1、F2的連線互相垂直,且∠PF1F 2=15°,則雙曲線的離心率為
.
(一)選擇題
1.“點M的坐標是方程f(x,y)=0的解”是“點M在方程f(x,y)=0曲線上”的( )
A.充分不必要條件 B.必要不充分條件
C.充要條件 D.既非充分又非必要條件
2.已知圓C的方程為f(x,y)=0,點A(x0,y0)是圓C外的一點,那么方程f(x,y)-f(x0,y0)=0表示的曲線( )
A.可能不是圓
B.是與圓C重合的圓
C.是過A點與圓C相交的圓
D.是過A點且與圓C同心的圓
3.橢圓(1-m)x2-my2=1的長軸長是( )
A.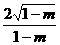 B.
B. 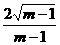
C. 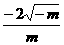 D.
D.
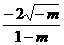
4.下列各對雙曲線中,既有相同離心率又有相同漸近線的是( )
A.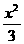 -y2=1和
-y2=1和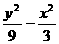 =1 B.
=1 B. 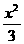 -y2=1和y2-
-y2=1和y2-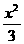 =1
=1
C.y2-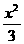 =1和x2-
=1和x2-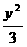 =1
D.
=1
D. 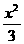 -y2=-1和
-y2=-1和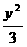 -
- =1
=1
5.拋物線y=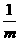 x2(m<0)的焦點坐標是( )
x2(m<0)的焦點坐標是( )
A.(0,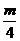 )
B.(0,-
)
B.(0,- 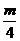 )
)
C.(0, 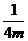 )
D.(0,-
)
D.(0,- 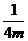 )
)
6.已知橢圓 =1 (a>b>0)的兩 個焦點把夾在兩條準線間的線段三等分,那么這個橢圓的離心率是( )
=1 (a>b>0)的兩 個焦點把夾在兩條準線間的線段三等分,那么這個橢圓的離心率是( )
A.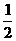 B.
B. 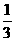 C.
C.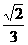 D.
D. 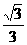
7.過拋物線y2=2px(p>0)的焦點作一條直線l交拋物線于A(x1,y1),B(x2,y2)兩點
,則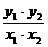 的值為( )
的值為( )
A.4 B.-4 C.p2 B.-p2
8.過雙曲線的一個焦點,有垂直于實軸的弦PQ,F′是另一個焦點,若∠PF′Q=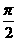 ,則雙曲線離心率是( )
,則雙曲線離心率是( )
A.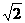 +2 B.
+2 B. 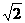 +1 C.
+1 C. 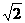 D.
D. 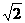 -1
-1
9.x2+2x+y2+4y-3=0上到直線x+y+1=0的距離為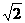 的點共有( )
的點共有( )
A.1個 B.2個 C.3個 D.4個
10.橢圓的兩準線方程分別為x=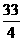 ,x=-
,x=- ,一個 焦點坐標為(6,2),則橢圓方程是( )
,一個 焦點坐標為(6,2),則橢圓方程是( )
A. =1 B.
=1 B. 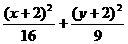 =1
=1
C. 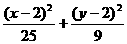 =1 D.
=1 D. 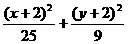 =1
=1
11.設雙曲線 =1的兩條漸近線含 實軸的夾角為θ,而離心率e∈[
=1的兩條漸近線含 實軸的夾角為θ,而離心率e∈[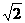 ,2],則θ的取值范圍是( )
,2],則θ的取值范圍是( )
A.[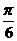 ,
,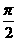 ] B.[
] B.[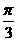 ,
,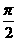 ] C.[
] C.[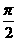 ,
,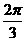 ] D.[
] D.[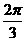 , π]
, π]
12.圓心在拋物線x2=2y上,且與y軸和該拋物線的準線都相切的一個圓的方程是( )
A.x2+y2-x-2y-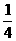 =0
B.x2+y2+x-2y+1=0
=0
B.x2+y2+x-2y+1=0
C.x2+y2+2x-y+1=0
D.x2+y2-2x-y+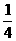 =0
=0
13.和x軸相切,且和圓x2+y2=1外切的動圓圓心的軌跡方程是( )
A.x2=2y+1 B.x2=-2y+1
C.x2=2y+1或x2=-2y+1 D.x2=2│y│+1
14.已知A={(x,y)|x2+y2=1},B={(x,y)|y2=2(x-a)};若A∩B=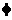 ,則實數a的取值 范圍是( )
,則實數a的取值 范圍是( )
A.a<-1 B.a>1 C.a<-2 D.a<-1或a>1
15.已知0<a<1<b,那么曲線a2x2-a2y2=logab是( )
A.焦點在x軸的雙曲線
B.焦點在y軸的橢圓
C.焦點在x軸的等軸雙曲線
D.焦點在y軸的等軸雙曲線
(八)綜合例題賞析
例9 設甲、乙、丙是三個命題,如果甲是乙的必要條件;丙是乙的充分條件但不是乙的必要條件,那么( )
A.丙是甲的充分條件,但不是必要條件
B.丙是甲的必要條件,但不是甲的充分條件
C.丙是甲的充要條件
D.丙不是甲的充分條件,也不是甲的必要條件
解
“甲是乙的必要條件”,即“甲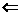 乙”,“丙是乙的充分不必要條件”,即“丙
乙”,“丙是乙的充分不必要條件”,即“丙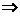 乙, 且丙
乙, 且丙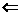 乙”。
乙”。
因
丙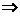 乙
乙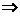 甲
甲
即丙是甲的充分不必要條件
故 應選A.
例10 已知直線x=a(a>0)和圓(x-1)2+y2=4相切 ,那么a的值是( )
A.5 B.4 C.3 D.2
解:r=2,圓心(1,0),a>0,∴a=3
應選C.
例11 設圓滿足:①截y軸所得的弦長為2;②被x軸分成 的兩段弧,其弧長的比為3∶1在滿足條件①、②的所有圓中,求圓心到直線l∶x-2y=0的距 離最小的圓的方程
解:設所求圓的圓心P(a,b)半徑r
由題設知,P到x,y軸的距離分別為|b|,|a|,且圓P截x軸的弦所對圓心角為90°,故其弦 長為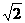 r,有r2=2b2
r,有r2=2b2
由“圓P截y軸所得弦長為2”有r2=a2+1
∴2b2-a2=1
P(a,b)到直線x-2y=0的距離為
d=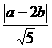 ,得
,得
5d2=|a-2b|2=a2+4b2-4ab≥a2+4b2-2(a2+b2)
2b2-a2=1
當且僅當a=b時上式等號成立,此時5d2=1從而d取得最小值
由此有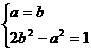 解得
解得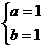 或
或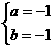
又由r2=2b2,得r2=2.
∴所求圓方程是(x-1)2+(y-1)2=2,或(x+1)2+(y+1)2=2
例12
已知圓滿足:①截y軸所得弦長為2;②被x軸分成兩段圓弧,其弧長的 比為3∶1;③圓心到直線l∶x-2y=0的距離為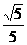 ,求該圓的方程
,求該圓的方程
解
設已知圓的圓心P(a,b),半徑為r,由題設已知圓P截x軸所得劣弧所對的圓心角是90°,從而圓P截x軸所得弦長為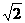 r,又點P到x,y軸的距離分別為|b|,|a|圓P 截y軸所得弦長為2。
r,又點P到x,y軸的距離分別為|b|,|a|圓P 截y軸所得弦長為2。
r2=a2+1 (1)
由已知有,點P到直線x-2y=0的距離為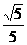 ,即
,即
d= (2)
(2)
由圓P截y軸的弦長為2,易知|b|=1 (3)
(2)、(3)聯立,可得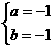 或
或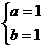 代入(1)又得r=
代入(1)又得r=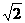
于是所求圓的方程為(x+1)2+(y+1)2或(x-1)2+(y-1)2=2
例13
設橢圓 =1 (a>b>0) 的右焦點為F1,右準線為l1.若過F1且垂直于x軸的弦的長等于點F1到l1的距離, 則橢圓的離心率是
.
=1 (a>b>0) 的右焦點為F1,右準線為l1.若過F1且垂直于x軸的弦的長等于點F1到l1的距離, 則橢圓的離心率是
.
解: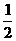
例14
設直線2x-y-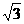 =0與y軸的交點為P,點P把圓(x+1)2+y2 =25的直徑分為兩段,則其長度之比是( )
=0與y軸的交點為P,點P把圓(x+1)2+y2 =25的直徑分為兩段,則其長度之比是( )
A.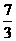 或
或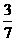 B.
B. 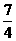 或
或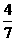 C.
C. 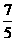 或
或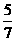 D.
D. 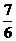 或
或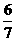
解:如下圖
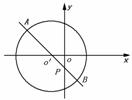
圓(x+1)2+y2=25的圓心坐標是(-1,0),半徑r=5。
直線l:2x-3-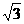 =0與y軸的交點P的坐標是(0,-
=0與y軸的交點P的坐標是(0,-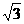 )。
)。
設點P在直徑AB上,所求即
|PA|∶|PB|。
由于|O′P|=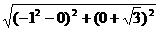 |=2
|=2
則 |PA|∶|PB|=(r+2)∶(r-2)=7∶3或
|PA|∶|PB|=(r-2)∶(r+2)=3∶7或
故 應選A。
例15
設雙曲線 =1(0<a<b)的半焦距為C,直線1過(a,0),(0,b)兩點,已知原點到直線1的距離為
=1(0<a<b)的半焦距為C,直線1過(a,0),(0,b)兩點,已知原點到直線1的距離為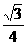 c,則雙曲線的離心率為( )
c,則雙曲線的離心率為( )
A.2. B.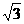 C.
C.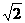 D.
D.
解:∵直線1過(a,0),(0,b),
∴1的方程為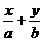 =1,
=1,
即bx+ay-ab=0
∵原點(0,0)到1的距離為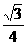 c,由點到直線的距離公式 ,得
c,由點到直線的距離公式 ,得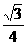 c=
c= 又0<a<b,雙曲線中c2=a2+b2,
又0<a<b,雙曲線中c2=a2+b2,
∴
整理得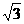 a2-4ab+
a2-4ab+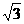 b2=0,b=
b2=0,b=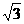 a.
a.
∴c2=a2+b2=4a2,c=2a,e=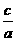 =2.
=2.
應選A.
例16
設F1和F2為雙曲線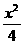 -y2 =1的兩個焦點,點P在雙曲線上且滿足∠F1PF2=90°.則△F1PF2的面積是( )
-y2 =1的兩個焦點,點P在雙曲線上且滿足∠F1PF2=90°.則△F1PF2的面積是( )
A.1 B.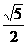 C.2
D.
C.2
D.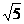
解:由已知可得,F1(-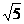 ,0),F2(
,0),F2(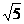 ,0)
,0)
∴|F1F2|=2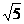 ,|F1F2|2=20
,|F1F2|2=20
由∠F1PF2=90°,
得20=|F1F2|2=|PF1|2+|PF2|2 ①
由雙曲線定義得︳PF1︳-︳PF2︳=2a=4,平方得
|PF1|2+|PF2|2-2|PF1|·︳PF1|=16 ②
①-②得2|PF1|·|PF2|=4
∴S△F1PF2=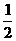 |PF1|·|PF2|
|PF1|·|PF2|
應選A.
例17
雙曲線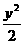 -x2=1的兩個焦點坐標是
.
-x2=1的兩個焦點坐標是
.
解:(0,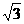 ),(0,-
),(0,-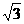 )
)
例18 如果雙曲線的實半軸長為2,焦距為6,那么該 雙曲線的離心率是( )
A.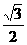 B.
B.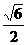 C.
C. D.2
D.2
解:由題設知a=2,c=3.
∴e= .
.
應選C.
例19 已知點(-2,3)與拋物線y2=2px(p>0)的焦點 的距離是5,則p= .
解:y2=2px的焦點坐標是(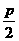 ,0),
,0),
∴5=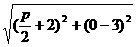
解出p=4.
例20 直線l過拋物線y2=a(x+1)(a>0)的焦點,并 且與x軸垂直,若l被拋物線截得的線段長為4,則a= .
解:設拋物線焦參數為p,則a=2p(p>0).
l是過焦點的直線且垂直于x軸即垂直于拋物線y2=a(x+1)的對稱軸.
∴l被拋物線截得的線段即正焦弦長.
∴4=2p=a,即a=4.
例21 如果三角形的頂點分別是O(0,0),A(0,15),B(-8 ,0),那么它的內切圓方程是 。
解:設內切圓心為O′,則O′到x、y軸等距,其距離即內切圓半徑r,又O′在第四象限木, 所以O′(r,-r)。
直線AB的方程是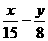 =1
=1 8x-15y-120=0
8x-15y-120=0
即±17r=23r-120,解得r=3(已舍負值)。
例22 焦點在(-1,0),頂點在(1,0)的拋物線方程是 ( )
A.y2=8(x+1) B.y2=-8(x+1)
C.y2=8(x-1) D.y2=-8(x-1)
解:設拋物線焦參數為p,則焦點和頂點的距離是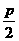 ,即
,即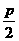 =
=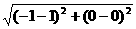 =2,得p=4.
=2,得p=4.
又拋物線頂點坐標為(1,0),焦點是(-1,0),
∴y2=-8(x-1)為所求.
應選D.
例23 圓x2+y2-2x=0和圓x2+y2-4x=0的位置關系是( )
A.相離 B.外切 C.相交 D.內切
解 C1∶(x-1)2+y2=1,O1(1,0),r1=1
C2∶x2+(y-2)2=4,O2(0,2),r2=2
因
|O1O2|=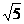 <r1+r2=3,且
<r1+r2=3,且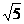 >|r1-r2|=1,
>|r1-r2|=1,
則 兩圓相交
應選C。
例24 設曲線C的方程是y=x3-x,將C沿x軸、y軸正 向分別平行移動t、s單位長度后得曲線C1.
(1)寫出曲線C1的方程;
(2)證明曲線C與C1關于點A(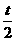 ,
,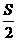 )對稱;
)對稱;
(3)如果曲線C與C1有且僅有一個公共點,證明S=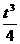 -t且t≠0.
-t且t≠0.
解:(1)曲線C1的方程為
y=(x-t)3-(x-t)+s
(2)在曲線C上任取點B1(x1,y1),設B2(x2,y2)是B1關于點A的對稱點,則有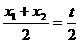 ,
,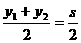 ,
,
∴x1=t-x2,y1=s-y2
代入曲線C的方程,得x2和y2滿足方程:
S-y2=(t-t2)3-(t-x2),
即y2=(x2-t)2-(x2-t)+s,
可知點B(x2-y2)在曲線C1上
反過來,同樣可以證明,在曲線C1上的點關于點A的對稱點在曲線C上,
∴曲線C與C1關于點A對稱.
(3)∵曲線C與C1有且僅有一個公共點,
∴方程組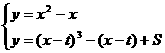 ,有且僅有一組解.
,有且僅有一組解.
消去y,整理得
3tx2-3t2x+(t3-t-S)=0,
這個關于x的一元二次方程有且僅有一個根
∴t≠0,并且其根的判別式
Δ=9t4-12t(t3-t-S)=0.
即
∴S=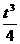 -t且t≠0
-t且t≠0
例25
已知橢圓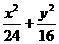 =1,直線L∶
=1,直線L∶ =1,P是L上
一點,射線OP交橢圓于R,又點Q在OP上且滿足│OQ│·│OP│=│OR│2,當點P在L上移動
時,求點Q的軌跡方程,并說明軌跡是什么曲線.
=1,P是L上
一點,射線OP交橢圓于R,又點Q在OP上且滿足│OQ│·│OP│=│OR│2,當點P在L上移動
時,求點Q的軌跡方程,并說明軌跡是什么曲線.
解:如圖.
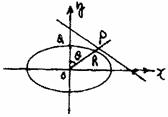
由題設知Q不在原點,設P、R、Q的坐標分別為(xP,yP)、(xR,yR)、(x,y)其中x ,y不同時為零.
當點P不在y軸上時,由于點R在橢圓上及點O、Q、R共線,得方程組;
 解得
解得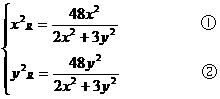
由于點P在直線l上及點O、Q、P共線,得方程組:
 ③,解得
③,解得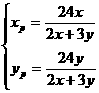 ④
④
當點P在y軸上時,經檢驗①-④也成立.
∵│OQ│·│OP│=│OR│2
∴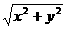 ·
·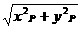
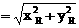 ,
,
將(1)-(4)代入上式,化簡整理得
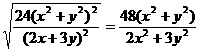 .
.
因x與xP同號或y與yP同號,以及③、④知2x+3y>0,
∴點Q的軌跡方程為 =1.其中(x,y不同時為零)
=1.其中(x,y不同時為零)
點Q的軌跡是以(1,1)為中心,長短半軸分別為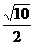 和
和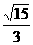 且長軸平行于x軸的橢圓.
且長軸平行于x軸的橢圓.
解法二:由題設知點Q不在原點.
設P、R、Q的坐標分別為(xP,yP),(xR,yR),(x,y)其中x,y不同時為零.
設OP寫x軸正方向的夾角為α,則有
xP=│OP│cosα,yP=│OP│sinα;
xR=│OR│cosα,yR=│OR│sinα;
x=│OQ│cosα,y=│OQ│sinα;
又│OP│·│OQ│=│OR│2,可得
 ①
① 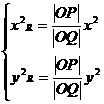 ②
②
∵點P在直線l上,點R在橢圓上,
∴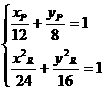 ,將(1)、(2)代
入,得
,將(1)、(2)代
入,得
 =1.(其中x,y不同時為零).
=1.(其中x,y不同時為零).
∴Q點的軌跡是以(1,1)為中心,長短半軸分別為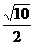 和
和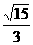 且長軸平行于x軸的橢圓(去掉坐標原點).
且長軸平行于x軸的橢圓(去掉坐標原點).
例26 已知直線L過坐標原點,拋物線C的頂點在原點、焦 點在x軸正半軸上,若點A(-1,0)和點B(0,8)關于L的對稱點都在C上,求直線L和拋物線的 方程.
解法一:如圖.
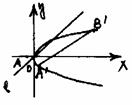
由題意可設拋物線C的方程為y2=2px (p>0),且x軸和y軸不是所求直線,又l過原點,所 以可設l的方程y=kx (k≠0)①
設A′、B′分別是A、B關于l的對稱點,則有,
A′A⊥l,直線AA′的方程為
y=-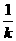 (x+1).②
(x+1).②
由①、②聯立得AA′與l的交點M的坐標為(-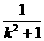 ,-
,-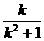 ).
).
由M為AA′的中點,得點A′的坐標為,
xA′=2(-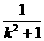 )+1=
)+1=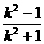 ,
,
yA′=2(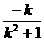 )+0=-
)+0=-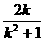 ③
③
同理可得點B的坐標為(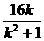 ,
,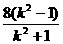 ).
).
∵A′、B′均在拋物線y2=2px (R>0)上,
∴(-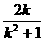 )2=2p·
)2=2p·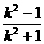 ,知k≠±1 ,p=
,知k≠±1 ,p=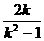 .
.
同理(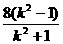 )2=2p·
)2=2p·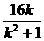 ,得p=
,得p=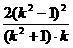 .
.
∴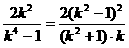 ,
,
整理得k2-k-1=0.
解得k1=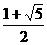 ,k2=
,k2=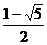 .
.
但當k=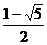 時,
時,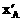 =-
=-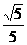 <0,與A′在拋物線y2=2px上矛盾,故舍去.
<0,與A′在拋物線y2=2px上矛盾,故舍去.
把k=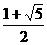 代入p=
代入p= .
.
∴直線方程為y=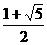 x,拋物線方程為y2=
x,拋物線方程為y2=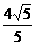 x.
x.
解法二:設點A、B關于直線l的對稱點A′(x1,y1)、B′(x2,y2),則有
│OA′│=│OA│=1,│OB′│=│OB│=8
設x軸正向到OB′的轉角為α,則有
x2=8cosα,y2=8sinα ①
∵A′,B′是A,B關于直線l的對稱點,
又∠BOA是直角,
∴∠B′OA′為直角,得
x1=cos(α-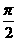 )=sin α,y1=sin(α-
)=sin α,y1=sin(α-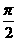 )=-cosα
②
)=-cosα
②
由題意知,x1>0,x2>0,故α為第一象限角.
∵A′,B′都在拋物線y2=2px上,
∴cos2α=2p·sinα,64sin2α=2p· cosα
∴8sin3α=cos3α,得2sinα=c osα
解得sinα=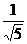 ,cosα=
,cosα=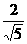 .
.
代入cos2α=2psinα,得p=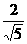 .
.
∴拋物線方程為y2=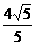 x.
x.
∵直線l平分∠BOB′,
∴l的斜率k=tg(α+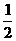 (
(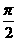 -α))=tg(
-α))=tg(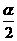 +
+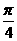 )
)
=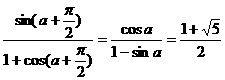 .
.
∴
直線l的方程為y=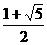 x.
x.
例27
在面積為1的△PMN中,tgM=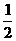 ,tgN=-2,建立適當的坐標系,求出M、N為焦點且過點P的橢圓方
程.
,tgN=-2,建立適當的坐標系,求出M、N為焦點且過點P的橢圓方
程.
解:如圖
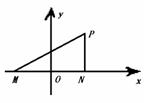
以MN所在直線為x軸,以線段MN的垂直平分線為y軸建立坐標系.
設以M、N為焦點且過P點的橢圓的方程為
 =1 (a>b>0)
=1 (a>b>0)
點M、N的坐標分別為(-c,0)、(c,0).
由tgM=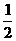 ,tg∠PNx=tg(π-∠MNP)=2,得
,tg∠PNx=tg(π-∠MNP)=2,得
直線PM和直線PN的方程分別為
y=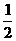 (x+c),y=2(x-c).
(x+c),y=2(x-c).
將兩方程聯立得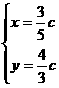 ,即P(
,即P( c,
c,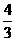 c).
c).
已知△MNP的面積為1,
∴1=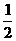 |MN|·yP=
|MN|·yP=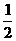 ·2c·
·2c·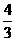 c=
c=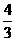 c2,
c2,
得c=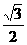 ,P(
,P(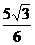 ,
,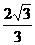 ).
).
∵|PM|=
=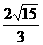 ,
,
|PN|=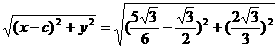
=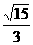 ,
,
∴2a=|PM|+|PN|= ,a=
,a=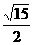 ,
,
b2=a2-c2=(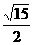 )2-(
)2-(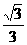 )2=3 .
)2=3 .
∴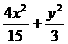 =1為所求橢圓方程.
=1為所求橢圓方程.
例28 自點A(-3,3)發出的光線L射到x軸上,被x軸反射,其反射光線所在直 線與圓x2+y2-4x-4y+7=0相切,求光線L所在的直線方程。
解 設反射光線為L′
由于 L和L′關于x軸對稱,L過點A(-3,3),點A關于x軸的對稱點A′(-3,-3),
于是 L′過A(-3,-3)。
設L′的斜率為k,則L′的方程為
y-(-3)=k[x-(-3)],即kx-y+3k-3=0,
已知圓方程即(x-2)2+(y-2)2=1,圓心O的坐標為(2,2),半徑r=1
因L′和已知圓相切,則O到L′的距離等于半徑r=1
即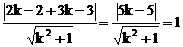
整理得12k2-25k+12=0
解得k=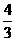 或k=
或k=
L′的方程為y+3=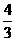 (x+3);或y+3=
(x+3);或y+3= (x+3)。
(x+3)。
即4x-3y+3=0或3x-4y-3=0
因L和L′關于x軸對稱
故L的方程為4x+3y+3=0或3x+4y-3=0。
例29
已知橢圓的中心在坐標原點O,焦點在坐標軸上,直線y=x+1
與該橢圓相交于P和Q,且OP⊥OQ,|PQ|=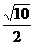 ,求橢圓的方程.
,求橢圓的方程.
解:設所求橢圓的方程為 =1.
=1.
依題意知,點P、Q的坐標滿足方程組:
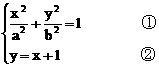
將②代入①,整理得
(a2+b2)x2+2a2x+a2(1-b2)=0, ③
設方程③的兩個根分別為x1、x2,則直線y=x+1和橢圓的交點為,
P(x1,x1+1),Q(x2,x2+1)
由題設OP⊥OQ,|OP|=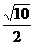 ,可得
,可得

整理得
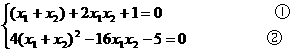
解這個方程組,得
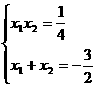 或
或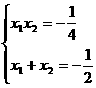
根據根與系數的關系,由(3)式得
(Ⅰ)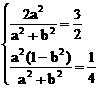 或 (Ⅱ)
或 (Ⅱ)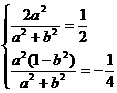
解方程組(Ⅰ)、(Ⅱ)得
 或
或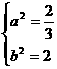
故所求橢圓方程為
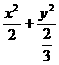 =1,或
=1,或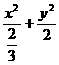 =1.
=1.
例30 如圖所示,給出定點A(a,0)(a>0)和直線l∶x=-1,B是直線l上的動 點,∠BOA的角平分線交AB于C,求點C的軌跡方程,并討論方程表示曲線類型與a值的關系。
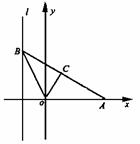
本小題主要考查曲線與方程,直線和圓錐曲線等基礎知識以及求動點軌跡的基本技能和綜合 運用數學知識解決問題的能力。
解法一 依題意,記B(-1,b)(b∈R),則直線OA和OB的方程分別為y=0和y=-bx。
設點C(x,y),則有0≤x<a,則OC平分∠AOB,知點C到OA、OB距離相等,根據點到直線的距 離公式得
|y|=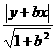 ①
①
依題設,點C在直線AB上,故有
y=-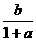 (x-a)
(x-a)
由x-a≠0得b=-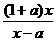 ②
②
將②式代入①式得
y2[1+ ]=[y-
]=[y-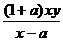 ]2
]2
整理得 y2[(1-a)x2-2ax+(1+a)y2]=0
若y≠0,則(1-a)x2-2ax+(1+a)y2=0(0<x<a=;
若y=0,則b=0,∠AOB=π,點C的坐標為(0,0),滿足上式,
綜上得點C的軌跡方程為
(1-a)x2-2ax+(1+a)y2=0(0≤x<a)。
(Ⅰ)當a=1時,軌跡方程化為y=x(0≤x<1); ③
此時,方程③表示拋物線孤段;
(Ⅱ)當a≠1時,軌跡方程化為
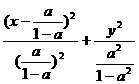 =1(0≤x<a)。
④
=1(0≤x<a)。
④
所以,當0<a<1時,方程④表示橢圓弧段。
當a>1時,方程④表示雙曲線一支的弧段。
解法二 如圖所示,設D是I與x軸的交點,過點C作CE⊥x軸,E是垂足。
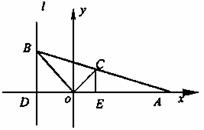
(Ⅰ)當|BD|≠0時,設點C(x,y),則0<x<a,y≠0。
由CE∥BD得
|BD|=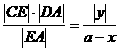 (1+a)
(1+a)
因 ∠COA=∠COB=∠COD-∠BOD
則 2∠COA=π-∠BOD,
tg(2∠COA)=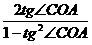 ,tg(π-∠BOD)=-tg∠BOD
,tg(π-∠BOD)=-tg∠BOD
又因 tg∠COA=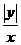 ,tg∠BOD=
(1+a)。
,tg∠BOD=
(1+a)。
故
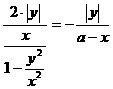 (1+a)。
(1+a)。
整理得 (1-a)x2-2ax+(1+a)y2=0 (0≤x<a)。
(Ⅱ)當|BD|=0時,∠BOA=π,則點C的坐標為(0,0),滿足上式。
綜合(Ⅰ),(Ⅱ),得點C的軌跡方程為
(1-a)x2-2ax+(1+a)y2=0(0≤x<a=。
例31 已知點P在直線x=2上移動,直線l通過原點且OP垂直 ,過點A(1,0)和點P的直線m和直線l交于點Q,求點Q的軌跡方程,并指出該軌跡的名稱和它 的焦點坐標.
解:設點P的坐標為(2,y1),則直線OP的斜率
kOP=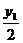 .
.
∵l⊥直線OP.
∴直線l的斜率k1滿足kOP·k1=-1,即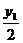 ·k1=-1,得k 1=-
·k1=-1,得k 1=-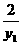 .
.
又直線l過原點,所以l的方程為y=-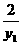 x.
x.
∵直線m過點A(1,0),P(2,y1).
∴m的方程為y1x-y-y1=0
由l的方程得y1=-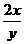 代入m的方程得-
代入m的方程得-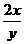 -y+
-y+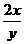 =0,即2x2+y2-2x=0.
=0,即2x2+y2-2x=0.
顯然點Q與點A(1,0)不重合,故x≠1.
又2x2+y2-2x=0可化為
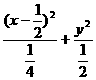 =1 (x≠1),
=1 (x≠1),
∴Q點的軌跡是挖去點(1,0)的橢圓,該橢圓的焦點坐標是(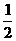 ,
,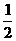 )和(
)和(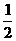 ,-
,-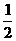 ).
).

[同步達綱練習]
(七)坐標軸的平移,利用坐標的平移化簡圓錐曲線方程
說明坐標軸的平移變換是化簡曲線方程的一種重要方法.掌握平移坐標軸的關鍵在于正確理解新舊坐標系之間的關系.同一個點在不同的坐標系中有不同的坐標,同一 條曲線在不同的坐標中有不同的方程.
例7 方程x2+4y2+6x-8y+1=0的對稱中心是( )
A.(-3,-1) B.(-3,1)
C.(3,-1) D.(3,1)
解: 將原方程配方后化為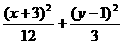 =1,∴ 對稱中心是(-3,1).故選B.
=1,∴ 對稱中心是(-3,1).故選B.
例8 求橢圓9x2+4y2-36x+8y+4=0的焦點坐標、長軸與短軸的長、離心率 及準線方程.
解: 將原方程配方后化成
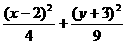 =1.
=1.
令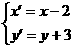 .得到新方程為
.得到新方程為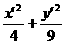 =1.
=1.
∴a=3,b=2,c= =
=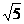 .
.
即長軸長2a=6,短軸長2b=4,離心率e=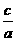 =
=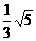 .在新坐標系中,焦點為(0,
.在新坐標系中,焦點為(0,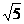 ),(0,-
),(0,-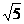 ),
),
準線為y′=±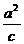 =±
=±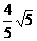
由平移公式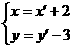 ,得在原坐標系中
,得在原坐標系中
焦點為:(2,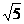 -3)、(2,-
-3)、(2,-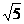 -3),
-3),
準線為:y=±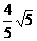 -3.
-3.
(六)拋物線及其標準方程,焦點、準線、拋物線的幾何性質:范圍、對稱 性、頂點、離心率,拋物線的畫法
說明 這部分內容要注意與初中講的拋物線y=ax2+bx+c(a≠0)的關系,以 及拋物線與雙曲線一支的區別,y=ax2+bx+c的對稱軸平行于y軸(或就是y軸),雙曲線有漸 近線,拋物線無漸近線.
例6 如圖,過拋物線y2=4x的頂點O作任意兩條互 相垂直的弦OM、ON,求(1)MN與x軸交點的坐標;(2)求MN中點的軌跡方程。
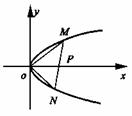
解
(1)設點M的坐標為(m,2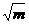 ),點N的坐標為(n,-2
),點N的坐標為(n,-2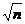 ),
),
由已知,OM2+ON2=MN2,則 m2+4m+n2+4n=(m-n)2+(2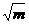 +2
+2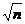 )2,mn=16。
)2,mn=16。
直線MN: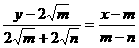
當y=0時,x= =4
=4
所以 MN與x軸交點的坐標為(4,0)。
(2)又因設弦MN的中點為P(x,y),

y2=m+n-2 =2x-8
=2x-8
故 弦MN的中點軌跡為y2=2x-8
(五)雙曲線及其標準方程,焦點、焦距,雙曲線的幾何性質:范圍、對稱 性、頂點、實軸、虛軸、漸近線、離心率、準線,雙曲線的畫法,等邊雙曲線
說明 根據已知條件會求雙曲線的標準方程,以及雙曲線的有關元素.這里與橢圓不同的是實軸、虛軸和漸近線.
例5
已知雙曲線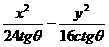 =1(
=1(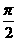 <θ<π)過點
<θ<π)過點
A(4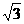 ,4).
,4).
(1)求實軸、虛軸的長;
(2)求離心率;
(3)求頂點坐標;
(4)求點A的焦半徑.
解: 因為雙曲線過點A(4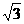 ,4),所以
,4),所以
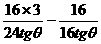 =1,tg2θ+tgθ-2=0 ,tgθ=-2,(tgθ=1舍去,因為
=1,tg2θ+tgθ-2=0 ,tgθ=-2,(tgθ=1舍去,因為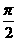 <θ<π)
<θ<π)
∴雙曲線方程為-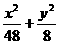 =1.
=1.
從而a=2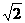 ,b=4
,b=4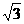 ,c=2
,c=2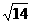 .
.
(1)實軸長2a=4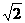 ,虛軸長2b=8
,虛軸長2b=8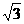 .
.
(2)離心率e=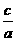 =
=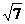 .
.
(3)頂點為(0,2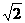 ),(0,-2
),(0,-2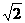 ).
).
(4)焦點F1(0,-2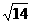 ),F2(0,2
),F2(0,2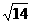 ).
).
|AF1|=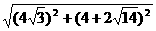
=2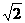 (
(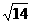 +1),
+1),
|AF2|=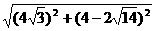
=2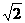 (
(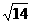 -1).
-1).
(四)橢圓及其標準方程,焦點、焦距,橢圓的幾何性質:范圍、對稱性、頂點、長袖、短軸、離心率、準線,橢圓的畫法
說明 天體的運行軌道基本都是橢圓,所以掌握橢圓的基本概念是很有必要的.考試說明中明確要求,要會求橢圓的標準方程和橢圓的有關元素.
例4
橢圓的中點在原點,焦點在x軸上,橢圓的離心率e=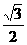 ,橢圓各點到直線x-y+
,橢圓各點到直線x-y+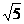 +
+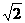 =0的最短距離為1,求此橢圓的方程 。
=0的最短距離為1,求此橢圓的方程 。
解
因為e=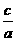 =
=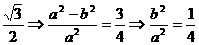 ,所以a=2b.
,所以a=2b.
設
M(2bcosθ,bsinθ)為橢圓上任一點,則M到直線x-y+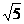 +
+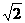 =0的 距離為
=0的 距離為
d=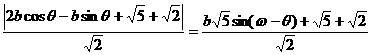 .
.
而d的最小值為1。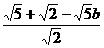 =1,則b=1,故所求橢圓方程為
=1,則b=1,故所求橢圓方程為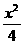 +y2=1.
+y2=1.
(三)圓的標準方程和一般方程
說明 求圓的方程主要是求出其圓心與半徑.還要掌握一般方程與標準方程 的互化,以及圓與其他曲線之間的關系,特別是圓與直線之間的關系.
例3 圓A:(x+1)2+(y+1)2=1,
圓B:(x-1)2+(y-1)2=4,則有兩圓的公切線有( )
A.1條 B.2條 C.3條 D.4條
解: 要判斷兩圓公切線的條數,只需要判斷出此兩圓的位置關系,而不必求出其切線方程 .∵A圓圓心是C1(-1,-1),B圓圓心是C2(1,1),∴|C1C2|=2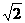 ,r1=1,r2=2.
,r1=1,r2=2.
r1+r2>|C1C2|即圓A與圓B相離,則此兩圓有4條公切線.故選D.
(二)充要條件
說明 充分條件、必要條件、充要條件是高考考查的重要內容.要掌握好這幾種條件,關鍵在于要對命題之間的關系很清楚.
例2 直線與平面平行的充要條件是這條直線與平面內的( )
A.一條直線不相交 B.兩條直線不相交
C.任意一條直線都不相交 D.無數條直線不相交
解:把“直線與平面平行”作為甲命題,在四個選項中選出一個是甲命題的充要條件的命題 。因為直線與平面平行的定義是直線與平面無交點,而A、B、D三個選項都 不能保證此條件,只有C能保證,故選C
(一)曲線和方程,由已知條件列出曲線的方程,曲線的交點
說明 在求曲線方程之前必須建立坐標系,然后根據條件列出等式進行化簡 .特別是在求出方程后要考慮化簡的過程是否是同解變形,是否滿足已知條件,只有這樣求 出的曲線方程才能準確無誤.另外,要求會判斷 曲線間有無交點,會求曲線的交點坐標.
例1 如果實數x、y滿足等式(x-2)2+y2=3,求y/x的最大值.
解: 此題有多種解法,但用待定參數,轉化為求曲線的交點問題可使解題過程更為簡捷.
設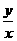 =k,則y=kx.要使k的值最大,只須直線y=kx在第一象限與圓相切
,而圓心(2,0)到直線y=kx的距離為
=k,則y=kx.要使k的值最大,只須直線y=kx在第一象限與圓相切
,而圓心(2,0)到直線y=kx的距離為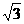 .
.
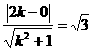 ,解得k=
,解得k=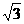 (-
(-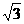 舍去).
舍去).
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com