
1.下列各組詞語(yǔ)中加點(diǎn)字的讀音全都正確的一項(xiàng)是 ( )
A.口訥(nè) 創(chuàng)可貼(chuàng) 鐘鼓饌玉(zuàn) 戛然而止(jiá)
B.弓繳(zhuó) 刀削面(xuē) 嘔心之作(ǒu) 蒞臨寒舍(wèi)
C.強(qiáng)顏(qiǎng) 汗涔涔(cén) 渾身解數(shù)(xiè) 禮節(jié)甚倨(jù)
D.俾倪(pínì) 相隨屬(zhǔ) 金蟬脫殼(qiòo) 暴殮天物(tiǎn)
(1)證明函數(shù)y= (
( +1)在(0,+∞)上是減函數(shù);
+1)在(0,+∞)上是減函數(shù);
(2)判斷函數(shù)y= (
( +1)在(-∞,0)上是增減性.
+1)在(-∞,0)上是增減性.
∴函數(shù) 在
在 上是增函數(shù)
上是增函數(shù)
證明:(1)設(shè) ,且
,且 ,則
,則

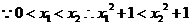
又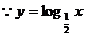 在
在 上是減函數(shù)
上是減函數(shù)
∴ 即
即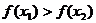
∴函數(shù)y= (
( +1)在(0,+∞)上是減函數(shù)?
+1)在(0,+∞)上是減函數(shù)?
(2)設(shè)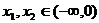 ,且
,且 ,則
,則

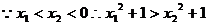
又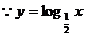 在
在 上是減函數(shù)
上是減函數(shù)
∴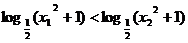 即
即
∴y= (
( +1)在(-∞,0)上是增函數(shù)
+1)在(-∞,0)上是增函數(shù)
3.已知y=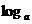 (2-
(2-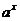 )在[0,1]上是x的減函數(shù),求a的取值范圍.
)在[0,1]上是x的減函數(shù),求a的取值范圍.
解:∵a>0且a≠1
當(dāng)a>1時(shí),函數(shù)t=2-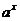 >0是減函數(shù)
>0是減函數(shù)
由y=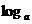 (2-
(2-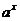 )在[0,1]上x的減函數(shù),知y=
)在[0,1]上x的減函數(shù),知y=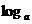 t是增函數(shù),
t是增函數(shù),
∴a>1
由x [0,1]時(shí),2-
[0,1]時(shí),2-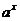
 2-a>0,得a<2,
2-a>0,得a<2,
∴1<a<2
當(dāng)0<a<1時(shí),函數(shù)t=2-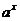 >0是增函數(shù)
>0是增函數(shù)
由y=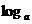 (2-
(2-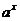 )在[0,1]上x的減函數(shù),知y=
)在[0,1]上x的減函數(shù),知y=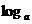 t是減函數(shù),
t是減函數(shù),
∴0<a<1
由x [0,1]時(shí),2-
[0,1]時(shí),2-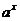
 2-1>0, ∴0<a<1
2-1>0, ∴0<a<1
綜上述,0<a<1或1<a<2
2.求函數(shù)y= (
( -4x)的單調(diào)遞增區(qū)間
-4x)的單調(diào)遞增區(qū)間
解:先求定義域:由 -4x>0得x(x-4)>0
-4x>0得x(x-4)>0
∴x<0或x>4
又函數(shù)y= t是增函數(shù)
t是增函數(shù)
故所求單調(diào)遞增區(qū)間為t= -4x在定義域內(nèi)的單調(diào)遞增區(qū)間
-4x在定義域內(nèi)的單調(diào)遞增區(qū)間
∵t= -4x的對(duì)稱軸為x=2
-4x的對(duì)稱軸為x=2
∴所求單調(diào)遞增區(qū)間為:(4,+∞)
1.求y= (
( -2x)的單調(diào)遞減區(qū)間
-2x)的單調(diào)遞減區(qū)間
解:先求定義域:由 -2x>0,得x(x-2)>0
-2x>0,得x(x-2)>0
∴x<0或x>2
∵函數(shù)y= t是減函數(shù)
t是減函數(shù)
故所求單調(diào)減區(qū)間即t= -2x在定義域內(nèi)的增區(qū)間
-2x在定義域內(nèi)的增區(qū)間
又t= -2x的對(duì)稱軸為x=1
-2x的對(duì)稱軸為x=1
∴所求單調(diào)遞減區(qū)間為(2,+∞)
例1 ⑴證明函數(shù) 在
在 上是增函數(shù)
上是增函數(shù)
⑵函數(shù) 在
在 上是減函數(shù)還是增函數(shù)?
上是減函數(shù)還是增函數(shù)?
⑴證明:設(shè) ,且
,且
則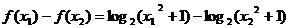
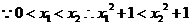

又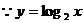 在
在 上是增函數(shù)
上是增函數(shù)
∴ 即
即
∴函數(shù) 在
在 上是增函數(shù)
上是增函數(shù)
⑵解:是減函數(shù),證明如下:
設(shè)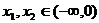 ,且
,且
則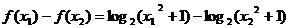
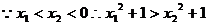
又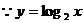 在
在 上是增函數(shù)
上是增函數(shù)
∴ 即
即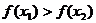
∴函數(shù) 在
在 上是減函數(shù)
上是減函數(shù)
小結(jié):復(fù)合函數(shù)的單調(diào)性
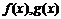 的單調(diào)相同,
的單調(diào)相同,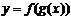 為增函數(shù),否則為減函數(shù)
為增函數(shù),否則為減函數(shù)
例2 求函數(shù) 的單調(diào)區(qū)間,并用單調(diào)定義給予證明
的單調(diào)區(qū)間,并用單調(diào)定義給予證明
解:定義域 
單調(diào)減區(qū)間是 設(shè)
設(shè)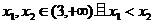 則
則
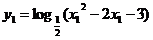

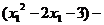
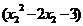 =
=
∵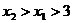 ∴
∴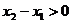

∴ >
>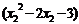 又底數(shù)
又底數(shù)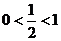
∴ 即
即 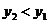
∴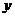 在
在 上是減函數(shù)
上是減函數(shù)
同理可證: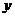 在
在 上是增函數(shù)
上是增函數(shù)
2.對(duì)數(shù)函數(shù)的性質(zhì):
|
|
a>1 |
0<a<1 |
|
圖 象 |
 |
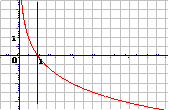 |
|
性 質(zhì) |
定義域:(0,+∞) |
|
|
值域:R |
||
過(guò)點(diǎn)(1,0),即當(dāng) 時(shí), 時(shí),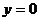 |
||
 時(shí) 時(shí) 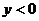   時(shí) 時(shí) 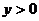  |
 時(shí) 時(shí) 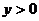   時(shí) 時(shí)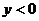  |
|
在(0,+∞)上是增函數(shù) |
在(0,+∞)上是減函數(shù) |
1.判斷及證明函數(shù)單調(diào)性的基本步驟:假設(shè)-作差-變形-判斷
22.(本小題滿分14分)
設(shè) 為實(shí)數(shù),函數(shù)
為實(shí)數(shù),函數(shù)
(Ⅰ)討論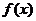 的奇偶性;
的奇偶性;
(Ⅱ)求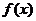 在
在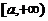 上的最小值.
上的最小值.
(Ⅲ)求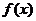 在
在 上的最小值.
上的最小值.
21.(本小題滿分12分)
某市居民自來(lái)水收費(fèi)標(biāo)準(zhǔn)如下:每戶每月用水不超過(guò)4噸時(shí)每噸為1.80元,當(dāng)用水超過(guò)4噸時(shí),超過(guò)部分每噸3.00元,某月甲、乙兩戶共交水費(fèi) 元,已知甲、乙兩用戶 該月用水量分別為
元,已知甲、乙兩用戶 該月用水量分別為 (噸)。
(噸)。
(1)求 關(guān)于
關(guān)于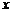 的函數(shù);
的函數(shù);
(2)若甲、乙兩戶該月共交水費(fèi)26.4元,分別求出甲、乙兩戶該月的用水量和水費(fèi)。(精確到0.1)
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com