
5. 線段AB=5cm,在以AB為直徑的圓上,到AB的距離為2.5cm的點有( )個。
A. 無數(shù)個 B. 1個 C. 2個 D. 4個
4. 用a、d分別表示圓的弦和直徑的長,則它們的關(guān)系是( )
A. 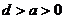 B.
B. 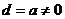
C. 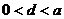 D.
D. 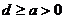
3. 下列說法中,不正確的是( )
A. 直徑相等的兩個圓是等圓
B. 同圓或等圓的半徑相等
C. 圓中的最大的弦是直徑
D. 一個圓只有一條直徑
2. 已知點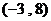 在反比例函數(shù)
在反比例函數(shù)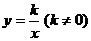 的圖象上,那么下列各點中在此函數(shù)圖象上的是( )
的圖象上,那么下列各點中在此函數(shù)圖象上的是( )
A. 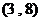 B.
B. 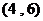 C.
C. 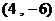 D.
D. 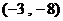
1. 在函數(shù)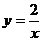 ,
,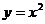 和
和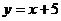 的圖象中,是中心對稱圖形,且對稱中心是原點的圖象共有( )
的圖象中,是中心對稱圖形,且對稱中心是原點的圖象共有( )
A. 0個 B. 1個 C. 2個 D. 3個
⒗(本小題滿分12分)在直角坐標(biāo)系中,已知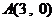 ,
,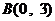 ,
,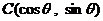 .
.
⑴若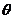 銳角,且
銳角,且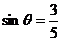 ,求
,求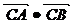 ;
;
⑵若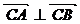 ,求
,求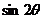 .
.
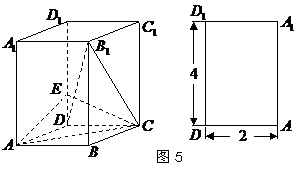 ⒘(本小題滿分13分)如圖5,已知正四棱柱
⒘(本小題滿分13分)如圖5,已知正四棱柱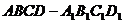 與它的側(cè)視圖(或稱左視圖),
與它的側(cè)視圖(或稱左視圖),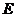 是
是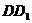 上一點,
上一點,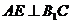 .
.
⑴求證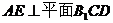 ;
;
⑵求三棱錐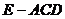 的體積.
的體積.
⒙(本小題滿分13分)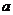 、
、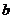 是常數(shù),關(guān)于
是常數(shù),關(guān)于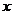 的一元二次方程
的一元二次方程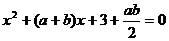 有實數(shù)解記為事件
有實數(shù)解記為事件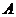 .
.
⑴若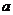 、
、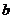 分別表示投擲兩枚均勻骰子出現(xiàn)的點數(shù),求
分別表示投擲兩枚均勻骰子出現(xiàn)的點數(shù),求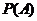 ;
;
⑵若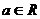 、
、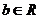 ,
,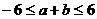 且
且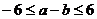 ,求
,求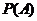 .
.
⒚(本小題滿分14分)已知圓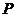 :
: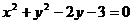 ,拋物線
,拋物線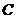 以圓心
以圓心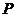 為焦點,以坐標(biāo)原點為頂點.
為焦點,以坐標(biāo)原點為頂點.
⑴求拋物線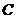 的方程;
的方程;
⑵設(shè)圓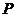 與拋物線
與拋物線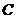 在第一象限的交點為
在第一象限的交點為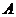 ,過
,過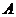 作拋物線
作拋物線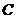 的切線與
的切線與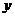 軸的交點為
軸的交點為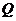 ,動點
,動點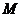 到
到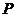 、
、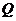 兩點距離之和等于
兩點距離之和等于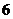 ,求
,求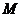 的軌跡方程.
的軌跡方程.
⒛(本小題滿分14分)已知函數(shù)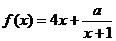 ,
,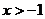 ,
,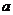 是常數(shù).
是常數(shù).
⑴若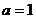 ,試證明
,試證明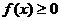 ;
;
⑵若對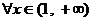 ,
,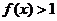 恒成立,求常數(shù)
恒成立,求常數(shù)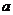 的取值范圍.
的取值范圍.
21.(本小題滿分14分)設(shè)數(shù)列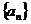 的前
的前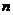 (
(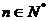 )項和為
)項和為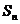 ,
,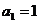 ,
,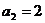 ,當(dāng)
,當(dāng)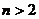 時,
時,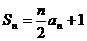 .
.
⑴求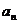 ;
;
⑵求數(shù)列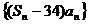 (
(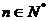 )最小的項.
)最小的項.
貴州省晴隆一中2009年高中畢業(yè)班強(qiáng)化訓(xùn)練
㈠必做題(11-13題)
 ⒒已知數(shù)列
⒒已知數(shù)列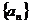 ,
,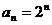 ,則
,則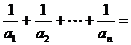 .
.
⒓雙曲線的一個焦點是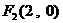 ,離心率
,離心率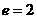 ,則
,則
雙曲線的標(biāo)準(zhǔn)方程是 .
⒔定義在實數(shù)集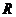 上的函數(shù)
上的函數(shù)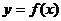 ,其對應(yīng)關(guān)系
,其對應(yīng)關(guān)系
由程序框圖(如圖3)給出,則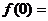 ,
,
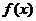 的解析式是 .
的解析式是 .
㈡選做題(14-15題,考生只能從中選做一題)
⒕(坐標(biāo)系與參數(shù)方程選做題)在平面直角坐標(biāo)系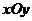 中,
中,
曲線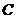 的參數(shù)方程為
的參數(shù)方程為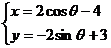 (參數(shù)
(參數(shù)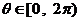 ).則曲線
).則曲線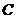 的普通方程
的普通方程
是
,曲線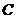 上的點到坐標(biāo)原點距離的最小值是
.
上的點到坐標(biāo)原點距離的最小值是
.
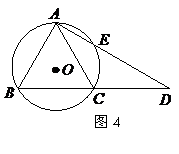 ⒖(幾何證明選講選做題)如圖4,
⒖(幾何證明選講選做題)如圖4,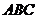 是圓
是圓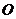 的內(nèi)接等邊
的內(nèi)接等邊
三角形, ,與
,與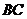 的延長線相交于
的延長線相交于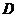 ,與圓
,與圓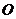
相交于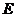 .若圓
.若圓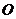 的半徑
的半徑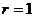 ,則
,則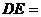 .
.
⒈設(shè)集合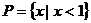 ,集合
,集合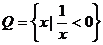 ,則
,則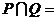
A.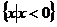 B.
B.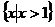 C.
C.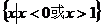 D.空集
D.空集
⒉若復(fù)數(shù)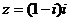 (
(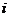 為虛數(shù)單位),則
為虛數(shù)單位),則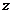 的共軛復(fù)數(shù)
的共軛復(fù)數(shù)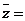
A.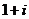 B.
B.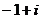 C.
C.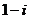 D.
D.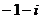
⒊已知命題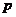 :
: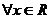 ,
,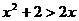 .則它的否定是
.則它的否定是
A.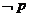 :
: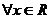 ,
,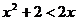 B.
B.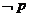 :
: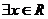 ,
,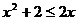
C.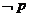 :
: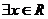 ,
, D.
D.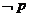 :
: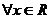 ,
,
⒋已知函數(shù)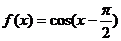 ,
,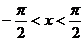 .則函數(shù)
.則函數(shù)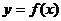 是
是
A.單調(diào)遞增的奇函數(shù) B.單調(diào)遞增的偶函數(shù)
C.單調(diào)遞減的奇函數(shù) D.單調(diào)遞減的偶函數(shù)
 ⒌已知向量
⒌已知向量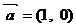 ,向量
,向量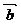 與
與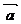 的夾角為
的夾角為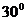 ,且
,且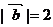 .則
.則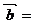
A.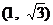 B.
B.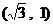 C.
C.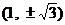 D.
D.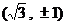
⒍已知某幾何體是一個圓柱和一個球的組合體,球的直徑和
圓柱底面直徑相等,它的正視圖(或稱主視圖)如圖1所示.
這個幾何體的表面積是
A.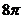 B.
B.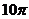 C.
C.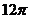 D.
D.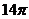
⒎若曲線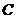 :
: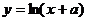 (
(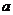 是常數(shù))經(jīng)過原點
是常數(shù))經(jīng)過原點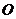 ,則曲線
,則曲線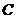 在
在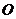 點的切線是
點的切線是
A.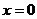 B.
B.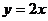 C.
C.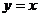 D.
D.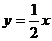
⒏隨機(jī)調(diào)查某校50個學(xué)生在“六一”兒童節(jié)的午餐費,結(jié)果如下表:
|
餐費(元) |
3 |
4 |
5 |
|
人數(shù) |
10 |
20 |
20 |
這50個學(xué)生“六一”節(jié)午餐費的平均值和方差分別是
A.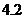 ,
,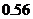 B.
B.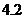 ,
,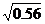 C.
C.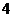 ,
,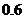 D.
D.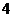 ,
,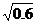
⒐在平面直角坐標(biāo)系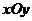 中,已知點
中,已知點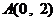 、
、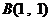 ,直線
,直線
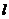 經(jīng)過點
經(jīng)過點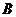 且與線段
且與線段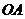 相交.則直線
相交.則直線
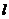 傾斜角
傾斜角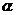 的取值范圍是
的取值范圍是
A.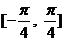 B.
B. 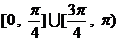 C.
C.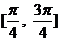 D.
D.
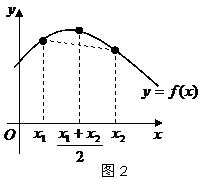 ⒑若對
⒑若對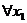 、
、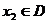 ,都有
,都有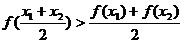 ,則稱區(qū)間
,則稱區(qū)間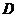 為函數(shù)
為函數(shù)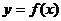 的一個凸區(qū)間(如圖2).在下列函數(shù)中,
的一個凸區(qū)間(如圖2).在下列函數(shù)中,
①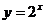 ;②
;②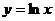 ;③
;③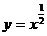 ;④
;④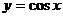
以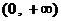 為一個凸區(qū)間的函數(shù)有:
為一個凸區(qū)間的函數(shù)有:
A.  個
B.
個
B. 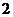 個
個
C. 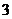 個 D.
個 D. 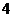 個
個
☆豎直上拋運動的實例分析
[例題]某人在高層樓房的陽臺外側(cè)以2 0 m/s的速度豎直向上拋出一個石塊,石塊運動到離拋出點15m處時,所經(jīng)歷的時間為多少?
(不計空氣阻力,取g =10m/s2)
分析:石塊運動到離拋出點15m處時,石塊的位置是在拋出點上方還是在拋出點下方?如果是在拋出點上方的話,是處于上升階段還是處于下降階段?
從題意來看,石塊拋出后能夠上升的最大高度為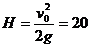 m>15m。
m>15m。
這樣石塊運動到離拋出點15 m處的位置必定有兩個,如圖所示,因而所經(jīng)歷的時間必為三個。
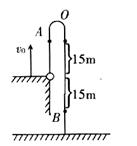
分段法:
石塊上升到最高點所用的時間為:
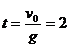 s
s
2 s前石塊第一次通過“離拋出點15 m處”;2 s時石塊到達(dá)最高點,速度變?yōu)榱悖S后石塊開始做自由落體運動,會第二次經(jīng)過“離拋出點15 m處”;當(dāng)石塊落到拋出點下方時,會第三次經(jīng)過“離拋出點15m處”。這樣此題應(yīng)有三解。
當(dāng)石塊在拋出點上方距拋出點15m處時取向上為正方向,則位移x = +15m,a= - g = - 10 m/s2 ,代入公式
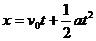
得: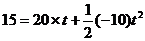
解得 t1=1 s;t2=3 s
t1=1 s對應(yīng)著石塊上升時到達(dá)“離拋出點15 m處”時所用的時間,而t2=3 s則對應(yīng)著從最高點往回落時第二次經(jīng)過“離拋出點15 m處”時所用的時間。
由于石塊上升的最大高度H=20m,所以,石塊落到拋出點下方“離拋出點15m處”時,自由下落的總高度為HOB=20m+15m=35m,下落此段距離所用的時間
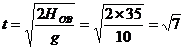 s
s
石塊從拋出到第三次經(jīng)過“離拋出點15m處”時所用的時間為:t3=2 s+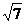 s=(2+
s=(2+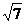 )s
)s
★課余作業(yè)
復(fù)習(xí)全章內(nèi)容,準(zhǔn)備章節(jié)測驗。
★教學(xué)體會
思維方法是解決問題的靈魂,是物理教學(xué)的根本;親自實踐參與知識的發(fā)現(xiàn)過程是培養(yǎng)學(xué)生能力的關(guān)鍵,離開了思維方法和實踐活動,物理教學(xué)就成了無源之水、無本之木。學(xué)生素質(zhì)的培養(yǎng)就成了鏡中花,水中月。
通過這節(jié)課的學(xué)習(xí),我們從伽利略對落體的研究上,學(xué)習(xí)他的觀察思考等科學(xué)方法,為我們下一步(以后)的探究打下基礎(chǔ),不能盲目,也不能怕困難,要用科學(xué)的方法指導(dǎo)我們。
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com