
6.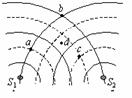 如圖所示,S1、S2是兩個(gè)相干波源,它們振動(dòng)同步且振幅相同。實(shí)線和虛線分別表示在某一時(shí)刻它們所發(fā)出的波的波峰和波谷。關(guān)于圖中所標(biāo)的a、b、c、d四點(diǎn),下列說法中正確的有( )
如圖所示,S1、S2是兩個(gè)相干波源,它們振動(dòng)同步且振幅相同。實(shí)線和虛線分別表示在某一時(shí)刻它們所發(fā)出的波的波峰和波谷。關(guān)于圖中所標(biāo)的a、b、c、d四點(diǎn),下列說法中正確的有( )
A.該時(shí)刻a質(zhì)點(diǎn)振動(dòng)最弱,b、c質(zhì)點(diǎn)振動(dòng)最強(qiáng),d質(zhì)點(diǎn)振
動(dòng)既不是最強(qiáng)也不是最弱
B.該時(shí)刻a質(zhì)點(diǎn)振動(dòng)最弱,b、c、d質(zhì)點(diǎn)振動(dòng)都最強(qiáng)
C.a質(zhì)點(diǎn)的振動(dòng)始終是最弱的, b、c、d質(zhì)點(diǎn)的振動(dòng)始終是最強(qiáng)的
D.再過T/4后的時(shí)刻a、b、c三個(gè)質(zhì)點(diǎn)都將處于各自的平衡位置,因此振動(dòng)最弱
5.關(guān)于電磁波和電磁場,下列敘述中正確的是( )
A.均勻變化的電場在它的周圍空間產(chǎn)生均勻變化的磁場
B.電磁波中每一處的電場強(qiáng)度和磁感應(yīng)強(qiáng)度總是互相垂直的,且與波的傳播方向垂直
C.電磁波和機(jī)械波一樣依賴于介質(zhì)傳播
D.只要空間某個(gè)區(qū)域有振蕩的電場或磁場,就能產(chǎn)生電磁波
4.A、B兩列波在某時(shí)刻的波形如圖所示,經(jīng)過t=TA時(shí)間(TA為波A的周期),兩波再次出現(xiàn)如圖波形,則兩波的波速之比vA:vB可能是( )
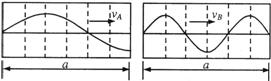 A.1:3 B.1:2
A.1:3 B.1:2
C.2:1 D.3:1
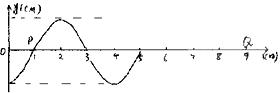
3.圖示表示一列簡諧波沿x軸正方向傳播在t=0時(shí)的波形圖,已知這列波在P點(diǎn)依次出現(xiàn)2個(gè)波峰的時(shí)間間隔為0.4s,則下列說法中正確的是:( )
A.這列波的波長是5m
B.這列波的波速是10m/s
C.質(zhì)點(diǎn)Q要再經(jīng)過0.7s才能第一次到達(dá)波峰處
D.質(zhì)點(diǎn)Q到達(dá)波峰時(shí),質(zhì)點(diǎn)P也恰好達(dá)到波峰處
2.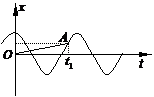 一個(gè)質(zhì)點(diǎn)做簡諧運(yùn)動(dòng),它的振動(dòng)圖象如圖,則(
)
一個(gè)質(zhì)點(diǎn)做簡諧運(yùn)動(dòng),它的振動(dòng)圖象如圖,則(
)
A.圖中的曲線部分是質(zhì)點(diǎn)的運(yùn)動(dòng)軌跡
B.有向線段OA是質(zhì)點(diǎn)在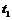 時(shí)間內(nèi)的位移
時(shí)間內(nèi)的位移
C.有向線段OA在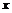 軸的投影是質(zhì)點(diǎn)在
軸的投影是質(zhì)點(diǎn)在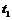 時(shí)間內(nèi)的位移
時(shí)間內(nèi)的位移
D.有向線段OA的斜率是質(zhì)點(diǎn)在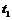 時(shí)刻的瞬時(shí)速率
時(shí)刻的瞬時(shí)速率
1.一個(gè)在水平方向做簡諧運(yùn)動(dòng)的彈簧振子的振動(dòng)周期是0.4s,當(dāng)振子從平衡位置開始向右運(yùn)動(dòng),在0.05s時(shí)刻,振子的運(yùn)動(dòng)情況是( )
A.正在向左做減速運(yùn)動(dòng) B.正在向右做加速運(yùn)動(dòng)
C.加速度正在減小 D.動(dòng)能正在減小
20.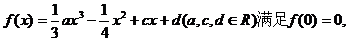 已知函數(shù)
已知函數(shù)
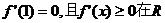 上恒成立
上恒成立
(1)求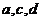 的值;
的值;
(2)若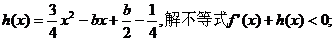
(3)是否存在實(shí)數(shù)m,使函數(shù)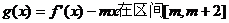 上有最小值-5?若
上有最小值-5?若
存在,請求出實(shí)數(shù)m的值;若不存在,請說明理由.
解:(1)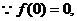
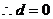

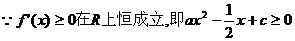 恒成立
恒成立
即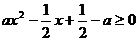 恒成立
恒成立
顯然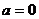 時(shí),上式不能恒成立
時(shí),上式不能恒成立
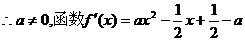 是二次函數(shù)
是二次函數(shù)
由于對一切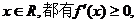 于是由二次函數(shù)的性質(zhì)可得
于是由二次函數(shù)的性質(zhì)可得
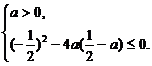 即
即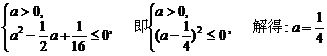
 .
.
(2)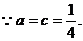
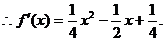
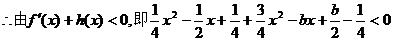
即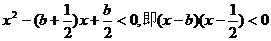
當(dāng)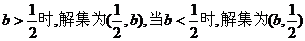 ,當(dāng)
,當(dāng)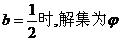 .
.
(3)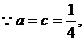
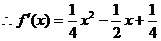
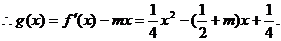
該函數(shù)圖象開口向上,且對稱軸為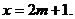
假設(shè)存在實(shí)數(shù)m使函數(shù) 區(qū)間
區(qū)間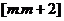 上有
上有
最小值-5.
①當(dāng)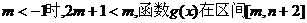 上是遞增的.
上是遞增的.
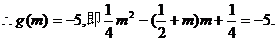
解得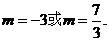

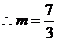 舍去
舍去
②當(dāng)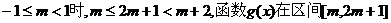 上是遞減的,而在
上是遞減的,而在
區(qū)間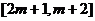 上是遞增的,
上是遞增的,
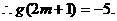
即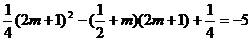
解得
③當(dāng)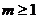 時(shí),
時(shí),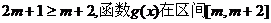 上遞減的
上遞減的
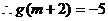
即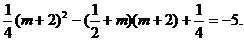
解得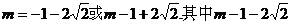 應(yīng)舍去.
應(yīng)舍去.
綜上可得,當(dāng)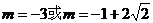 時(shí),
時(shí),
函數(shù)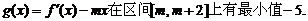
19.?dāng)?shù)列{an}滿足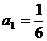 ,前n項(xiàng)和
,前n項(xiàng)和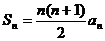 ,
,
(1)寫出
(2)猜出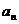 ,并用數(shù)學(xué)歸納法證明。
,并用數(shù)學(xué)歸納法證明。
解:(1)由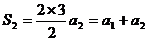 得:
得: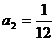
由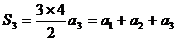 得:
得: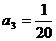
由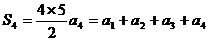 得:
得: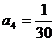
(2)猜想: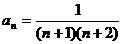
證明:①當(dāng)n=1時(shí),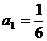 ,
,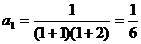 ,等式成立。
,等式成立。
②假設(shè)當(dāng)n=k時(shí)等式成立,則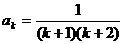 ,當(dāng)n=k+1時(shí),
,當(dāng)n=k+1時(shí),
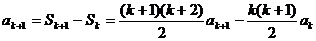

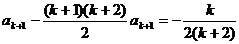
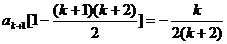
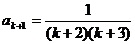 ,綜合①②,等式成立。
,綜合①②,等式成立。
17.一個(gè)均勻的正四面體的四個(gè)面上分別涂有1,2,3,4四個(gè)數(shù)字,現(xiàn)隨機(jī)投擲兩次,正四面體面朝下的數(shù)字分別為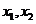 ,記
,記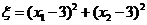 .
.
(1)分別求出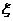 取得最大值和最小值時(shí)的概率;
取得最大值和最小值時(shí)的概率;
(2)求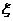 的分布列及數(shù)學(xué)期望.
的分布列及數(shù)學(xué)期望.
解:(1)擲出點(diǎn)數(shù)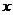 可能是:
可能是: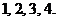
則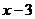 分別得:
分別得: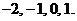 于是
于是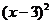 的所有取值分別為:
的所有取值分別為: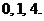
因此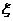 的所有取值為:0,1,2,4,5,8.
的所有取值為:0,1,2,4,5,8.
當(dāng)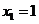 且
且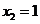 時(shí),
時(shí),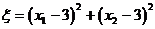 可取得最大值
可取得最大值 ,
,
此時(shí),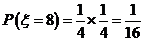 ;
;
當(dāng)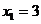 且
且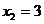 時(shí),
時(shí),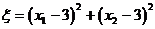 可取得最小值
可取得最小值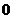 .
.
此時(shí),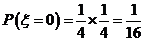 .
.
(2)由(Ⅰ)知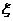 的所有取值為:0,1,2,4,5,8.
的所有取值為:0,1,2,4,5,8.
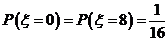 ;
;
當(dāng)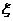 =1時(shí),
=1時(shí),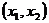 的所有取值為(2,3)、(4,3)、(3,2)、(3,4).即
的所有取值為(2,3)、(4,3)、(3,2)、(3,4).即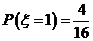 ;
;
當(dāng)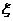 =2時(shí),
=2時(shí),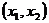 的所有取值為(2,2)、(4,4)、(4,2)、(2,4).
的所有取值為(2,2)、(4,4)、(4,2)、(2,4).
即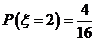 ;
;
當(dāng)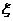 =4時(shí),
=4時(shí),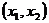 的所有取值為(1,3)、(3,1).即
的所有取值為(1,3)、(3,1).即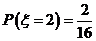 ;
;
當(dāng)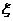 =5時(shí),
=5時(shí),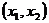 的所有取值為(2,1)、(1,4)、(1,2)、(4,1).即
的所有取值為(2,1)、(1,4)、(1,2)、(4,1).即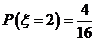 .
.
所以ξ的分布列為:
|
ξ |
0 |
1 |
2 |
4 |
5 |
8 |
|
P |
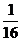 |
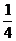 |
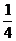 |
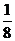 |
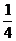 |
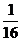 |
18
已知函數(shù)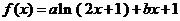 .
.
(Ⅰ)若函數(shù)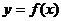 在
在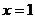 處取得極值,且曲線
處取得極值,且曲線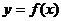 在點(diǎn)
在點(diǎn)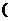
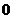 ,
,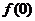
 處的切線與直線
處的切線與直線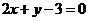 平行,求
平行,求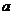 的值;
的值;
(Ⅱ)若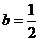 ,試討論函數(shù)
,試討論函數(shù)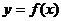 的單調(diào)性.
的單調(diào)性.
解:(Ⅰ)函數(shù)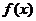 的定義域?yàn)?sub>
的定義域?yàn)?sub>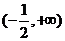 .
.

由題意 ,解得
,解得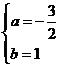
 .
.
(Ⅱ)若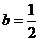 , 則
, 則 .
.
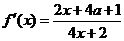 .
.
(1)令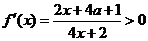 ,由函數(shù)定義域可知,
,由函數(shù)定義域可知,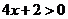 ,所以
,所以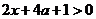
①當(dāng)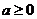 時(shí),
時(shí),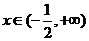 ,
,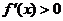 ,函數(shù)
,函數(shù)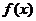 單調(diào)遞增;
單調(diào)遞增;
②當(dāng) 時(shí),
時(shí),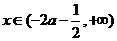 ,
,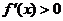 ,函數(shù)
,函數(shù)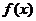 單調(diào)遞增;
單調(diào)遞增;
(2)令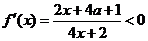 ,即
,即
①當(dāng)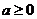 時(shí),不等式
時(shí),不等式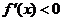 無解;
無解;
②當(dāng) 時(shí),
時(shí),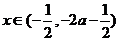 ,
,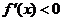 ,函數(shù)
,函數(shù)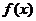 單調(diào)遞減;
單調(diào)遞減;
綜上:當(dāng)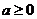 時(shí),函數(shù)
時(shí),函數(shù)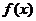 在區(qū)間
在區(qū)間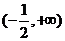 為增函數(shù);
為增函數(shù);
當(dāng) 時(shí),函數(shù)
時(shí),函數(shù)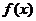 在區(qū)間
在區(qū)間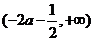 為增函數(shù);
為增函數(shù);
在區(qū)間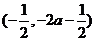 為減函數(shù).
為減函數(shù).
16.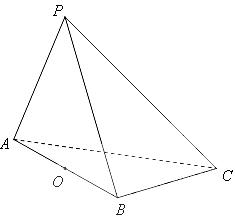 在三棱錐
在三棱錐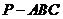 中,
中,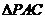 和
和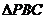 是邊長為
是邊長為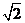 的等邊三角形,
的等邊三角形,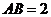 ,
,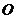 是
是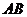 中點(diǎn).
中點(diǎn).
(Ⅰ)在棱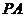 上求一點(diǎn)
上求一點(diǎn)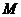 ,使得
,使得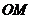 ∥平面
∥平面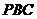 ;
;
(Ⅱ)求證:平面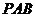 ⊥平面
⊥平面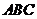 ;
;
(Ⅲ)求二面角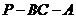 的余弦值.
的余弦值.
解
(Ⅰ)當(dāng)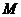 為棱
為棱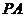 中點(diǎn)時(shí),
中點(diǎn)時(shí),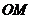 ∥平面
∥平面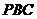 .
.
證明如下:
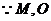 分別為
分別為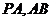 中點(diǎn),
中點(diǎn),
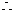
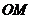 ∥
∥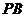
又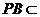 平面
平面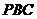 ,
,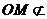 平面
平面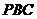
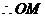 ∥平面
∥平面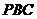 .
.
(Ⅱ)連結(jié)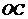 ,
,
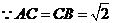 ,
, 為
為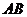 中點(diǎn),
中點(diǎn),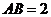 ,
,
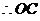 ⊥
⊥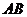 ,
,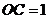 .
.
同理, 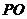 ⊥
⊥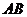 ,
,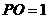 .
.
 又
又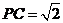 ,
,
 ,
,
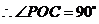 .
.
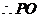 ⊥
⊥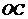 .
.
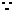
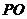 ⊥
⊥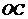 ,
,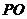 ⊥
⊥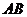 ,
,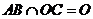 ,
,
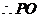 ⊥平面
⊥平面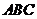 .
.
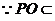 平面
平面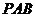
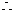 平面
平面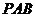 ⊥平面
⊥平面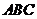 .
.
(Ⅲ)如圖,建立空間直角坐標(biāo)系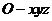 .
.
則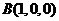 ,
,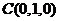 ,
,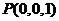 ,
,
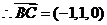 ,
,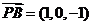 .
.
由(Ⅱ)知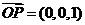 是平面
是平面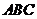
的一個(gè)法向量.
設(shè)平面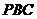 的法向量為
的法向量為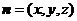 ,
,
則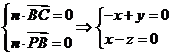 .
.
令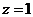 ,則
,則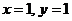 ,
,
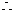 平面
平面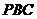 的一個(gè)法向量
的一個(gè)法向量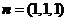 .
.
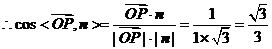 .
.
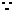 二面角
二面角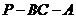 的平面角為銳角,
的平面角為銳角,
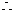 所求二面角
所求二面角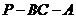 的余弦值為
的余弦值為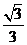 .
.
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com