
【題目】如圖所示,四棱錐![]() 中,四邊形
中,四邊形![]() 是直角梯形,
是直角梯形, ![]() 底面
底面![]() ,
, ![]() 為
為![]() 的中點,
的中點, ![]() 點在
點在![]() 上,且
上,且![]() .
.
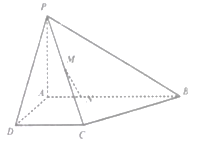
(1)證明: ![]() 平面
平面![]() ;
;
(2)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(I)見解析;(II)![]() ,
,
【解析】試題分析:(1)要證MN∥平面PAD,只需在面PAD內(nèi)找到一條直線和MN平行即可,而根據(jù)條件,易作輔助線過M作ME∥CD交PD于E,連接AE,下證MN∥AE;
(2)求直線MN與平面PCB所成的角,關(guān)鍵找直線MN在平面PCB內(nèi)的射影,而根據(jù)條件,易作輔助線過N點作NQ∥AP交BP于點Q,NF⊥CB交CB于點F,連接QF,過N點作NH⊥QF交QF于H,連接MH,下證NH⊥平面PBC,∴∠NMH為直線MN與平面PCB所成的角.解△MNH即可.
試題解析:
(1)過點![]() 作
作![]() 交
交![]() 于
于![]() 點,連結(jié)
點,連結(jié)![]() ,
,
![]() , 又
, 又![]()
![]() 為平行四邊形,
為平行四邊形, ![]() 平面
平面![]() .
.
(2)過![]() 點作
點作![]() 交
交![]() 于點
于點![]() ,
,![]() 于點
于點![]() ,
,
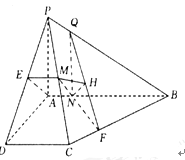
連結(jié)![]() ,過
,過![]() 點作
點作![]() 于
于![]() ,連結(jié)
,連結(jié)![]()
易知![]() 面
面![]() 而
而![]() 面
面![]() ,
,![]()
而![]() 面
面![]() ,
, ![]() 為直線
為直線![]() 與平面
與平面![]() 所成角,
所成角,
![]() 通過計算可得
通過計算可得![]() ,
,
 ,
,
![]() ,
,
![]() 直線
直線![]() 與平面
與平面![]() 所成角為
所成角為![]() .
.


 名校課堂系列答案
名校課堂系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某工廠為了對新研發(fā)的一種產(chǎn)品進(jìn)行合理定價,將該定價按事先擬定的價格進(jìn)行試銷,得到如下數(shù)據(jù):
單價 | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
銷量 | 90 | 84 | 83 | 80 | 75 | 68 |
(1)求回歸直線方程![]() ;
;
(2)預(yù)計在今后的銷售中,銷量與單價仍然服從(1)中的關(guān)系,且該產(chǎn)品的成本是4元/件,為使工廠獲得最大利潤,該產(chǎn)品的單價應(yīng)定為多少元?
附:  .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】隨著互聯(lián)網(wǎng)的發(fā)展,移動支付(又稱手機(jī)支付)越來越普通,某學(xué)校興趣小組為了了解移動支付在大眾中的熟知度,對15-65歲的人群隨機(jī)抽樣調(diào)查,調(diào)查的問題是“你會使用移動支付嗎?”其中,回答“會”的共有![]() 個人.把這
個人.把這![]() 個人按照年齡分成5組:第1組
個人按照年齡分成5組:第1組![]() ,第2組
,第2組![]() ,第3組
,第3組![]() ,第4組
,第4組![]() ,第5組
,第5組![]() ,然后繪制成如圖所示的頻率分布直方圖.其中,第一組的頻數(shù)為20.
,然后繪制成如圖所示的頻率分布直方圖.其中,第一組的頻數(shù)為20.
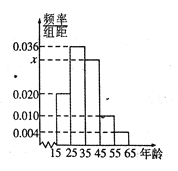
(1)求![]() 和
和![]() 的值,并根據(jù)頻率分布直方圖估計這組數(shù)據(jù)的眾數(shù);
的值,并根據(jù)頻率分布直方圖估計這組數(shù)據(jù)的眾數(shù);
(2)從第1,3,4組中用分層抽樣的方法抽取6人,求第1,3,4組抽取的人數(shù);
(3)在(2)抽取的6人中再隨機(jī)抽取2人,求所抽取的2人來自同一個組的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某企業(yè)實行裁員增效,已知現(xiàn)有員工![]() 人,每人每年可創(chuàng)純收益(已扣工資等)1萬元,據(jù)評估,在生產(chǎn)條件不變的情況下,每裁員一人,則留崗員工每人每年可多創(chuàng)收0.01萬元,但每年需付給下崗工人每位0.4萬元的生活費(fèi),并且企業(yè)正常運(yùn)轉(zhuǎn)所需人數(shù)不得少于現(xiàn)有員工的
人,每人每年可創(chuàng)純收益(已扣工資等)1萬元,據(jù)評估,在生產(chǎn)條件不變的情況下,每裁員一人,則留崗員工每人每年可多創(chuàng)收0.01萬元,但每年需付給下崗工人每位0.4萬元的生活費(fèi),并且企業(yè)正常運(yùn)轉(zhuǎn)所需人數(shù)不得少于現(xiàn)有員工的![]() ,設(shè)該企業(yè)裁員
,設(shè)該企業(yè)裁員![]() 人后,年純收益為
人后,年純收益為![]() 萬元.
萬元.
(1)寫出![]() 關(guān)于
關(guān)于![]() 的函數(shù)關(guān)系式,并指出
的函數(shù)關(guān)系式,并指出![]() 的取值范圍;
的取值范圍;
(2)當(dāng)![]() 時,該企業(yè)應(yīng)裁員多少人,才能獲得最大的經(jīng)濟(jì)效益(注:在保證能取得最大的經(jīng)濟(jì)效益的情況下,能少裁員,應(yīng)盡量少裁員)?
時,該企業(yè)應(yīng)裁員多少人,才能獲得最大的經(jīng)濟(jì)效益(注:在保證能取得最大的經(jīng)濟(jì)效益的情況下,能少裁員,應(yīng)盡量少裁員)?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知四棱柱![]() 的底面是邊長為
的底面是邊長為![]() 的菱形,且
的菱形,且![]() ,
,![]() 平面
平面![]() ,
,![]() ,設(shè)
,設(shè)![]() 為
為![]() 的中點
的中點
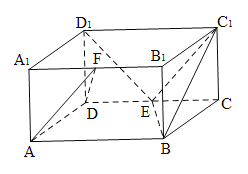
(1)求證:![]() 平面
平面![]()
(2)點![]() 在線段
在線段![]() 上,且
上,且![]() 平面
平面![]() ,求平面
,求平面![]() 和平面
和平面![]() 所成銳角的余弦值.
所成銳角的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知等比數(shù)列![]() 滿足
滿足![]() ,數(shù)列
,數(shù)列![]() 滿足
滿足![]() .
.
(1)求數(shù)列![]() ,
, ![]() 的通項公式;
的通項公式;
(2)令![]() ,求數(shù)列
,求數(shù)列![]() 的前
的前![]() 項和
項和![]() ;
;
(3)若![]() ,求對所有的正整數(shù)
,求對所有的正整數(shù)![]() 都有
都有![]() 成立的
成立的![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】過點![]() 作一直線與拋物線
作一直線與拋物線![]() 交于
交于![]() ,
,![]() 兩點,點
兩點,點![]() 是拋物線
是拋物線![]() 上到直線
上到直線![]() 的距離最小的點,直線
的距離最小的點,直線![]() 與直線
與直線![]() 交于點
交于點![]() .
.

(Ⅰ)求點![]() 的坐標(biāo);
的坐標(biāo);
(Ⅱ)求證:直線![]() 平行于拋物線的對稱軸.
平行于拋物線的對稱軸.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】一臺機(jī)器由于使用時間較長,生產(chǎn)的零件有一些會有缺損,按不同轉(zhuǎn)速生產(chǎn)出來的零件有缺損的統(tǒng)計數(shù)據(jù)如表所示:

(1)作出散點圖;
(2)如果![]() 與
與![]() 線性相關(guān),求出回歸直線方程.
線性相關(guān),求出回歸直線方程.
(3)若實際生產(chǎn)中,允許每小時的產(chǎn)品中有缺損的零件最多為10個,那么,機(jī)器的運(yùn)轉(zhuǎn)速度應(yīng)控制在什么范圍內(nèi)?
附:對于一組數(shù)據(jù)![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為,
的斜率和截距的最小二乘估計分別為,
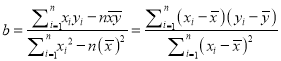 ,
, ![]()
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com