
【題目】已知函數f(x)是一次函數,g(x)是反比例函數,且滿足f[f(x)]=x+2,g(1)=﹣1
(1)求函數f(x)和g(x);
(2)設h(x)=f(x)+g(x),判斷函數h(x)在(0,+∞)上的單調性,并用定義加以證明.
【答案】
(1)解:因為f(x)是一次函數,g(x)是反比例函數
∴設f(x)=ax+b(a≠0),g(x)= ![]() (k≠0),
(k≠0),
∵f[f(x)]=x+2,
∴a(ax+b)+b=x+2,
∴a2x+(a+1)b=x+2,
∴ ![]() ,解得:a=1,b=1,
,解得:a=1,b=1,
故f(x)=x+1;
∵g(1)=﹣1,故k=﹣1,
故g(x)=﹣ ![]()
(2)解:判斷:函數h(x)在(0,+∞)上是增函數,
由(1)知h(x)= ![]() +1,設x1,x2是(0,+∞)上的任意兩個實數,且x1<x2,
+1,設x1,x2是(0,+∞)上的任意兩個實數,且x1<x2,
h(x1)﹣h(x2)=(x1﹣ ![]() )﹣(x2﹣
)﹣(x2﹣ ![]() )=(x1﹣x2)(1+
)=(x1﹣x2)(1+ ![]() ),
),
∵0<x1<x2,∴x1﹣x2<0,x1x2>0,
∴h(x1)﹣h(x2)<0,即h(x1)<h(x2),
∴函數h(x)在(0,+∞)遞增
【解析】(1)設出函數的解析式,通過待定系數法求出函數的解析式即可;(2)求出h(x)的解析式,根據函數單調性的定義判斷函數的單調性即可.
【考點精析】本題主要考查了函數單調性的判斷方法的相關知識點,需要掌握單調性的判定法:①設x1,x2是所研究區間內任兩個自變量,且x1<x2;②判定f(x1)與f(x2)的大小;③作差比較或作商比較才能正確解答此題.


科目:高中數學 來源: 題型:
【題目】如圖,半徑為1,圓心角為 ![]() 的圓弧
的圓弧 ![]() 上有一點C.
上有一點C. 
(1)若C為圓弧AB的中點,點D在線段OA上運動,求| ![]() +
+ ![]() |的最小值;
|的最小值;
(2)若D,E分別為線段OA,OB的中點,當C在圓弧 ![]() 上運動時,求
上運動時,求 ![]()
![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數y=f(x)對任意的x∈(﹣ ![]() ,
, ![]() )滿足f′(x)cosx+f(x)sinx>0(其中f′(x)是函數f(x)的導函數),則下列不等式成立的是( )
)滿足f′(x)cosx+f(x)sinx>0(其中f′(x)是函數f(x)的導函數),則下列不等式成立的是( )
A.![]() f(﹣
f(﹣ ![]() )<f(﹣
)<f(﹣ ![]() )
)
B.![]() f(
f( ![]() )<f(
)<f( ![]() )??
)??
C.f(0)>2f( ![]() )
)
D.f(0)> ![]() f(
f( ![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某同學在獨立完成課本上的例題:“求證: ![]() +
+ ![]() <2
<2 ![]() ”后,又進行了探究,發現下面的不等式均成立.
”后,又進行了探究,發現下面的不等式均成立. ![]() +
+ ![]() <2
<2 ![]()
![]() +
+ ![]() <2
<2 ![]()
![]() +
+ ![]() <2
<2 ![]()
![]() +
+ ![]() <2
<2 ![]() ,
,![]() +
+ ![]() ≤2
≤2 ![]() .
.
(1)請根據上述不等式歸納出一個一般性的不等式;(用字母表示)
(2)請用合適的方法證明你寫出的不等式成立.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知向量m=(3sinx,cosx),n=(-cosx,![]() cosx),f(x)=m·n-
cosx),f(x)=m·n-![]() .
.
(1)求函數f(x)的最大值及取得最大值時x的值;
(2)若方程f(x)=a在區間![]() 上有兩個不同的實數根,求實數a的取值范圍.
上有兩個不同的實數根,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義在[﹣1,1]的函數f(x)滿足下列兩個條件:①任意的x∈[﹣1,1],都有f(﹣x)=﹣f(x);②任意的m,n∈[0,1],當m≠n,都有 ![]() <0,則不等式f(1﹣3x)<f(x﹣1)的解集是( )
<0,則不等式f(1﹣3x)<f(x﹣1)的解集是( )
A.[0, ![]() )
)
B.( ![]() ,
, ![]() ]
]
C.[﹣1, ![]() )
)
D.[ ![]() ,1]
,1]
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設f(x)=ax3+bx2+cx的極小值為﹣8,其導函數y=f′(x)的圖象經過點 ![]() ,如圖所示,
,如圖所示, 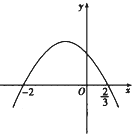
(1)求f(x)的解析式;
(2)若對x∈[﹣3,3]都有f(x)≥m2﹣14m恒成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于函數f(x)定義域中任意的x1 , x2(x1≠x2)有如下結論
1)f(x1+x2)=f(x1)f(x2)
2)f(x1x2)=f(x1)+f(x2)
3) ![]() >0
>0
4)f( ![]() )<
)< ![]()
5)f( ![]() )>
)> ![]()
6)f(﹣x)=f(x).
當f(x)=lgx時,上述結論正確的序號為 . (注:把你認為正確的命題的序號都填上).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com