
22.(1)證明:因為CB⊥平面A1B,所以A1C在平面A1B上的射影為A1B.
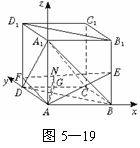
由A1B⊥AE,AE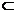 平面A1B,得A1C⊥AE.
平面A1B,得A1C⊥AE.
同理可證A1C⊥AF.
因為A1C⊥AF,A1C⊥AE,
 所以A1C⊥平面AEF.
所以A1C⊥平面AEF.
(2)解:過A作BD的垂線交CD于G,因為D1D⊥AG,所以AG⊥平面D1B1BD.
設AG與A1C所成的角為α,則α即為平面AEF與平面D1B1BD所成的角.
由已知,計算得DG=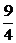 .
.
如圖5-19建立直角坐標系,則得點A(0,0,0),G(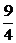 ,3,0),A1(0,0,5),
,3,0),A1(0,0,5),
C(4,3,0).
AG={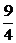 ,3,0},A1C={4,3,-5}.
,3,0},A1C={4,3,-5}.
因為AG與A1C所成的角為α,
所以cosα=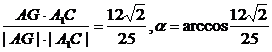 .
.
由定理知,平面AEF與平面D1B1BD所成角的大小為arccos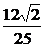 .
.
注:沒有學習向量知識的同學可用以下的方法求二面角的平面角.
解法一:設AG與BD交于M,則AM⊥面BB1D1D,再作AN⊥EF交EF于N,連接MN,則∠ANM即為面AEF與D1B1BD所成的角α,用平面幾何的知識可求出AM、AN的長度.
解法二:用面積射影定理cosα=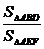 .
.
評述:立體幾何考查的重點有三個:一是空間線面位置關系的判定;二是角與距離的計算;三是多面體與旋轉體中的計算.
21.解:(1)由題意知B(a,a,0),C(-a,a,0),D(-a,-a,0),E( ).
).
由此得,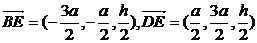
∴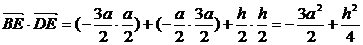 ,
,
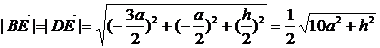 .
.
由向量的數量積公式有
cos<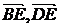 >=
>=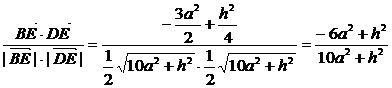
(2)若∠BED是二面角α-VC-β的平面角,則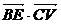 ,則有
,則有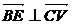 =0.
=0.
又由C(-a,a,0),V(0,0,h),有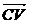 =(a,-a,h)且
=(a,-a,h)且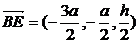 ,
,
∴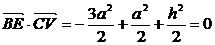 .
.
即h= a,這時有
a,這時有
cos<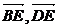 >=
>=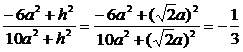 ,
,
∴∠BED=<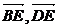 >=arccos(
>=arccos(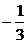 )=π-arccos
)=π-arccos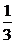
評述:本小題主要考查空間直角坐標的概念、空間點和向量的坐標表示以及兩個向量夾角的計算方法;考查運用向量研究空間圖形的數學思想方法.
20.解:(1)記P(x,y),由M(-1,0),N(1,0)得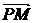 =-
=-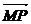 =(-1-x,-y),
=(-1-x,-y),
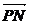 =-
=-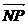 =(1-x,-y),
=(1-x,-y),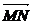 =-
=-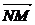 =(2,0)
=(2,0)
∴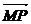 ·
·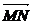 =2(1+x),
=2(1+x),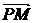 ·
·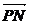 =x2+y2-1,
=x2+y2-1,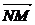 ·
·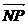 =2(1-x).
=2(1-x).
于是,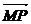 ·
·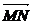 ,
,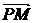 ·
·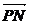 ,
,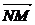 ·
·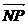 是公差小于零的等差數列等價于
是公差小于零的等差數列等價于

即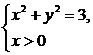
所以,點P的軌跡是以原點為圓心,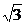 為半徑的右半圓.
為半徑的右半圓.
(2)點P的坐標為(x0,y0).
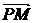 ·
·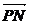 =x02+y02-1=2.
=x02+y02-1=2.
|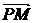 |·|
|·|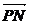 |=
|= .
.
∴cosθ=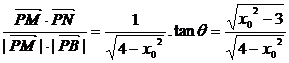
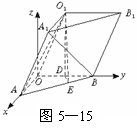
19.解:(1)如圖5-18,以點A為坐標原點O,以AB所在直線為Oy軸,以AA1所在直線為Oz軸,以經過原點且與平面ABB1A1垂直的直線為Ox軸,建立空間直角坐標系.
由已知,得
A(0,0,0),B(0,a,0),A1(0,0, a),C1(
a),C1(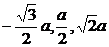 ).
).
(2)坐標系如圖,取A1B1的中點M,于是有M(0,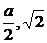 a),連AM,MC1有
a),連AM,MC1有
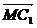 =(-
=(-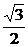 a,0,0),且
a,0,0),且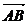 =(0,a,0),
=(0,a,0),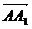 =(0,0,
=(0,0, a)
a)
由于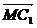 ·
·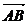 =0,
=0,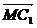 ·
·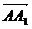 =0,所以MC1⊥面ABB1A1.
=0,所以MC1⊥面ABB1A1.
∴AC1與AM所成的角就是AC1與側面ABB1A1所成的角.
∵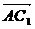 =(
=(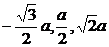 ),
),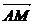 =(0,
=(0,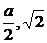 a),
a),
∴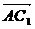 ·
·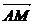 =0+
=0+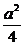 +2a2=
+2a2=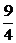 a2.
a2.
而|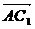 |=
|=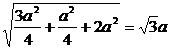 .
.
|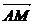 |=
|=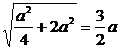 .
.
∴cos<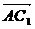 ,
,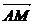 >=
>=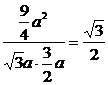 .
.
所以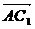 與
與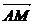 所成的角,即AC1與側面ABB1A1所成的角為30°.
所成的角,即AC1與側面ABB1A1所成的角為30°.
18.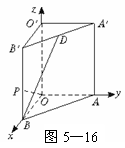 解法一:如圖5-16,以O點為原點建立空間直角坐標系.
解法一:如圖5-16,以O點為原點建立空間直角坐標系.
由題意,有B(3,0,0),D(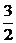 ,2,4),設P(3,0,z),則
,2,4),設P(3,0,z),則
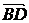 ={-
={-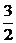 ,2,4},
,2,4},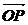 ={3,0,z}.
={3,0,z}.
∵BD⊥OP,∴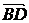 ·
·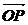 =-
=-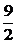 +4z=0,z=
+4z=0,z=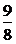 .
.
∵BB′⊥平面AOB,∴∠POB是OP與底面AOB所成的角.
tanPOB=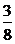 ,∴∠POB=arctan
,∴∠POB=arctan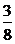 .
.
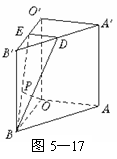 解法二:取O′B′中點E,連結DE、BE,如圖5-17,則
解法二:取O′B′中點E,連結DE、BE,如圖5-17,則
DE⊥平面OBB′O′,
∴BE是BD在平面OBB′O′內的射影.
又∵OP⊥BD.
由三垂線定理的逆定理,得OP⊥BE.
在矩形OBB′O′中,易得Rt△OBP∽Rt△BB′E,
∴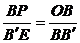 ,得BP=
,得BP=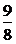 .
.
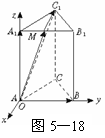 (以下同解法一)
(以下同解法一)
17. 解:(1)取OB的中點D,連結O1D,
解:(1)取OB的中點D,連結O1D,
則O1D⊥OB.
∵平面OBB1O1⊥平面OAB,
∴O1D⊥平面OAB.
過D作AB的垂線,垂足為E,連結O1E.
則O1E⊥AB.
∴∠DEO1為二面角O1-AB-O的平面角.
由題設得O1D=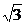 ,
,
sinOBA=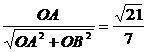 ,
,
∴DE=DBsinOBA=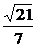
∵在Rt△O1DE中,tanDEO1=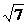 ,
,
∴∠DEO1=arctan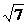 ,即二面角O1-AB-O的大小為arctan
,即二面角O1-AB-O的大小為arctan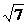 .
.
(2)以O點為原點,分別以OA、OB所在直線為x、y軸,過O點且與平面AOB垂直的直線為z軸,建立空間直角坐標系如圖5-15.則
O(0,0,0),O1(0,1,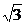 ),A(
),A(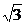 ,0,0),A1(
,0,0),A1(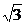 ,1,
,1,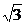 ),B(0,2,0).
),B(0,2,0).
設異面直線A1B與AO1所成的角為α,
則 ,
,
cosα=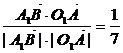 ,
,
∴異面直線A1B與AO1所成角的大小為arccos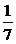 .
.
16.(1)證明:∵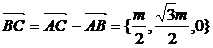 ,∴|
,∴| 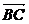 |=m,
|=m,
又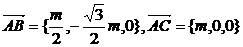
∴|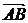 |=m,|
|=m,|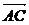 |=m,∴△ABC為正三角形.
|=m,∴△ABC為正三角形.
又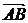 ·
·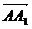 =0,即AA1⊥AB,同理AA1⊥AC,∴AA1⊥平面ABC,從而三棱柱ABC-A1B1C1是正三棱柱.
=0,即AA1⊥AB,同理AA1⊥AC,∴AA1⊥平面ABC,從而三棱柱ABC-A1B1C1是正三棱柱.
(2)解:取AB中點O,連結CO、A1O.
∵CO⊥AB,平面ABC⊥平面ABB1A1,∴CO⊥平面ABB1A1,即∠CA1O為直線CA1與平面A1ABB1所成的角.
在Rt△CA1O中,CO=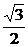 m,CA1=
m,CA1=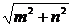 ,
,
∴sinCA1O=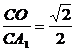 ,即∠CA1O=45°.
,即∠CA1O=45°.
15.答案:(4,2)
解析:設P(x,y),由定比分點公式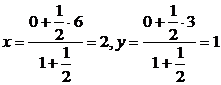 ,
,
則P(2,1),又由中點坐標公式,可得B(4,2).
14. 答案:-63
答案:-63
解析:解方程組
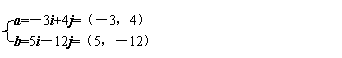
得
∴a·b=(-3)×5+4×(-12)=-63.
評述:本題考查平面向量數量積的坐標表示及求法.
13.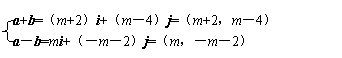 答案:-2
答案:-2
解析:由題意,得
∵(a+b)⊥(a-b),∴(m+2)×m+(m-4)(-m-2)=0,∴m=-2.
評述:本題考查平面向量的加、減法,平面向量的數量積及運算,兩向量垂直的充要條件.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com