影音先锋制服丝袜_欧美 国产 日本_亚洲欧美综合自拍_亚洲最大成人在线观看_成人一区二区三_色呦呦网站入口_亚洲欧美高清在线_黄页网站在线看_一卡二卡在线观看_在线观看免费黄网站

已知正數a，b，c滿足a+b+c=1證明  a3+b3+c3≥

a2+b2+c2

3

．

已知二次函數 f(x)=ax²+bx+c(a、b、c∈R)滿足f(1)=1且f(-1)=0,對于任意實數x,都有f(x)≥x.

(1)證明a＞0,c＞0；

(2)設函數g(x)=f(x)-mx(x∈R),求m的取值范圍,使函數g(x)在區間［-1,1］上是單調函數.

已知數列{a_n},a₁=2a+1(a≠-1的常數),a_n=2a_n-1+n²-4n+2(n≥2,n∈N^∗),數列{b_n}的首項, b₁=a,b_n=a_n+n²(n≥2,n∈N^∗).

(1)證明:{b_n}從第2項起是以2為公比的等比數列并求{b_n}通項公式;

(2)設S_n為數列{b_n}的前n項和,且{S_n}是等比數列,求實數a的值;(3)當a>0時,求數列{a_n}的最小項.

 

如圖，圓柱OO內有一個三棱柱ＡＢＣ—Ａ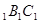，三棱柱的底面為圓柱底面的內接三角形，且AB是圓O直徑。

(1)證明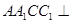：平面平面;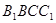

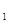
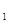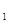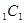
(2)設ＡＢ=ＡＡ,在圓柱ＯＯ內隨機選取一點，記該點取自三棱柱ＡＢＣ—ＡＢ內的概率為Ｐ.

①當點C在圓周上運動時，求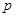的最大值；

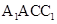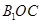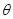
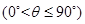②記平面與平面所成的角為，當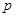取最大值時，求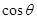的值。