
【題目】新高考3+3最大的特點就是取消文理科,除語文、數學、外語之外,從物理、化學、生物、政治、歷史、地理這6科中自由選擇三門科目作為選考科目.某研究機構為了了解學生對全理(選擇物理、化學、生物)的選擇是否與性別有關,覺得從某學校高一年級的650名學生中隨機抽取男生,女生各25人進行模擬選科.經統計,選擇全理的人數比不選全理的人數多10人.
(1)請完成下面的2×2列聯表;
選擇全理 | 不選擇全理 | 合計 | |
男生 | 5 | ||
女生 | |||
合計 |
(2)估計有多大把握認為選擇全理與性別有關,并說明理由;
(3)現從這50名學生中已經選取了男生3名,女生2名進行座談,從中抽取2名代表作問卷調查,求至少抽到一名女生的概率.
附: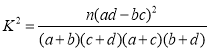 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.076 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 名師指導期末沖刺卷系列答案
名師指導期末沖刺卷系列答案 開心蛙口算題卡系列答案
開心蛙口算題卡系列答案科目:高中數學 來源: 題型:
【題目】在股票市場上,投資者常根據股價![]() 每股的價格
每股的價格![]() 走勢圖來操作,股民老張在研究某只股票時,發現其在平面直角坐標系內的走勢圖有如下特點:每日股價
走勢圖來操作,股民老張在研究某只股票時,發現其在平面直角坐標系內的走勢圖有如下特點:每日股價![]() 元
元![]() 與時間
與時間![]() 天
天![]() 的關系在ABC段可近似地用函數
的關系在ABC段可近似地用函數![]() 的圖象從最高點A到最低點C的一段來描述
的圖象從最高點A到最低點C的一段來描述![]() 如圖
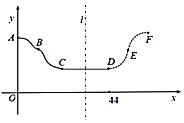
如圖![]() ,并且從C點到今天的D點在底部橫盤整理,今天也出現了明顯的底部結束信號.老張預測這只股票未來一段時間的走勢圖會如圖中虛線DEF段所示,且DEF段與ABC段關于直線l:
,并且從C點到今天的D點在底部橫盤整理,今天也出現了明顯的底部結束信號.老張預測這只股票未來一段時間的走勢圖會如圖中虛線DEF段所示,且DEF段與ABC段關于直線l:![]() 對稱,點B,D的坐標分別是
對稱,點B,D的坐標分別是![]() .
.
![]() 請你幫老張確定a,
請你幫老張確定a,![]() ,
,![]() 的值,并寫出ABC段的函數解析式;
的值,并寫出ABC段的函數解析式;
![]() 如果老張預測準確,且今天買入該只股票,那么買入多少天后股價至少是買入價的兩倍?
如果老張預測準確,且今天買入該只股票,那么買入多少天后股價至少是買入價的兩倍?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某小組有7個同學,其中4個同學從來沒有參加過天文研究性學習活動,3個同學曾經參加過天文研究性學習活動.
(1)現從該小組中隨機選2個同學參加天文研究性學習活動,求恰好選到1個曾經參加過天文研究性學習活動的同學的概率;
(2)若從該小組隨機選2個同學參加天文研究性學習活動,則活動結束后,該小組有參加過天文研究性學習活動的同學個數![]() 是一個隨機變量,求隨機變量
是一個隨機變量,求隨機變量![]() 的分布列和數學期望
的分布列和數學期望![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,曲線C的參數方程是![]() (
(![]() 為參數),把曲線C的橫坐標縮短為原來的
為參數),把曲線C的橫坐標縮短為原來的![]() ,縱坐標縮短為原來的一半,得到曲線
,縱坐標縮短為原來的一半,得到曲線![]() 直線l的普通方程是
直線l的普通方程是![]() ,以坐標原點O為極點,x軸正半軸為極軸建立極坐標系.
,以坐標原點O為極點,x軸正半軸為極軸建立極坐標系.
(1)求直線l的極坐標方程和曲線![]() 的普通方程;
的普通方程;
(2)記射線![]() (
(![]() )與
)與![]() 交于點A,與l交于點B,求
交于點A,與l交于點B,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為踐行“綠水青山就是金山銀山”的發展理念,某城區對轄區內![]() ,
,![]() ,
,![]() 三類行業共200個單位的生態環境治理成效進行了考核評估,考評分數達到80分及其以上的單位被稱為“星級”環保單位,未達到80分的單位被稱為“非星級”環保單位.現通過分層抽樣的方法獲得了這三類行業的20個單位,其考評分數如下:
三類行業共200個單位的生態環境治理成效進行了考核評估,考評分數達到80分及其以上的單位被稱為“星級”環保單位,未達到80分的單位被稱為“非星級”環保單位.現通過分層抽樣的方法獲得了這三類行業的20個單位,其考評分數如下:
![]() 類行業:85,82,77,78,83,87;
類行業:85,82,77,78,83,87;
![]() 類行業:76,67,80,85,79,81;
類行業:76,67,80,85,79,81;
![]() 類行業:87,89,76,86,75,84,90,82.
類行業:87,89,76,86,75,84,90,82.
(Ⅰ)計算該城區這三類行業中每類行業的單位個數;
(Ⅱ)若從抽取的![]() 類行業這6個單位中,再隨機選取3個單位進行某項調查,求選出的這3個單位中既有“星級”環保單位,又有“非星級”環保單位的概率.
類行業這6個單位中,再隨機選取3個單位進行某項調查,求選出的這3個單位中既有“星級”環保單位,又有“非星級”環保單位的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某闖關游戲共有兩關,游戲規則:先闖第一關,當第一關闖過后,才能進入第二關,兩關都闖過,則闖關成功,且每關各有兩次闖關機會.已知闖關者甲第一關每次闖過的概率均為![]() ,第二關每次闖過的概率均為
,第二關每次闖過的概率均為![]() .假設他不放棄每次闖關機會,且每次闖關互不影響.
.假設他不放棄每次闖關機會,且每次闖關互不影響.
(1)求甲恰好闖關3次才闖關成功的概率;
(2)記甲闖關的次數為![]() ,求隨機變量
,求隨機變量![]() 的分布列和期望.。
的分布列和期望.。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下面幾種推理是類比推理的( )
A. 兩條直線平行,同旁內角互補,如果![]() 和
和![]() 是兩條平行直線的同旁內角,則
是兩條平行直線的同旁內角,則![]()
B. 由平面三角形的性質,推測空間四邊形的性質
C. 某校高二級有20個班,1班有51位團員,2班有53位團員,3班有52位團員,由此可以推測各班都超過50位團員.
D. 一切偶數都能被2整除,![]() 是偶數,所以
是偶數,所以![]() 能被2整除.
能被2整除.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年某地區初中升學體育考試規定:考生必須參加長跑、擲實心球、1分鐘跳繩三項測試.某學校在九年級上學期開始,就為掌握全年級學生1分鐘跳繩情況,抽取了100名學生進行測試,得到下面的頻率分布直方圖.
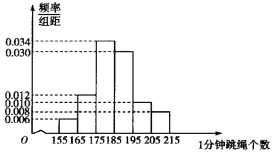
(Ⅰ)規定學生1分鐘跳繩個數大于等于185為優秀.若在抽取的100名學生中,女生共有50人,男生1分鐘跳繩個數大于等于185的有28人.根據已知條件完成下面的![]() 列聯表,并根據這100名學生的測試成績,判斷能否有99%的把握認為學生1分鐘跳繩成績是否優秀與性別有關.
列聯表,并根據這100名學生的測試成績,判斷能否有99%的把握認為學生1分鐘跳繩成績是否優秀與性別有關.
1分鐘跳繩成績 | 優秀 | 不優秀 | 合計 |
男生人數 | 28 | ||
女生人數 | 100 | ||
合計 | 100 |
(Ⅱ)根據往年經驗,該校九年級學生經過訓練,正式測試時每人1分鐘跳繩個數都有明顯進步.假設正式測試時每人1分鐘跳繩個數都比九年級上學期開始時增加10個,全年級恰有2000名學生,若所有學生的1分鐘跳繩個數![]() 服從正態分布
服從正態分布![]() ,用樣本數據的平均值和標準差估計
,用樣本數據的平均值和標準差估計![]() 和
和![]() ,各組數據用中點值代替),估計正式測試時1分鐘跳繩個數大于183的人數(結果四舍五入到整數
,各組數據用中點值代替),估計正式測試時1分鐘跳繩個數大于183的人數(結果四舍五入到整數
附: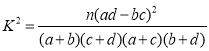 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
若隨機變量![]() 服從正態分布
服從正態分布![]() ,則
,則![]()
![]()
![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com