
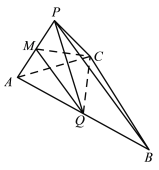
【題目】如圖,在三棱錐![]() 中,
中,![]() 為正三角形,
為正三角形,![]() 為棱
為棱![]() 的中點(diǎn),
的中點(diǎn),![]() ,
,![]() ,平面
,平面![]() 平面
平面![]()
(1)求證:平面![]() 平面
平面![]() ;
;
(2)若![]() 是棱
是棱![]() 上一點(diǎn),
上一點(diǎn),![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() ,求二面角
,求二面角![]() 的正弦值.
的正弦值.
【答案】(1)證明見解析(2)![]()
【解析】
(1)先根據(jù)平面![]() 平面
平面![]() ,得出
,得出![]() ,結(jié)合條件
,結(jié)合條件![]() 得出
得出![]() 平面
平面![]() ,從而可得.
,從而可得.
(2)建立空間直角坐標(biāo)系,結(jié)合![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() 得出
得出![]() 的坐標(biāo),然后利用法向量可求.
的坐標(biāo),然后利用法向量可求.
(1)因?yàn)?/span>![]() 為正三角形,
為正三角形,![]() 為棱
為棱![]() 的中點(diǎn),所以
的中點(diǎn),所以![]() ,
,
又平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
所以![]() ,又
,又![]() ,且
,且![]() ,
,
所以![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .
.
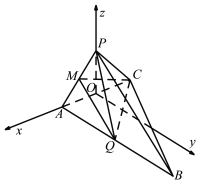
(2)作![]() 中點(diǎn)
中點(diǎn)![]() ,連
,連![]() ,由(1)及
,由(1)及![]() 可知
可知![]() 平面
平面![]() ,
,
以![]() 為坐標(biāo)原點(diǎn),
為坐標(biāo)原點(diǎn),![]() 分別為
分別為![]() 軸,過(guò)
軸,過(guò)![]() 且平行于
且平行于![]() 的方向?yàn)?/span>
的方向?yàn)?/span>![]() 軸,如圖,建立空間直角坐標(biāo)系.
軸,如圖,建立空間直角坐標(biāo)系.
設(shè)![]() ,
,
則![]() ,
,
![]() ,
,
設(shè)![]() ,則
,則![]() ,
,![]() ,
,
設(shè)平面![]() 的法向量為
的法向量為![]() ,
,
因?yàn)?/span>![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() ,
,
所以![]() ,即
,即![]() ,解得
,解得![]() ,
,
即![]() 為
為![]() 的中點(diǎn),則
的中點(diǎn),則![]()
設(shè)平面![]() 的法向量為
的法向量為![]() ,則
,則
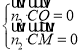 ,即
,即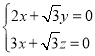 ,
,
取![]() .
.
設(shè)平面![]() 的法向量為
的法向量為![]() ,則
,則![]() ,
,
則二面角![]() 的余弦值為
的余弦值為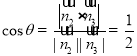 ,
,
故![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)![]() 為給定的不小于
為給定的不小于![]() 的正整數(shù),考察
的正整數(shù),考察![]() 個(gè)不同的正整數(shù)
個(gè)不同的正整數(shù)![]() ,
,![]() ,
,![]() ,
,![]() 構(gòu)成的集合
構(gòu)成的集合![]() ,若集合
,若集合![]() 的任何兩個(gè)不同的非空子集所含元素的總和均不相等,則稱集合
的任何兩個(gè)不同的非空子集所含元素的總和均不相等,則稱集合![]() 為“差異集合”.
為“差異集合”.
(1)分別判斷集合![]() ,集合
,集合![]() 是否是“差異集合”;(只需寫出結(jié)論)
是否是“差異集合”;(只需寫出結(jié)論)
(2)設(shè)集合![]() 是“差異集合”,記
是“差異集合”,記![]() ,求證:數(shù)列
,求證:數(shù)列![]() 的前
的前![]() 項(xiàng)和
項(xiàng)和![]()
![]() ;
;
(3)設(shè)集合![]() 是“差異集合”,求
是“差異集合”,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】第28屆金雞百花電影節(jié)將于11月19日至23日在福建省廈門市舉辦,近日首批影展片單揭曉,《南方車站的聚會(huì)》《春江水暖》《第一次的離別》《春潮》《抵達(dá)之謎》五部?jī)?yōu)秀作品將在電影節(jié)進(jìn)行展映.若從這五部作品中隨機(jī)選擇兩部放在展映的前兩位,則《春潮》與《抵達(dá)之謎》至少有一部被選中的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知點(diǎn)A(0,-2),橢圓E: ![]() (a>b>0)的離心率為
(a>b>0)的離心率為![]() ,F是橢圓E的右焦點(diǎn),直線AF的斜率為
,F是橢圓E的右焦點(diǎn),直線AF的斜率為![]() ,O為坐標(biāo)原點(diǎn).
,O為坐標(biāo)原點(diǎn).
(1)求E的方程;
(2)設(shè)過(guò)點(diǎn)A的動(dòng)直線l與E相交于P,Q兩點(diǎn).當(dāng)△OPQ的面積最大時(shí),求l的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知橢圓![]() :
:![]()
![]() 的離心率
的離心率![]() ,左、右焦點(diǎn)分別是
,左、右焦點(diǎn)分別是![]() 、
、![]() ,且橢圓上一動(dòng)點(diǎn)
,且橢圓上一動(dòng)點(diǎn)![]() 到
到![]() 的最遠(yuǎn)距離為
的最遠(yuǎn)距離為![]() ,過(guò)
,過(guò)![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
,![]() 兩點(diǎn).
兩點(diǎn).
(1)求橢圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(2)當(dāng)![]() 以
以![]() 為直角時(shí),求直線
為直角時(shí),求直線![]() 的方程;
的方程;
(3)直線![]() 的斜率存在且不為0時(shí),試問
的斜率存在且不為0時(shí),試問![]() 軸上是否存在一點(diǎn)
軸上是否存在一點(diǎn)![]() 使得
使得![]() ,若存在,求出
,若存在,求出![]() 點(diǎn)坐標(biāo);若不存在,請(qǐng)說(shuō)明理由.
點(diǎn)坐標(biāo);若不存在,請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】2019年雙十一落下帷幕,天貓交易額定格在268(單位:十億元)人民幣(下同),再創(chuàng)新高,比去年218(十億元)多了50(十億元),這些數(shù)字的背后,除了是消費(fèi)者買買買的表現(xiàn),更是購(gòu)物車?yán)镏袊?guó)新消費(fèi)的奇跡,為了研究歷年銷售額的變化趨勢(shì),一機(jī)構(gòu)統(tǒng)計(jì)了2010年到2019年天貓雙十一的銷售額數(shù)據(jù)![]() (單位:十億元).繪制如下表1:
(單位:十億元).繪制如下表1:
表1
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
編號(hào) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
銷售額 | 0.9 | 8.7 | 22.4 | 41 | 65 | 94 | 132.5 | 172.5 | 218 | 268 |
根據(jù)以上數(shù)據(jù)繪制散點(diǎn)圖,如圖所示.
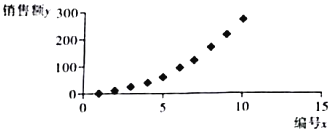
把銷售超過(guò)100(十億元)的年份叫“暢銷年”,把銷售額超過(guò)200(十億元)的年份叫“狂歡年”,從2010年到2019年這十年的“暢銷年”中任取2個(gè),求至少取到一個(gè)“狂歡年”的概率.
參考公式:對(duì)于一組數(shù)據(jù)![]() ,
,![]() ,…,
,…,![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計(jì)公式分別為
的斜率和截距的最小二乘估計(jì)公式分別為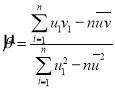 ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知![]() 的三個(gè)頂點(diǎn)
的三個(gè)頂點(diǎn)![]() 均在拋物線
均在拋物線![]() 上,給出下列命題:
上,給出下列命題:
①若直線![]() 過(guò)點(diǎn)
過(guò)點(diǎn)![]() ,則存在
,則存在![]() 使拋物線
使拋物線![]() 的焦點(diǎn)恰為
的焦點(diǎn)恰為![]() 的重心;
的重心;
②若直線![]() 過(guò)點(diǎn)
過(guò)點(diǎn)![]() ,則存在點(diǎn)
,則存在點(diǎn)![]() 使
使![]() 為直角三角形;
為直角三角形;
③存在![]() ,使拋物線
,使拋物線![]() 的焦點(diǎn)恰為
的焦點(diǎn)恰為![]() 的外心;
的外心;
④若邊![]() 的中線
的中線![]() 軸,
軸,![]() ,則
,則![]() 的面積為
的面積為![]() .
.
其中正確的序號(hào)為______________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】交強(qiáng)險(xiǎn)是車主必須為機(jī)動(dòng)車購(gòu)買的險(xiǎn)種,若普通6座以下私家車投保交強(qiáng)險(xiǎn)第一年的費(fèi)用(基準(zhǔn)保費(fèi))統(tǒng)一為a元,在下一年續(xù)保時(shí),實(shí)行的是費(fèi)率浮動(dòng)機(jī)制,保費(fèi)與上一年度車輛發(fā)生道路交通事故的情況相聯(lián)系,發(fā)生交通事故的次數(shù)越多,費(fèi)率也就越高,具體浮動(dòng)情況如下表:
交強(qiáng)險(xiǎn)浮動(dòng)因素和浮動(dòng)費(fèi)率比率表 | ||
浮動(dòng)因素 | 浮動(dòng)比率 | |
| 上一年度未發(fā)生有責(zé)任道路交通事故 | 下浮10% |
| 上兩年度未發(fā)生有責(zé)任道路交通事故 | 下浮 |
| 上三年度未發(fā)生有責(zé)任道路交通事故 | 下浮30% |
| 上一個(gè)年度發(fā)生一次有責(zé)任不涉及死亡的道路交通事故 | 0% |
| 上一個(gè)年度發(fā)生兩次及兩次以上有責(zé)任不涉及死亡的道路交通事故 | 上浮10% |
| 上一個(gè)年度發(fā)生有責(zé)任交通死亡事故 | 上浮30% |
某機(jī)構(gòu)為了解某一品牌普通6座以下私家車的投保情況,隨機(jī)抽取了
類型 | A1 | A2 | A3 | A4 | A5 | A6 |
數(shù)量 | 10 | 5 | 5 | 20 | 15 | 5 |
以這60輛該品牌車的投保類型的頻率代替一輛車投保類型的概率,完成下列問題:
(1)按照我國(guó)《機(jī)動(dòng)車交通事故責(zé)任強(qiáng)制保險(xiǎn)條例》汽車交強(qiáng)險(xiǎn)價(jià)格的規(guī)定,![]() ,記
,記![]() 為某同學(xué)家的一輛該品牌車在第四年續(xù)保時(shí)的費(fèi)用,求
為某同學(xué)家的一輛該品牌車在第四年續(xù)保時(shí)的費(fèi)用,求![]() 的分布列與數(shù)學(xué)期望;(數(shù)學(xué)期望值保留到個(gè)位數(shù)字)
的分布列與數(shù)學(xué)期望;(數(shù)學(xué)期望值保留到個(gè)位數(shù)字)
(2)某二手車銷售商專門銷售這一品牌的二手車,且將下一年的交強(qiáng)險(xiǎn)保費(fèi)高于基本保費(fèi)的車輛記為事故車,假設(shè)購(gòu)進(jìn)一輛事故車虧損5000元,一輛非事故車盈利10000元:
①若該銷售商購(gòu)進(jìn)三輛(車齡已滿三年)該品牌二手車,求這三輛車中至多有一輛事故車的概率;
②若該銷售商一次購(gòu)進(jìn)100輛(車齡已滿三年)該品牌二手車,求他獲得利潤(rùn)的期望值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知橢圓C:![]() ,(a>b>0)過(guò)點(diǎn)(1,
,(a>b>0)過(guò)點(diǎn)(1,![]() )且離心率為
)且離心率為![]() .
.
(1)求橢圓C的方程;
(2)設(shè)橢圓C的右頂點(diǎn)為P,過(guò)定點(diǎn)(2,﹣1)的直線l:y=kx+m與橢圓C相交于異于點(diǎn)P的A,B兩點(diǎn),若直線PA,PB的斜率分別為k1,k2,求k1+k2的值.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com