Question

7．如圖，已知雙曲線$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右焦點分別為F₁、F₂，|F₁F₂|=4，P是雙曲線右支上一點，直線PF₂交y軸于點A，△APF₁的內切圓切邊PF₁于點Q，若|PQ|=1，則雙曲線的離心率為2．

Answer 1

分析 由|PQ|=1，△APF₁的內切圓在邊PF₁上的切點為Q，根據切線長定理，可得|PF₁|-|PF₂|=2，結合|F₁F₂|=4，即可得出結論．

解答 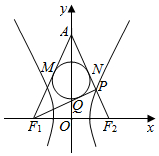解：∵雙曲線的焦距為4，
∴|F₁F₂|=4，∴c=2
∵|PQ|=1，△APF₁的內切圓在邊PF₁上的切點為Q，
∴根據切線長定理可得AM=AN，F₁M=F₁Q，PN=PQ，
∵|AF₁|=|AF₂|，
∴AM+F₁M=AN+PN+NF₂，
∴F₁M=PN+NF₂=PQ+PF₂
∴|PF₁|-|PF₂|=F₁Q+PQ-PF₂=F₁M+PQ-PF₂=PQ+PF₂+PQ-PF₂=2PQ=2，
即2a=2，則a=1，
∵a=1，c=2
∴雙曲線的離心率是e=$\frac{c}{a}$=2．
故答案為：2

點評 本題主要考查雙曲線的離心率，考查三角形內切圓的性質，考查切線長定理，考查學生的計算能力，利用雙曲線的定義進行轉化是解決本題的關鍵．