
【題目】如圖①,已知拋物線y=ax2﹣4amx+3am2(a、m為參數(shù),且a>0,m>0)與x軸交于A、B兩點(A在B的左邊),與y軸交于點C.
(1)求點B的坐標(結(jié)果可以含參數(shù)m);
(2)連接CA、CB,若C(0,3m),求tan∠ACB的值;
(3)如圖②,在(2)的條件下,拋物線的對稱軸為直線l:x=2,點P是拋物線上的一個動點,F是拋物線的對稱軸l上的一點,在拋物線上是否存在點P,使△POF成為以點P為直角頂點的的等腰直角三角形.若存在,求出所有符合條件的點P的坐標,若不存在,請說明理由.

【答案】(1)B(3m,0);(2)tan∠ACB=![]() ;
;
(3)點P的坐標是:(![]() )或(
)或(![]() )或(
)或(![]() )或(
)或(![]() ).
).
【解析】
(1)令y=0,解方程ax2﹣4amx+3am2=0,即可求出點B的坐標;
(2)過點A作AD⊥BC,垂足為點D,可得△BOC為等腰直角三角形,求出AD,CD,則tan∠ACB的值為![]() ;
;
(3)求出拋物線的解析式,分不同的情況:①當P在對稱軸的左邊,如圖3,過P作MN⊥y軸,交y軸于M,交l于N,證明△OMP≌△PNF,根據(jù)|OM|=|PN|,列方程可得點P的坐標;同理可得其他圖形中點P的坐標,②當P在對稱軸的左邊,過P作MN⊥x軸于N,過F作FM⊥MN于M,同理得△ONP≌△PMF,則可求出點P的坐標.
解:(1)令y=0,則有ax2﹣4amx+3am2=0,
解得:x1=m,x2=3m,
∵m>0,A在B的左邊,
∴B(3m,0);
(2)如圖1,過點A作AD⊥BC,垂足為點D,

由(1)可知B(3m,0),則△BOC為等腰直角三角形,
∵OC=OB=3m,
∴BC=3![]() m,
m,
又∵∠ABC=45°,
∴∠DAB=45°,
∴AD=BD,
∵AB=2m,
∴![]() m,CD=2
m,CD=2![]() m,
m,
∴tan∠ACB=![]() ;
;
(3)∵由題意知x=2為對稱軸,
∴2m=2,
即m=1,
∵在(2)的條件下有(0,3m),
∴3m=3am2,
解得m=![]() ,即a=1,
,即a=1,
∴拋物線的解析式為y=x2﹣4x+3,
①當P在對稱軸的左邊,如圖2,過P作MN⊥y軸,交y軸于M,交l于N,

∵△OPF是等腰直角三角形,且OP=PF,
易得△OMP≌△PNF,
∴OM=PN,
∵P(m,m2﹣4m+3),
則﹣m2+4m﹣3=2﹣m,
解得:m=![]() 或
或![]() ,
,
∴P的坐標為(![]() ,
,![]() )或(
)或(![]() );
);
②當P在對稱軸的右邊,
如圖3,過P作MN⊥x軸于N,過F作FM⊥MN于M,

同理得△ONP≌△PMF,
∴PN=FM,
則﹣m2+4m﹣3=m﹣2,
解得:x=![]() 或
或![]() ;
;
P的坐標為(![]() )或(
)或(![]() );
);
綜上所述,點P的坐標是:(![]() )或(
)或(![]() )或(
)或(![]() )或(
)或(![]() ).
).


 期末寶典單元檢測分類復習卷系列答案
期末寶典單元檢測分類復習卷系列答案科目:初中數(shù)學 來源: 題型:
【題目】如圖,反比例函數(shù)y=![]() (k≠0,x>0)的圖象與矩形OABC的邊AB、BC分別交于點E、F,E(
(k≠0,x>0)的圖象與矩形OABC的邊AB、BC分別交于點E、F,E(![]() ,6),且E為BC的中點,D為x軸負半軸上的點.
,6),且E為BC的中點,D為x軸負半軸上的點.

(1)求反比倒函數(shù)的表達式和點F的坐標;
(2)若D(﹣![]() ,0),連接DE、DF、EF,則△DEF的面積是 .
,0),連接DE、DF、EF,則△DEF的面積是 .
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
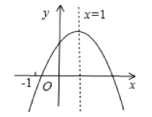
【題目】已知二次函數(shù)y=ax![]() +bx+c的圖象如圖所示,下列結(jié)論:①abc>0;②b<a+c;③4a+2b+c>0;④a+b+c>m(am+b)+c(m≠1的實數(shù)),其中正確的結(jié)論有 ( )
+bx+c的圖象如圖所示,下列結(jié)論:①abc>0;②b<a+c;③4a+2b+c>0;④a+b+c>m(am+b)+c(m≠1的實數(shù)),其中正確的結(jié)論有 ( )
A.![]() 個B.
個B.![]() 個C.
個C.![]() 個D.
個D.![]() 個
個
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
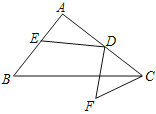
【題目】如圖,在Rt△ABC中,∠A=90°,AB=6,AC=8,D為AC中點,E為AB上的動點,將ED繞點D逆時針旋轉(zhuǎn)90°得到FD,連CF,則線段CF的最小值為_____.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
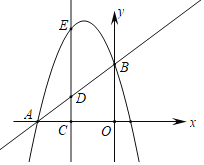
【題目】如圖,已知直線y=x+4交x軸于點A,交y軸于點B,拋物線y=﹣x2+bx+c經(jīng)過點A、B.
(1)求拋物線解析式;
(2)點C(m,0)是x軸上異于A、O點的一點,過點C作x軸的垂線交AB于點D,交拋物線于點E.
①當點E在直線AB上方的拋物線上時,連接AE、BE,求S△ABE的最大值;
②當DE=AD時,求m的值.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
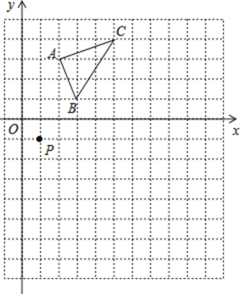
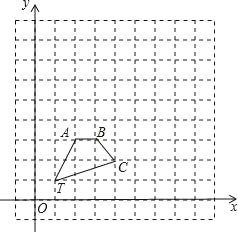
【題目】如圖,在平面直角坐標系中,![]() 的三個頂點坐標分別為
的三個頂點坐標分別為![]() .
.
(1)畫出![]() 關(guān)于
關(guān)于![]() 軸對稱的
軸對稱的![]() ;
;
(2)以點![]() 為位似中心,在如圖所示的網(wǎng)格中畫出
為位似中心,在如圖所示的網(wǎng)格中畫出![]() 的位似圖形
的位似圖形![]() ,使
,使![]() 與
與 ![]() 的相似比為
的相似比為![]() ;
;
(3)點![]() 的坐標是 .
的坐標是 .
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在正方形網(wǎng)格中,四邊形TABC的頂點坐標分別為T(1,1),A(2,3),B(3,3),C(4,2).
(1)以點T(1,1)為位似中心,在位似中心的同側(cè)將四邊形TABC放大為原來的2倍,放大后點A,B,C的對應點分別為A′,B′,C′畫出四邊形TA′B′C′;
(2)寫出點A′,B′,C′的坐標:
A′ ,B′ ,C′ ;
(3)在(1)中,若D(a,b)為線段AC上任一點,則變化后點D的對應點D′的坐標為 .
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】在一個不透明的口袋里裝有若干個除顏色外其余均相同的紅、黃、藍三種顏色的小球,其中紅球2個,籃球1個,若從中任意摸出一個球,摸到球是紅球的概率為![]() .
.
(1)求袋中黃球的個數(shù);
(2)第一次任意摸出一個球(不放回),第二次再摸出一個球,求兩次摸到球的顏色是紅色與黃色這種組合(不考慮紅、黃球順序)的概率.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】先閱讀下列材料,然后解答問題.
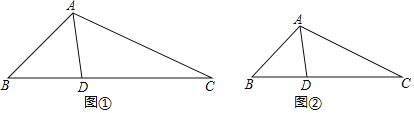
材料:從三角形(不是等腰三角形)一個頂點引出一條射線與對邊相交,頂點與交點之間的線段把這個三角形分割成兩個小三角形,如果分得的兩個小三角形中一個為等腰三角形,另一個與原三角形相似,我們把這條線段叫做這個三角形的完美分割線例如:如圖①,AD把△ABC分成△ABD與△ADC,若△ABD是等腰三角形,且△ADC∽△BAC,那么AD就是△ABC的完美分割線.
解答下列問題:
(1)如圖②,在△ABC中,∠B=40°,AD是△ABC的完美分割線,且△ABD是以AD為底邊的等腰三角形,則∠CAD= 度.
(2)在△ABC中,∠B=42°,AD是△ABC的完美分割線,且△ABD是等腰三角形,求∠BAC的度數(shù).
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com