
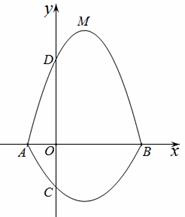
如圖,在平面直角坐標(biāo)系xOy中,A、B為x軸上兩點(diǎn),C、D為y軸上兩點(diǎn),經(jīng)過A、C、B的拋物線的一部分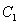 與經(jīng)過點(diǎn)A、D、B的拋物線的一部分
與經(jīng)過點(diǎn)A、D、B的拋物線的一部分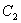 組合成一條封閉曲線,我們把這條封閉曲線稱為“蛋線”.已知點(diǎn)C的坐標(biāo)為(0,
組合成一條封閉曲線,我們把這條封閉曲線稱為“蛋線”.已知點(diǎn)C的坐標(biāo)為(0,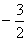 ),點(diǎn)M是拋物線
),點(diǎn)M是拋物線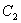 :
: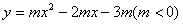 的頂點(diǎn).
的頂點(diǎn).
(1)求A、B兩點(diǎn)的坐標(biāo).
(2)“蛋線 ”在第四象限上是否存在一點(diǎn)P,使得
”在第四象限上是否存在一點(diǎn)P,使得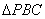 的面積最大?若存在,求出
的面積最大?若存在,求出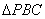 面積的最大值;若不存在,請說明理由;
面積的最大值;若不存在,請說明理由;
(3)當(dāng)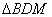 為直角三角形時,直接寫出m的值.______
為直角三角形時,直接寫出m的值.______
解:(1)在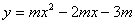 中,
中,
令y=0,則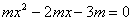 ,解得x=3或x= -1.
,解得x=3或x= -1.
∴A、B兩點(diǎn)的坐標(biāo)為:A(-1,0)、B(3,0).
(2)設(shè)過A、B、C三點(diǎn)的拋物線解析式為 ,
,
 把A(-1,0)、B(3,0)、C(0,
把A(-1,0)、B(3,0)、C(0,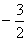 )代入
)代入 中,得
中,得
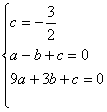 解得
解得 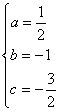
∴ 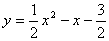 .
.
設(shè)過B(3,0)、C(0,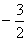 )兩點(diǎn)的解析式為
)兩點(diǎn)的解析式為
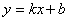 ,
,
代入,得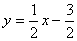 .
.
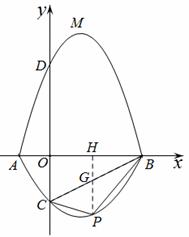
設(shè)“蛋線”在第四象限上存在一點(diǎn)P,過P點(diǎn)作PH⊥AB,垂足為H,交BC于點(diǎn)G.
設(shè)H點(diǎn)坐標(biāo)為(x,0),則G(x,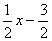 ),P(x,
),P(x,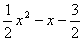 ).
).
則PG=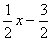 -(
-(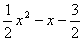 )=
)=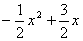 .-
.-
∵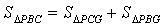
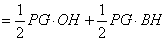
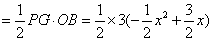
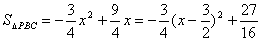
∴“蛋線”在第四象
(3) 或
或



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
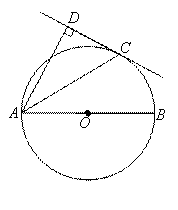
如圖,AB是⊙O的直徑,C是⊙O上一點(diǎn),AD垂直于過點(diǎn)C的直線,
垂足為D,且AC平分∠BAD.
(1) 求證:CD是⊙O的切線;
(2) 若AC=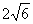 ,AD=4,求AB的長.
,AD=4,求AB的長.
 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
若⊙ O的半徑為5cm,點(diǎn)A到圓心O的距離為4cm,那么點(diǎn)A與⊙ O的位置關(guān) 系是( )
)
A.點(diǎn)A在圓外 B. 點(diǎn)A在圓上 C. 點(diǎn)A在 圓內(nèi) D.不能確定
圓內(nèi) D.不能確定
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
如圖,在標(biāo)有刻度的直線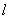 上,從點(diǎn)A開始,
上,從點(diǎn)A開始,
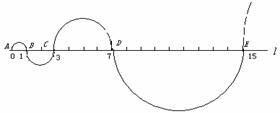 以AB=1為直徑畫半圓,記為第1個半圓;
以AB=1為直徑畫半圓,記為第1個半圓;
以BC=2為直徑畫半圓,記為第2個半圓;
以CD=4為直徑畫半圓,記為第3個半圓;
以DE=8為直徑畫半圓,記為第4個半圓.
……,按此規(guī)律,連續(xù)畫半圓,則第4個
半圓的面積是第3個半圓面積的 倍。第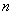 個半圓的面積為 .(結(jié)果保留
個半圓的面積為 .(結(jié)果保留 )
)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
若函數(shù) 的圖象在其所在的每一象限內(nèi),函數(shù)值y隨自變量x的增大而增大,則m的取值范圍是
的圖象在其所在的每一象限內(nèi),函數(shù)值y隨自變量x的增大而增大,則m的取值范圍是
| A.m>1 | B. m>0 | C. m<1 | D.m<0 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
如圖,在平面直角坐標(biāo)系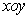 中,⊙A與y軸相切于點(diǎn)
中,⊙A與y軸相切于點(diǎn) ,與x軸相交于M、N兩點(diǎn).如果點(diǎn)M的坐標(biāo)為
,與x軸相交于M、N兩點(diǎn).如果點(diǎn)M的坐標(biāo)為 ,求點(diǎn)N的坐標(biāo).
,求點(diǎn)N的坐標(biāo).

查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com