
【題目】如圖,在平面直角坐標(biāo)系中,點(diǎn)O為坐標(biāo)原點(diǎn),拋物線y=ax2﹣10ax+16a(a≠0)交x軸于A、B兩點(diǎn),拋物線的頂點(diǎn)為D,對稱軸與x軸交于點(diǎn)H,且AB=2DH.
(1)求a的值;
(2)點(diǎn)P是對稱軸右側(cè)拋物線上的點(diǎn),連接PD,PQ⊥x軸于點(diǎn)Q,點(diǎn)N是線段PQ上的點(diǎn),過點(diǎn)N作NF⊥DH于點(diǎn)F,NE⊥PD交直線DH于點(diǎn)E,求線段EF的長;
(3)在(2)的條件下,連接DN、DQ、PB,當(dāng)DN=2QN(NQ>3),2∠NDQ+∠DNQ=90°時,作NC⊥PB交對稱軸左側(cè)的拋物線于點(diǎn)C,求點(diǎn)C的坐標(biāo).
【答案】
(1)
解:令y=0,
∵a≠0,
∴x2﹣10x+16=0,得x=2或x=8,
∴點(diǎn)A(2,0),B(8,0),
∴AB=8﹣2=6,
∵AB=2DH,
∴DH=3,
∵OH=2+ ![]() ,
,
∴D(5,﹣3),
∴﹣3=a×52﹣10a×5+16a,得a= ![]()
(2)
解:如圖1,過點(diǎn)D作PQ的垂線,交PQ的延長線于點(diǎn)M,
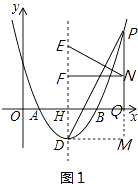
∵NE⊥PD,
∴∠DPN+∠PNE=90°,
∵NF⊥DE,
∴∠FEN+∠FNE=90°,
又∵DH⊥x軸,PQ⊥x軸,
∴DE∥PQ,
∴∠FEN=∠PNE,
∴∠DPM=∠ENF,
∴△EFN∽△DMP,
∴ ![]() ,
,
設(shè)點(diǎn)P(t, ![]() ),
),
則FN=DM=t﹣5,PM= ![]() +3,
+3,
∴ ![]() ,
,
解得,EF=3
(3)
解:如圖2,作QG⊥DN于點(diǎn)G,
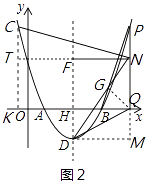
∵DF∥PQ,
∴∠FDN=∠DNQ,
∵2∠NDQ+∠DNQ=90°,
∴2∠NDQ+∠FDN=90°,
∵∠FDM=90°,
∴∠NDM=2∠NDQ,
∴∠NDQ=∠MDQ,
∴QG=QM=DH=3,
設(shè)QN=m,則DN=2m,
∵sin∠DNM= ![]() ,sin∠QNG=
,sin∠QNG= ![]() ,sin∠DNM=sin∠QNG,
,sin∠DNM=sin∠QNG,
∴ ![]() ,得DM=6=DG,
,得DM=6=DG,
∴OQ=5+6=11,
∴點(diǎn)P的縱坐標(biāo)是: ![]() ,
,
∴點(diǎn)P(11,9),
∵NG=DN﹣DG=2m﹣6,在Rt△NGQ中,QG2+NG2=QN2,
∴32+(2m﹣6)2=m2,
解得,m=3(舍去)或m=5,
設(shè)點(diǎn)C的坐標(biāo)為(n, ![]() ),作CK⊥x軸于點(diǎn)K,作NF⊥CK于點(diǎn)K,
),作CK⊥x軸于點(diǎn)K,作NF⊥CK于點(diǎn)K,
則CT= ![]() ,NT=11﹣n,
,NT=11﹣n,
∵P(11,9),則BQ=11﹣8=3,PQ=9,
∵CN⊥PB,PQ∥CK,PQ⊥x軸,
∴△CTN∽△BQP,
∴ ![]() ,
,
即 ![]() ,
,
解得,n=﹣1或n=10(舍去),
∴點(diǎn)C(﹣1,9).
【解析】(1)根據(jù)y=ax2﹣10ax+16a可以求得當(dāng)y=0時,x的值,從而可以求得點(diǎn)A、B的坐標(biāo),由拋物線的頂點(diǎn)為D,對稱軸與x軸交于點(diǎn)H,且AB=2DH,從而可以求得a的值;(2)根據(jù)已知條件作出相應(yīng)的圖形,然后根據(jù)題意題目中的數(shù)量關(guān)系,通過靈活變形可以求得EF的長;(3)根據(jù)題意可以畫出相應(yīng)的圖形,然后根據(jù)題目中的關(guān)系,利用三角形相似,靈活變化可以求得點(diǎn)C的坐標(biāo).
【考點(diǎn)精析】利用二次函數(shù)的圖象和二次函數(shù)的性質(zhì)對題目進(jìn)行判斷即可得到答案,需要熟知二次函數(shù)圖像關(guān)鍵點(diǎn):1、開口方向2、對稱軸 3、頂點(diǎn) 4、與x軸交點(diǎn) 5、與y軸交點(diǎn);增減性:當(dāng)a>0時,對稱軸左邊,y隨x增大而減小;對稱軸右邊,y隨x增大而增大;當(dāng)a<0時,對稱軸左邊,y隨x增大而增大;對稱軸右邊,y隨x增大而減小.


 挑戰(zhàn)100單元檢測試卷系列答案
挑戰(zhàn)100單元檢測試卷系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在方格紙中,A,B,C三點(diǎn)都在小方格的頂點(diǎn)上(每個小方格的邊長為1). 
(1)在圖甲中畫一個以A,B,C為其中三個頂點(diǎn)的平行四邊形,并求出它的周長. 
(2)在圖乙中畫一個經(jīng)過A,B,C三點(diǎn)的圓,并求出圓的面積. 
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系xOy中,已知點(diǎn)A(﹣1,0),B(﹣1,1),C(1,0),D(1,2),點(diǎn)P是坐標(biāo)系內(nèi)一點(diǎn),給出定義:若存在過點(diǎn)P的直線l與線段AB,CD都有公共點(diǎn),則稱點(diǎn)P是線段AB,CD的“聯(lián)絡(luò)點(diǎn)”.現(xiàn)有點(diǎn)P(x,y)在直線y= ![]() x上,且它是線段AB,CD的“聯(lián)絡(luò)點(diǎn)”,則x的取值范圍是 .
x上,且它是線段AB,CD的“聯(lián)絡(luò)點(diǎn)”,則x的取值范圍是 . 
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】李老師為了了解所教班級學(xué)生完成數(shù)學(xué)課前預(yù)習(xí)的具體情況,對本班部分學(xué)生進(jìn)行了為期半個月的跟蹤調(diào)查,他將調(diào)查結(jié)果分為四類,A:很好;B:較好;C:一般;D:較差.并將調(diào)查結(jié)果繪制成以下兩幅不完整的統(tǒng)計圖,請你根據(jù)統(tǒng)計圖解答下列問題: 
(1)李老師一共調(diào)查了多少名同學(xué)?
(2)C類女生有3名,D類男生有1名,將圖1條形統(tǒng)計圖補(bǔ)充完整;
(3)為了共同進(jìn)步,李老師想從被調(diào)查的A類和D類學(xué)生中各隨機(jī)選取一位同學(xué)進(jìn)行“一幫一”互助學(xué)習(xí),請用列表法或畫樹形圖的方法求出所選兩位同學(xué)恰好是一位男同學(xué)和一位女同學(xué)的概率.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,A為某旅游景區(qū)的最佳觀景點(diǎn),游客可從B處乘坐纜車先到達(dá)小觀景平臺DE觀景,然后再由E處繼續(xù)乘坐纜車到達(dá)A處,返程時從A處乘坐升降電梯直接到達(dá)C處,已知:AC⊥BC于C,DE∥BC,AC=200.4米,BD=100米,∠α=30°,∠β=70°,則AE的長度約為米.(參考數(shù)據(jù):sin70≈0.94,cos70°≈0.34,tan70°≈2.25). 
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】為了了解一路段車輛行駛速度的情況,交警統(tǒng)計了該路段上午7::0至9:00來往車輛的車速(單位:千米/時),并繪制成如圖所示的條形統(tǒng)計圖.這些車速的眾數(shù)、中位數(shù)分別是( ) 
A.眾數(shù)是80千米/時,中位數(shù)是60千米/時
B.眾數(shù)是70千米/時,中位數(shù)是70千米/時
C.眾數(shù)是60千米/時,中位數(shù)是60千米/時
D.眾數(shù)是70千米/時,中位數(shù)是60千米/時
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】小明到服裝店進(jìn)行社會實(shí)踐活動,服裝店經(jīng)理讓小明幫助解決以下問題:服裝店準(zhǔn)備購進(jìn)甲乙兩種服裝,甲種每件進(jìn)價80元,售價120元,乙種每件進(jìn)價60元,售價90元.計劃購進(jìn)兩種服裝共100件,其中甲種服裝不少于65件.
(1)若購進(jìn)這100件服裝的費(fèi)用不得超過7500元,則甲種服裝最多購進(jìn)多少件??
(2)在(1)的條件下,該服裝店對甲種服裝以每件優(yōu)惠a(0<a<20)元的價格進(jìn)行促銷活動,乙種服裝價格不變,那么該服裝店應(yīng)如何調(diào)整進(jìn)貨方案才能獲得最大利潤?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,矩形ABCD的對角線AC、BD相交于點(diǎn)0,過點(diǎn)O作OE⊥AC交AB于E,若BC=4,△AOE的面積為6,則cos∠BOE= . 
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com