
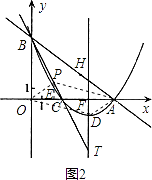
【題目】已知:如圖,在平面直角坐標系xOy中,直線y= ![]() x+6與x軸、y軸的交點分別為A、B兩點,將∠OBA對折,使點O的對應點H落在直線AB上,折痕交x軸于點C.
x+6與x軸、y軸的交點分別為A、B兩點,將∠OBA對折,使點O的對應點H落在直線AB上,折痕交x軸于點C.
(1)直接寫出點C的坐標,并求過A、B、C三點的拋物線的解析式;
(2)若(1)中拋物線的頂點為D,在直線BC上是否存在點P,使得四邊形ODAP為平行四邊形?若存在,求出點P的坐標;若不存在,說明理由;
(3)若把(1)中的拋物線向左平移3.5個單位,則圖象與x軸交于F、N(點F在點N的左側)兩點,交y軸于E點,則在此拋物線的對稱軸上是否存在一點Q,使點Q到E、N兩點的距離之差最大?若存在,請求出點Q的坐標;若不存在,請說明理由.
【答案】
(1)
解:連接CH,
由軸對稱得CH⊥AB,BH=BO,CH=CO
∴在△CHA中由勾股定理,得
AC2=CH2+AH2
∵直線y= ![]() x+6與x軸、y軸的交點分別為A、B兩點,
x+6與x軸、y軸的交點分別為A、B兩點,
∴當x=0時,y=6,當y=0時,x=8
∴B(0,6),A(8,0)
∴OB=6,OA=8,
在Rt△AOB中,由勾股定理,得
AB=10
設C(a,0),∴OC=a
∴CH=a,AH=4,AC=8﹣a,在Rt△AHC中,
由勾股定理,得
(8﹣a)2=a2+42解得
a=3
C(3,0)
設拋物線的解析式為:y=ax2+bx+c,由題意,得
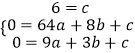
解得: 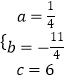
∴拋物線的解析式為:y= ![]() x2
x2 ![]() +6,
+6,
∴y= ![]()
![]()
![]()

(2)
解:由(1)的結論,得
D( ![]() ,﹣
,﹣ ![]() )
)
∴DF= ![]() ,
,
設BC的解析式為:y=kx+b,則有
![]()
解得: ![]()
直線BC的解析式為:y=﹣2x+6
設存在點P使四邊形ODAP是平行四邊形,P(m,n)
作PE⊥OA于E,HD交OA于F.
∴∠PEO=∠AFD=90°,PO=DA,PO∥DA
∴∠POE=∠DAF
∴△OPE≌△ADF
∴PE=DF=n= ![]() ,
,
∴ ![]() =﹣2x+6
=﹣2x+6
∴ ![]()
P( ![]() ,
, ![]() )
)
當x= ![]() 時,
時,
y=﹣2× ![]() +6=1≠
+6=1≠ ![]()
∴點P不再直線BC上,即直線BC上不存在滿足條件的點P
(3)
解:由題意得,平移后的解析式為:
y= ![]() (x﹣2)2
(x﹣2)2 ![]()
∴對稱軸為:x=2,
當x=0時,y=﹣ ![]()
當y=0時,0= ![]() (x﹣2)2
(x﹣2)2 ![]()
解得:x1= ![]() ;x2=
;x2= ![]()
∵F在N的左邊
F( ![]() ,0),E(0,﹣
,0),E(0,﹣ ![]() ),N(
),N( ![]() ,0)
,0)
連接EF交x=2于Q,設EF的解析式為:y=kx+b,則有

解得: 
∴EF的解析式為:y=﹣ ![]() x﹣
x﹣ ![]()
∴ 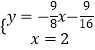
解得:
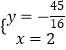
∴Q(2,﹣ ![]() ).
).
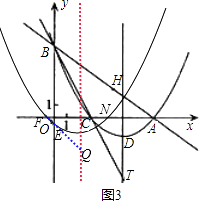
【解析】(1)根據軸對稱和角平分線的性質以及勾股定理可以求出OC的長度,從而求出點C的坐標.再根據直線的解析式求出A、B的坐標,最后利用待定系數法就可以求出拋物線的解析式.(2)根據(1)的解析式可以轉化為頂點式而求出頂點坐標D,利用B、C的坐標求出BC的解析式,假設在直線BC上存在滿足條件的點P,利用平行四邊形的性質和三角形全等的性質求出點P的坐標,得到點P不在直線BC上,而得出結論.(3)平移后根據(1)的解析式可以得到平移后的解析式,頂點坐標及對稱軸,可以求出與坐標軸的交點F、N、E的坐標,連接EF,根據E、F的坐標求出其解析式,求出EF與對稱軸的交點,就是Q點.
【考點精析】本題主要考查了二次函數的圖象和二次函數的性質的相關知識點,需要掌握二次函數圖像關鍵點:1、開口方向2、對稱軸 3、頂點 4、與x軸交點 5、與y軸交點;增減性:當a>0時,對稱軸左邊,y隨x增大而減小;對稱軸右邊,y隨x增大而增大;當a<0時,對稱軸左邊,y隨x增大而增大;對稱軸右邊,y隨x增大而減小才能正確解答此題.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,一艘海輪位于燈塔P的北偏東64°方向,距離燈塔120海里的A處,它沿正南方向航行一段時間后,到達位于燈塔P的南偏東45°方向上的B處,求BP和BA的長(結果取整數).
參考數據:sin64°≈0.90,cos64°≈0.44,tan64°≈2.05, ![]() 取1.414.
取1.414.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在Rt△ABC中,∠ACB=90°,點D是邊AB的中點,點E在邊BC上,AE=BE,點M是AE的中點,聯結CM,點G在線段CM上,作∠GDN=∠AEB交邊BC于N. 
(1)如圖2,當點G和點M重合時,求證:四邊形DMEN是菱形;
(2)如圖1,當點G和點M、C不重合時,求證:DG=DN.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在直角坐標系中,⊙M經過原點O(0,0),點A( ![]() ,0)與點B(0,﹣
,0)與點B(0,﹣ ![]() ),點D在劣弧
),點D在劣弧 ![]() 上,連接BD交x軸于點C,且∠COD=∠CBO.
上,連接BD交x軸于點C,且∠COD=∠CBO. 
(1)求⊙M的半徑;
(2)求證:BD平分∠ABO;
(3)在線段BD的延長線上找一點E,使得直線AE恰好為⊙M的切線,求此時點E的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,等腰直角三角形OAB的一條直角邊在y軸上,點P是邊AB上的一個動點,過點P的反比例函數y= ![]() 的圖象交斜邊OB于點Q,
的圖象交斜邊OB于點Q,
(1)當Q為OB中點時,AP:PB=
(2)若P為AB的三等分點,當△AOQ的面積為 ![]() 時,k的值為
時,k的值為 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知點A(﹣2,1),B(1,4),若反比例函數y= ![]() 與線段AB有公共點時,k的取值范圍是( )
與線段AB有公共點時,k的取值范圍是( )
A.﹣2≤k≤4
B.k≤﹣2或k≥4
C.﹣2≤k<0或k≥4
D.﹣2≤k<0或0<k≤4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在正方形ABCD中,對角線AC、BD交于點O,動點P在線段BC上(不含點B),∠BPE= ![]() ∠ACB,PE交BO于點E,過點B作BF⊥PE,垂足為F,交AC于點G.
∠ACB,PE交BO于點E,過點B作BF⊥PE,垂足為F,交AC于點G.
(1)當點P與點C重合時(如圖①),求證:△BOG≌△POE;
(2)通過觀察、測量、猜想: ![]() =
= ![]() ,并結合圖②證明你的猜想;
,并結合圖②證明你的猜想;
(3)把正方形ABCD改為菱形,其他條件不變(如圖③),若∠ACB=α,求 ![]() 的值.(用含α的式子表示)
的值.(用含α的式子表示)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形OABC中,OA=3,OC=2,F是AB上的一個動點(F不與A,B重合),過點F的反比例函數![]() (k>0)的圖象與BC邊交于點E.
(k>0)的圖象與BC邊交于點E.
(1)當F為AB的中點時,求該函數的解析式;
(2)當k為何值時,△EFA的面積最大,最大面積是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com