
【題目】在等腰直角△ABC中,∠ACB=90°,P是線段BC上一動點(與點B、C不重合),連接AP,延長BC至點Q,使得CQ=CP,過點Q作QH⊥AP于點H,交AB于點M. 
(1)若∠PAC=α,求∠AMQ的大小(用含α的式子表示).
(2)用等式表示線段MB與PQ之間的數量關系,并證明.
【答案】
(1)解:∠AMQ=45°+α;理由如下:
∵∠PAC=α,△ACB是等腰直角三角形,
∴∠BAC=∠B=45°,∠PAB=45°﹣α,
∵QH⊥AP,
∴∠AHM=90°,
∴∠AMQ=180°﹣∠AHM﹣∠PAB=45°+α
(2)解:PQ= ![]() MB;理由如下:
MB;理由如下:
連接AQ,作ME⊥QB,如圖所示:
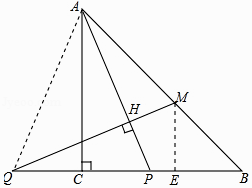
∵AC⊥QP,CQ=CP,
∴∠QAC=∠PAC=α,
∴∠QAM=45°+α=∠AMQ,
∴AP=AQ=QM,
在△APC和△QME中, 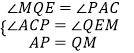 ,
,
∴△APC≌△QME(AAS),
∴PC=ME,
∴△AEB是等腰直角三角形,
∴ ![]() PQ=
PQ= ![]() MB,
MB,
∴PQ= ![]() MB.
MB.
【解析】(1)由等腰直角三角形的性質得出∠BAC=∠B=45°,∠PAB=45°﹣α,由直角三角形的性質即可得出結論;(2)連接AQ,作ME⊥QB,由AAS證明△APC≌△QME,得出PC=ME,△AEB是等腰直角三角形,由等腰直角三角形的性質即可得出結論.
【考點精析】根據題目的已知條件,利用等腰直角三角形的相關知識可以得到問題的答案,需要掌握等腰直角三角形是兩條直角邊相等的直角三角形;等腰直角三角形的兩個底角相等且等于45°.


科目:初中數學 來源: 題型:
【題目】定義:點A(x,y)為平面直角坐標系內的點,若滿足x=y,則把點A 叫做“平衡點”.例如:M(1,1),N(﹣2,-2)都是“平衡點”.當﹣1≤x≤3 時,直線y=2x+m 上有“平衡點”,則m 的取值范圍是( )
A.0≤m≤1
B.﹣1≤m≤0
C.﹣3≤m≤3
D.﹣3≤m≤1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,△ABC位于第二象限,點A的坐標是(﹣2,3),先把△ABC向右平移4個單位長度得到△A1B1C1 , 再作與△A1B1C1關于x軸對稱的△A2B2C2 , 則點A的對應點A2的坐標是( )
A.(﹣3,2)
B.(2,﹣3)
C.(1,﹣2)
D.(﹣1,2)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下面的統計圖反映了我國與“一帶一路”沿線部分地區的貿易情況. 2011﹣2016年我國與東南亞地區和東歐地區的貿易額統計圖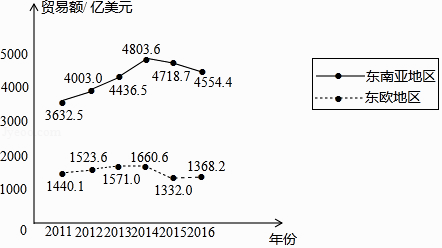
(以上數據摘自《“一帶一路”貿易合作大數據報告(2017)》)
根據統計圖提供的信息,下列推理不合理的是( )
A.與2015年相比,2016年我國與東歐地區的貿易額有所增長
B.2011﹣2016年,我國與東南亞地區的貿易額逐年增長
C.2011﹣2016年,我國與東南亞地區的貿易額的平均值超過4200億美元
D.2016年我國與東南亞地區的貿易額比我國與東歐地區的貿易額的3倍還多
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,函數y= ![]() (x>0)的圖象與直線y=x﹣2交于點A(3,m).
(x>0)的圖象與直線y=x﹣2交于點A(3,m). 
(1)求k、m的值;
(2)已知點P(n,n)(n>0),過點P作平行于x軸的直線,交直線y=x﹣2于點M,過點P作平行于y軸的直線,交函數y= ![]() (x>0)的圖象于點N. ①當n=1時,判斷線段PM與PN的數量關系,并說明理由;
(x>0)的圖象于點N. ①當n=1時,判斷線段PM與PN的數量關系,并說明理由;
②若PN≥PM,結合函數的圖象,直接寫出n的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,多邊形的各頂點都在方格紙的格點(橫豎格子線的交錯點)上,這樣的多邊形稱為格點多邊形,它的面積S可用公式S=a+ ![]() b﹣1(a是多邊形內的格點數,b是多邊形邊界上的格點數)計算,這個公式稱為“皮克定理”.現用一張方格紙共有200個格點,畫有一個格點多邊形,它的面積S=40.
b﹣1(a是多邊形內的格點數,b是多邊形邊界上的格點數)計算,這個公式稱為“皮克定理”.現用一張方格紙共有200個格點,畫有一個格點多邊形,它的面積S=40.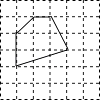
(1)這個格點多邊形邊界上的格點數b=(用含a的代數式表示).
(2)設該格點多邊形外的格點數為c,則c﹣a= .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AC、BD為圓O的兩條互相垂直的直徑,動點P從圓心O出發,沿O→C→D→O的路線作勻速運動,設運動時間為t秒,∠APB的度數為y度,那么表示y與t之間函數關系的圖象大致為( )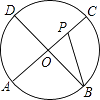
A.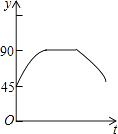
B.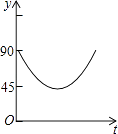
C.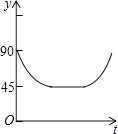
D.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在邊長為4的正方形ABCD中,動點P從A點出發,以每秒1個單位長度的速度沿AB向B點運動,同時動點Q從B點出發,以每秒2個單位長度的速度沿BC→CD方向運動,當P運動到B點時,P、Q兩點同時停止運動.設P點運動的時間為t,△APQ的面積為S,則S與t的函數關系的圖象是( )
A.
B.
C.
D.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com