
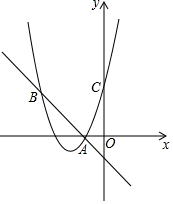
 如圖,已知二次函數y1=ax2+bx+c的圖象經過點A(-1,0),C(0,3),且對稱軸為直線x=-2,一次函數y2=mx+n的圖象經過點A、B.
如圖,已知二次函數y1=ax2+bx+c的圖象經過點A(-1,0),C(0,3),且對稱軸為直線x=-2,一次函數y2=mx+n的圖象經過點A、B.分析 (1)利用待定系數法,把問題轉化為方程組解決即可.
(2)根據函數圖象,二次函數圖象在一次函數圖象的上方,注意等于號.
解答 解:(1)由題意$\left\{\begin{array}{l}{a-b+c=0}\\{c=3}\\{-\frac{b}{2a}=-2}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=1}\\{b=4}\\{c=3}\end{array}\right.$,
∴二次函數的解析式為y=x2+4x+3.
(2)觀察推出可知,y1-y2≥0時,x≤-4或x≥-1.
點評 本題考查二次函數的應用、一次函數的應用、待定系數法等知識,解題的關鍵是熟練掌握待定系數法確定函數解析式,學會利用圖象根據條件確定自變量的取值范圍.


 每日10分鐘口算心算速算天天練系列答案
每日10分鐘口算心算速算天天練系列答案科目:初中數學 來源: 題型:解答題
 已知:如圖,在△ABC中,∠C=90°,AC=BC=$\sqrt{2}$,將△ABC繞點A順時針方向旋轉60°到△AB′C′的位置,連結BC′,求BC′的長.
已知:如圖,在△ABC中,∠C=90°,AC=BC=$\sqrt{2}$,將△ABC繞點A順時針方向旋轉60°到△AB′C′的位置,連結BC′,求BC′的長.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 第一套 | 第二套 | |
| x(cm) | 40 | 37 |
| y(cm) | 75 | 70.2 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
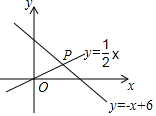 (1)計算(2$\sqrt{3}$-1)2
(1)計算(2$\sqrt{3}$-1)2查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,某大學計劃在一塊長80m,寬60m的長方形場地中央建一個長方形網球場,四周留出寬度相等的人行走道(陰影部分).設人行走道的寬為x(m),求網球場的面積.
如圖,某大學計劃在一塊長80m,寬60m的長方形場地中央建一個長方形網球場,四周留出寬度相等的人行走道(陰影部分).設人行走道的寬為x(m),求網球場的面積.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,在平面直角坐標系中,一次函數y=kx+b(k≠0)的圖象與反比例函數y=$\frac{m}{x}$(m≠0)的圖象交于A、B兩點,與x軸交于C點,與y軸交于D點;點A的坐標為(n,6),點C的坐標為(-2,0),且tan∠ACO=2.
如圖,在平面直角坐標系中,一次函數y=kx+b(k≠0)的圖象與反比例函數y=$\frac{m}{x}$(m≠0)的圖象交于A、B兩點,與x軸交于C點,與y軸交于D點;點A的坐標為(n,6),點C的坐標為(-2,0),且tan∠ACO=2.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
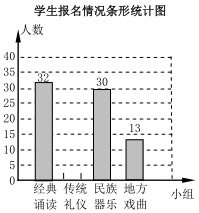 為推進“傳統文化進校園”活動,某校準備成立“經典誦讀”、“傳統禮儀”、“民族器樂”和“地方戲 曲”等四個課外活動小組.學生報名情況如圖(每人只能選擇一個小組):
為推進“傳統文化進校園”活動,某校準備成立“經典誦讀”、“傳統禮儀”、“民族器樂”和“地方戲 曲”等四個課外活動小組.學生報名情況如圖(每人只能選擇一個小組):查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com