
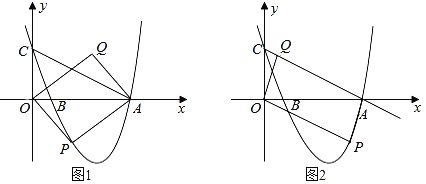
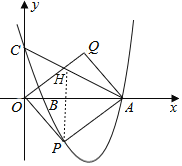
【題目】如圖1所示,拋物線![]() 與x軸交于A、B兩點(diǎn),與y軸交于點(diǎn)C,已知C點(diǎn)坐標(biāo)為(0,4),拋物線的頂點(diǎn)的橫坐標(biāo)為
與x軸交于A、B兩點(diǎn),與y軸交于點(diǎn)C,已知C點(diǎn)坐標(biāo)為(0,4),拋物線的頂點(diǎn)的橫坐標(biāo)為![]() ,點(diǎn)P是第四象限內(nèi)拋物線上的動(dòng)點(diǎn),四邊形OPAQ是平行四邊形,設(shè)點(diǎn)P的橫坐標(biāo)為m.
,點(diǎn)P是第四象限內(nèi)拋物線上的動(dòng)點(diǎn),四邊形OPAQ是平行四邊形,設(shè)點(diǎn)P的橫坐標(biāo)為m.
(1)求拋物線的解析式;
(2)求使△APC的面積為整數(shù)的P點(diǎn)的個(gè)數(shù);
(3)當(dāng)點(diǎn)P在拋物線上運(yùn)動(dòng)時(shí),四邊形OPAQ可能是正方形嗎?若可能,請求出點(diǎn)P的坐標(biāo),若不可能,請說明理由;
(4)在點(diǎn)Q隨點(diǎn)P運(yùn)動(dòng)的過程中,當(dāng)點(diǎn)Q恰好落在直線AC上時(shí),則稱點(diǎn)Q為“和諧點(diǎn)”,如圖(2)所示,請直接寫出當(dāng)Q為“和諧點(diǎn)”的橫坐標(biāo)的值.
【答案】(1)![]() ;(2)9個(gè) ;(3)
;(2)9個(gè) ;(3)![]() 或
或![]() ;(4)
;(4)![]()
【解析】
(1)拋物線與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() ,頂點(diǎn)的橫坐標(biāo)為
,頂點(diǎn)的橫坐標(biāo)為![]() ,則
,則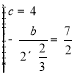 ,即可求解;
,即可求解;
(2)![]() 的面積
的面積![]() ,即可求解;
,即可求解;
(3)當(dāng)四邊形![]() 是正方形時(shí),點(diǎn)
是正方形時(shí),點(diǎn)![]() 只能在
只能在![]() 軸的下方,此時(shí)
軸的下方,此時(shí)![]() 為等腰直角三角形,設(shè)點(diǎn)
為等腰直角三角形,設(shè)點(diǎn)![]() ,則
,則![]() ,即可求解;
,即可求解;
(4)求出直線![]() 的表達(dá)式為:
的表達(dá)式為:![]() ,則直線
,則直線![]() 的表達(dá)式為:
的表達(dá)式為:![]() ②,聯(lián)立①②求出
②,聯(lián)立①②求出![]() 的坐標(biāo),又四邊形
的坐標(biāo),又四邊形![]() 是平行四邊形,則
是平行四邊形,則![]() 的中點(diǎn)即為
的中點(diǎn)即為![]() 的中點(diǎn),即可求解.
的中點(diǎn),即可求解.
解:(1)拋物線與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() ,頂點(diǎn)的橫坐標(biāo)為
,頂點(diǎn)的橫坐標(biāo)為![]() ,則
,則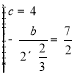 ,解得
,解得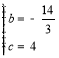 ,
,
故拋物線的拋物線為:![]() ;
;
(2)對于![]() ,令
,令![]() ,則
,則![]() 或6,故點(diǎn)
或6,故點(diǎn)![]() 、
、![]() 的坐標(biāo)分別為
的坐標(biāo)分別為![]() 、
、![]() ;
;
如圖,過點(diǎn)![]() 作
作![]() 軸交
軸交![]() 于點(diǎn)
于點(diǎn)![]() ,
,
設(shè)直線![]() 的表達(dá)式為:
的表達(dá)式為:![]()
由點(diǎn)![]() (6,0)、
(6,0)、![]() (0,4)的坐標(biāo)得
(0,4)的坐標(biāo)得![]() ,解得
,解得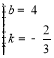 ,
,
∴直線![]() 的表達(dá)式為:
的表達(dá)式為:![]() ①,
①,
設(shè)點(diǎn)![]() ,則點(diǎn)
,則點(diǎn)![]() ,
,
![]() 的面積
的面積![]() ,
,
當(dāng)![]() 時(shí),
時(shí),![]() ,當(dāng)
,當(dāng)![]() 時(shí),
時(shí),![]() ,
,
故使![]() 的面積為整數(shù)的
的面積為整數(shù)的![]() 點(diǎn)的個(gè)數(shù)為9個(gè);
點(diǎn)的個(gè)數(shù)為9個(gè);
(3)當(dāng)四邊形![]() 是正方形時(shí),點(diǎn)
是正方形時(shí),點(diǎn)![]() 只能在
只能在![]() 軸的下方,
軸的下方,
此時(shí)![]() 為等腰直角三角形,設(shè)點(diǎn)
為等腰直角三角形,設(shè)點(diǎn)![]() ,則
,則![]() ,
,
即![]() ,解得:
,解得:![]() 或4,
或4,
故點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,
,![]() 或
或![]() ;
;
(4)設(shè)點(diǎn)![]() ,為點(diǎn)
,為點(diǎn)![]() ,
,
設(shè)直線![]() 的表達(dá)式為:
的表達(dá)式為:![]() ,
,
由點(diǎn)![]() ,
,![]() 的坐標(biāo)可得
的坐標(biāo)可得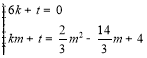 ,解之得:
,解之得: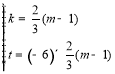
∴直線![]() 的表達(dá)式為:
的表達(dá)式為:![]() ,
,
![]() ,則
,則![]() 和
和![]() 表達(dá)式中的
表達(dá)式中的![]() 值相同,
值相同,
故直線![]() 的表達(dá)式為:
的表達(dá)式為:![]() ②,
②,
聯(lián)立①②得: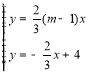 ,解得:
,解得: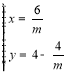 ,
,
則點(diǎn)![]() ,
,![]() ,
,
![]() 四邊形
四邊形![]() 是平行四邊形,則
是平行四邊形,則![]() 的中點(diǎn)即為
的中點(diǎn)即為![]() 的中點(diǎn),
的中點(diǎn),
如圖2,作![]() 軸于點(diǎn)C,
軸于點(diǎn)C,![]() 軸于點(diǎn)D,
軸于點(diǎn)D,
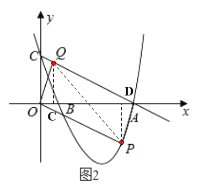
∴![]() ,
,
則有,![]() ,解得:
,解得:![]() ,
,
經(jīng)檢驗(yàn),![]() 是原分式方程得跟,
是原分式方程得跟,
則![]() ,
,
故![]() 的橫坐標(biāo)的值為
的橫坐標(biāo)的值為![]() .
.


 閱讀快車系列答案
閱讀快車系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】為宣傳普及新冠肺炎防治知識,引導(dǎo)學(xué)生做好防控.某校舉行了主題為“防控新冠,從我做起”的線上知識競賽活動(dòng),測試內(nèi)容為20道判斷題,每道題5分,滿分100分,為了解八、九年級學(xué)生此次競賽成績的情況,分別隨機(jī)在八、九年級各抽取了20名參賽學(xué)生的成績.已知抽查得到的八年級的數(shù)據(jù)如下:80,95,75,75,90,75,80,65,80,85,75,65,70,65,85,70,95,80,75,80.
為了便于分析數(shù)據(jù),統(tǒng)計(jì)員對八年級數(shù)據(jù)進(jìn)行了整理,得到了表一:
成績等級 | 分?jǐn)?shù)(單位:分) | 學(xué)生數(shù) |
D等 | 60<x≤70 | 5 |
C等 | 70<x≤80 | a |
B等 | 80<x≤90 | b |
A等 | 90<x≤100 | 2 |
九年級成績的平均數(shù)、中位數(shù)、優(yōu)秀率如下:(分?jǐn)?shù)80分以上、不含80分為優(yōu)秀)
年級 | 平均數(shù) | 中位數(shù) | 優(yōu)秀率 |
八年級 | 77.5 | c | m% |
九年級 | 76 | 82.5 | 50% |
(1)根據(jù)題目信息填空:a= ,c= ,m= ;
(2)八年級小宇和九年級小樂的分?jǐn)?shù)都為80分,請判斷小宇、小樂在各自年級的排名哪位更靠前?請簡述你的理由;
(3)若九年級共有600人參加參賽,請估計(jì)九年級80分以上的人數(shù).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖11,一轉(zhuǎn)盤被等分成三個(gè)扇形,上面分別標(biāo)有關(guān)-1,1,
2中的一個(gè)數(shù),指針位置固定,轉(zhuǎn)動(dòng)轉(zhuǎn)盤后任其自由停止,這時(shí),鞭個(gè)扇形恰好停在指針?biāo)?/span>
指的位置,并相應(yīng)得到這個(gè)扇形上的數(shù)(若指針恰好指在等分線上,當(dāng)做指向右邊的扇形).
⑴若小靜轉(zhuǎn)動(dòng)轉(zhuǎn)盤一次,求得到負(fù)數(shù)的概率;
⑵小宇和小靜分別轉(zhuǎn)動(dòng)一次,若兩人得到的數(shù)相同,則稱兩人“不謀而合”,用列表法(或畫樹形圖)求兩人“不謀而合”的概率.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() 在一條直線上,
在一條直線上,![]() ,連接
,連接![]() ,
,![]() 交于點(diǎn)
交于點(diǎn)![]() ,連接
,連接![]() .下列結(jié)論:①
.下列結(jié)論:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 平分
平分![]() .其中正確的是( )
.其中正確的是( )

A.①②③B.①②④C.②③④D.①②③④
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
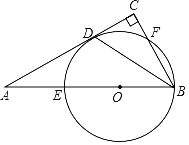
【題目】如圖所示,Rt△ABC中:∠C=90°,AB=6,在AB上取點(diǎn)O,以O為圓心,以OB為半徑作圓,與AC相切于點(diǎn)D,并分別與AB,BC相交于點(diǎn)E,F(異于點(diǎn)B).
(1)求證:BD平分∠ABC;
(2)若點(diǎn)E恰好是AO的中點(diǎn),求弧BF的長;
(3)若CF的長為1,求⊙O的半徑長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系中,二次函數(shù)y=﹣x2+6x﹣5的圖象與x軸交于A、B兩點(diǎn),與y軸交于點(diǎn)C,其頂點(diǎn)為P,連接PA、AC、CP,過點(diǎn)C作y軸的垂線l.
(1)P的坐標(biāo) ,C的坐標(biāo) ;
(2)直線1上是否存在點(diǎn)Q,使△PBQ的面積等于△PAC面積的2倍?若存在,求出點(diǎn)Q的坐標(biāo);若不存在,請說明理由.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
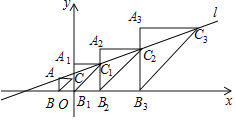
【題目】如圖,在平面直角坐標(biāo)系中,![]() ABC,
ABC,![]() A1B1C1,
A1B1C1,![]() A2B2C2,
A2B2C2,![]() A3B3C3…
A3B3C3…![]() AnBnCn都是等腰直角三角形,點(diǎn)B,B1,B2,B3…Bn都在x軸上,點(diǎn)B1與原點(diǎn)重合,點(diǎn)A,C1,C2,C3…Cn都在直線l:y=
AnBnCn都是等腰直角三角形,點(diǎn)B,B1,B2,B3…Bn都在x軸上,點(diǎn)B1與原點(diǎn)重合,點(diǎn)A,C1,C2,C3…Cn都在直線l:y=![]() x+
x+![]() 上,點(diǎn)C在y軸上,AB∥A1B1∥A2B2∥…∥AnBn∥y軸,AC∥A1C1∥A2C2∥…∥AnCn∥x軸,若點(diǎn)A的橫坐標(biāo)為﹣1,則點(diǎn)Cn的縱坐標(biāo)是_____.
上,點(diǎn)C在y軸上,AB∥A1B1∥A2B2∥…∥AnBn∥y軸,AC∥A1C1∥A2C2∥…∥AnCn∥x軸,若點(diǎn)A的橫坐標(biāo)為﹣1,則點(diǎn)Cn的縱坐標(biāo)是_____.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
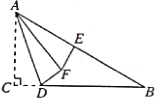
【題目】如圖,已知在△ABC中,![]() ,
,![]() ,
,![]() ,點(diǎn)E為AB的中點(diǎn),D為BC邊上的一動(dòng)點(diǎn),把△ACD沿AD折疊,點(diǎn)C落在點(diǎn)F處,當(dāng)△AEF為直角三角形時(shí),CD的長為__________.
,點(diǎn)E為AB的中點(diǎn),D為BC邊上的一動(dòng)點(diǎn),把△ACD沿AD折疊,點(diǎn)C落在點(diǎn)F處,當(dāng)△AEF為直角三角形時(shí),CD的長為__________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】九年級某班準(zhǔn)備選拔四名男生參加學(xué)校運(yùn)動(dòng)會接力比賽,進(jìn)行了一次50米短跑測驗(yàn),成績?nèi)缦拢?/span>(單位:秒)6.9 7.0 7.1 7.2 7.0 7.4 7.3 7.5 7.0 7.4 7.3 6.8 7.0 7.1 7.3 6.9 7.1 7.2 7.4 6.9 7.0 7.2 7.0 7.2 7.6
班主任老師按0.2秒的組距分段,統(tǒng)計(jì)每個(gè)成績段出現(xiàn)的頻數(shù),填入頻數(shù)分布表,并繪制了頻數(shù)分布直方圖.
成績段(秒) |
|
|
|
|
|
頻數(shù) | 4 | 9 | 7 |
| 1 |
頻率 |
| 0.36 | 0.28 | 0.16 | 0.04 |
(1)求a、b值,并將頻數(shù)分布直方圖補(bǔ)充完整;
(2)請計(jì)算這次短跑測驗(yàn)的優(yōu)秀率(7.0秒及7.0秒以下);
(3)成績前四名的A、B、C、D同學(xué)組成九年級某班4×100米接力隊(duì),其中成績最好的A同學(xué)安排在最后一棒(第4棒),另外三位同學(xué)隨機(jī)編排在其余三個(gè)棒次,畫樹狀圖或列表說明B、C兩位同學(xué)為相鄰棒次的概率.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com