
3.(P14習(xí)題9)一個集合的所有子集共有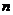 個,若
個,若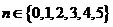 ,則
,則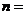 {1,2.4}
{1,2.4}
2.(P13練習(xí)5)設(shè)
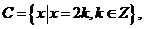 則
則 A,
A,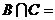
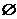 ,
, R,
R, A。
A。
1.設(shè) ,則
,則 (1,2)
(1,2)
步驟:1、假設(shè)結(jié)論反面成立;2、從這個假設(shè)出發(fā),推理論證,得出矛盾;
3、由矛盾判斷假設(shè)不成立,從而肯定結(jié)論正確。
|
正面詞語 |
等于 |
大于 |
小于 |
是 |
都是 |
至多有一個 |
|||
|
否定 |
不等于 |
不大于 |
不小于 |
不是 |
不都是 |
至少有兩個 |
|||
|
|
|||||||||
|
正面詞語 |
至少有一個 |
任意的 |
所有的 |
至多有n個 |
任意兩個 |
||||
|
否定 |
一個也沒有 |
某些 |
存在 |
至少n+1個 |
存在兩個不 |
||||
課本題
注意:“若 ,則
,則 ”在解題中的運(yùn)用,
”在解題中的運(yùn)用,
如:“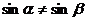 ”是“
”是“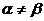 ”的充分不必要條件。
”的充分不必要條件。
若p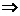 q,q
q,q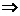 p;則
p;則 是
是 的充分非必要條件
的充分非必要條件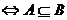 ;
;
若p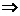 q,q
q,q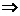 p;則
p;則 是
是 的必要非充分條件
的必要非充分條件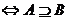 ;
;
若p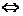 q;則
q;則 是
是 的充要條件
的充要條件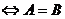 ;
;
若p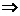 q,q
q,q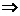 p;則
p;則 是
是 的既非充分又非必要條件
的既非充分又非必要條件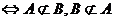 ;
;
(1)若集合 中有
中有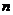 個元素,則集合
個元素,則集合 的所有不同的子集個數(shù)為2
的所有不同的子集個數(shù)為2 ,所有真子集的個數(shù)是2
,所有真子集的個數(shù)是2 -1,所有非空真子集的個數(shù)是2
-1,所有非空真子集的個數(shù)是2 -2。
-2。
(2) 中元素的個數(shù)的計(jì)算公式為:
中元素的個數(shù)的計(jì)算公式為:


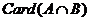 ;
;
(3)韋恩圖的運(yùn)用:
(1)符號“ ”是表示元素與集合之間關(guān)系的,立體幾何中的體現(xiàn) 點(diǎn)與直線(面)的關(guān)系 ;
”是表示元素與集合之間關(guān)系的,立體幾何中的體現(xiàn) 點(diǎn)與直線(面)的關(guān)系 ;
符號“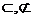 ”是表示集合與集合之間關(guān)系的,立體幾何中的體現(xiàn) 面與直線(面)的關(guān)系 。
”是表示集合與集合之間關(guān)系的,立體幾何中的體現(xiàn) 面與直線(面)的關(guān)系 。
(2)A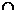 B={
x| x
B={
x| x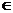 A且x
A且x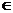 B} A
B} A B={
x| x
B={
x| x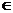 A或x
A或x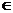 B};
B};
C A={
x| x
A={
x| x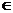 I且x
I且x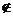 A}
A}
(3)對于任意集合 ,則:
,則:
① ;
;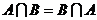 ;
;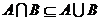 ;
;
②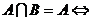 A
A B;
B; B
B A
;
A
;
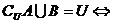 A
A B=
B=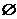 ;
; A
A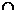 B=U;
B=U;
③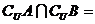
 ;
; 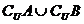
 ;
;
(4)①若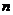 為偶數(shù),則
為偶數(shù),則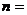 2K,(k
2K,(k );若
);若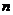 為奇數(shù),則
為奇數(shù),則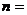 2k+1, (k
2k+1, (k );
);
②若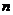 被3除余0,則
被3除余0,則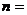 3k, (k
3k, (k );若
);若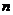 被3除余1,則
被3除余1,則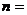 3k+1(k
3k+1(k );若
);若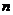 被3除余2,則
被3除余2,則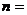 3k+2(k
3k+2(k );
);
(1)集合中元素的特征:確定性,互異性,無序性 。
(2)集合與元素的關(guān)系用符號 表示。
表示。
(3)常用數(shù)集的符號表示:自然數(shù)集 N ;正整數(shù)集 N 、 N
、 N ;整數(shù)集 Z ;有理數(shù)集 Q 、實(shí)數(shù)集 R 。
;整數(shù)集 Z ;有理數(shù)集 Q 、實(shí)數(shù)集 R 。
(4)集合的表示法:列舉法,描述法,符號法(數(shù)軸法,韋恩圖法)
注意:區(qū)分集合中元素的形式:如: ;
;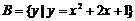 ;
;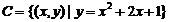
 ;
; ;
;
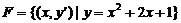 ;
;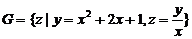
(5)空集是指不含任何元素的集合。(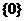 、
、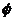 和
和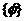 的區(qū)別;0與三者間的關(guān)系)
的區(qū)別;0與三者間的關(guān)系)
空集是任何集合的子集,是任何非空集合的真子集。
注意:條件為 ,在討論的時候不要遺忘了
,在討論的時候不要遺忘了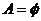 的情況。
的情況。
如: ,如果
,如果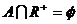 ,求
,求 的取值。
的取值。
14.(重慶卷11)設(shè)集合U={1,2,3,4,5},A={2,4},B={3,4,5},C={3,4},則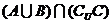 = .
= .
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com