
【題目】(2015·陜西)已知橢圓E: ![]() (a>b>0)的半焦距為c,原點(diǎn)0到經(jīng)過(guò)兩點(diǎn)(c,0),(0,b)的直線的距離為
(a>b>0)的半焦距為c,原點(diǎn)0到經(jīng)過(guò)兩點(diǎn)(c,0),(0,b)的直線的距離為![]() c.
c.
(1)求橢圓E的離心率
(2)如圖,AB是圓M:(x+2)2+(y-1)=![]() 的一條直徑,若橢圓E經(jīng)過(guò)A,B兩點(diǎn),求橢圓E的方程.
的一條直徑,若橢圓E經(jīng)過(guò)A,B兩點(diǎn),求橢圓E的方程.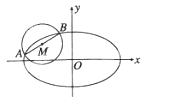
【答案】
(1)
![]()
(2)
![]()
【解析】先寫(xiě)過(guò)點(diǎn)(c,0),(0,b)的直線方程,再計(jì)算原點(diǎn)o到該直線的距離,進(jìn)而可得橢圓E的離心率;(II)先由(I)知橢圓E的方程,設(shè)AB的方程,聯(lián)立![]() ,消去y,可得x1+x2和x1x2的值,進(jìn)而可得k,再利用|AB|=
,消去y,可得x1+x2和x1x2的值,進(jìn)而可得k,再利用|AB|=![]() 可得b2的值,進(jìn)而可得橢圓E的方程.
可得b2的值,進(jìn)而可得橢圓E的方程.
試題解析:(I)過(guò)點(diǎn)(c,0),(0,b)的直線方程為bx+cy-bc=0,
則原點(diǎn)O到直線的距離d=![]() ,
,
由d=![]() ,得a=2b=2
,得a=2b=2![]() ,解得離心率
,解得離心率![]() =
=![]() .
.
(II)解法一:由(I)知,橢圓E的方程為.x2+4y2=4b2(1)
依題意,圓心M(-2,1)是線段AB的中點(diǎn),且|AB|=![]() .
.
易知,AB不與x軸垂直,設(shè)其直線方程為y=k(x+2)+1,代入(1)得
(1+4k2)x2+8k(2k+1)x+4(2k+1)2-4b2=0
設(shè)A(x1,y1), B (x2, y2 ) 則x1+x2=-![]() , x1·x2=-
, x1·x2=-![]()
由x1+x2=-4,得=![]() =-4解得k=
=-4解得k=![]()
從而.x1·x2=8-2b2.
于是.|AB|=![]() |x1-x2|=
|x1-x2|=![]()
![]() =
=![]()
由|AB|=![]() ,得
,得![]() =
=![]() ,解得b2=3
,解得b2=3
故橢圓E的方程為![]()
解法二:由(I)知,橢圓E的方程為x2+4y2=4b2. (2)
依題意,點(diǎn)A,B關(guān)于圓心M(-2,1)對(duì)稱,且|AB|=![]() .
.
設(shè)A(x1,y1), B (x2, y2 )則,x12+4y12=4b2 , x22+y22=4b2
兩式相減并結(jié)合x(chóng)1+x2=-4, y1+y2=2得-4(x1-x2)+8(y1-y2)=0.
易知,AB不與x軸垂直,則x1≠x2 , 所以AB的斜率kAB=![]() =
=![]()
因此AB直線方程為y=![]() (x+2)+1,代入(2)得x2+4x+8-2b2=0
(x+2)+1,代入(2)得x2+4x+8-2b2=0
所以,x1+x2=-4, x1·x2=8-2b2.
于是.|AB|=![]() |x1-x2|=
|x1-x2|=![]()
![]() =
=![]()
由|AB|=![]() ,得
,得![]() =
=![]() ,解得b2=3.
,解得b2=3.
故橢圓E的方程為![]() .
.


 狀元坊全程突破導(dǎo)練測(cè)系列答案
狀元坊全程突破導(dǎo)練測(cè)系列答案 直通貴州名校周測(cè)月考直通名校系列答案
直通貴州名校周測(cè)月考直通名校系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,已知![]() 平面
平面![]() ,點(diǎn)
,點(diǎn)![]() 分別是
分別是![]() 的中點(diǎn)。
的中點(diǎn)。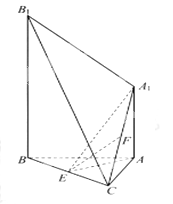
(1)求證:![]()
![]() 平面
平面![]()
(2)求證:平面![]() 平面
平面![]()
(3)求直線![]() 與平面
與平面![]() 所成角的大小
所成角的大小
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知橢圓![]() 的左焦點(diǎn)為
的左焦點(diǎn)為![]() ,離心率為
,離心率為![]() , 點(diǎn)
, 點(diǎn)![]() 在橢圓上且位于第一象限,直線
在橢圓上且位于第一象限,直線![]() 被圓
被圓![]() 截得的線段的長(zhǎng)為
截得的線段的長(zhǎng)為![]() .(1)求直線 F M 的斜率(2)求橢圓的方程(3)設(shè)動(dòng)點(diǎn) P 在橢圓上,若直線FP的斜率大于
.(1)求直線 F M 的斜率(2)求橢圓的方程(3)設(shè)動(dòng)點(diǎn) P 在橢圓上,若直線FP的斜率大于![]() ,求直線OP( O 為原點(diǎn))的斜率的取值范圍
,求直線OP( O 為原點(diǎn))的斜率的取值范圍
(1)求直線![]() 的斜率
的斜率
(2)求橢圓的方程
(3)設(shè)動(dòng)點(diǎn)![]() 在橢圓上,若直線
在橢圓上,若直線![]() 的斜率大于
的斜率大于![]() , 求直線
, 求直線![]() (
(![]() 為原點(diǎn))的斜率的取值范圍
為原點(diǎn))的斜率的取值范圍
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】![]() 設(shè)
設(shè)![]() ,Xn是曲線y=X2n+2+1在點(diǎn)(1,2)處的切線與x軸焦點(diǎn)的橫坐標(biāo)
,Xn是曲線y=X2n+2+1在點(diǎn)(1,2)處的切線與x軸焦點(diǎn)的橫坐標(biāo)
(1)求數(shù)列{xn}的通項(xiàng)公式;
(2)記Tn=![]()
![]() ....
....![]() ,證明Tn
,證明Tn![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】(2015·陜西)如圖,一橫截面為等腰梯形的水渠,因泥沙沉積,導(dǎo)致水渠截面邊界呈拋物線型(圖中虛線表示),則原始的最大流量與當(dāng)前最大流量的比值為 .
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】
設(shè)函數(shù)![]()
①若![]() ,則
,則![]() 的最小值為 ;
的最小值為 ;
②若![]() 恰有2個(gè)零點(diǎn),則實(shí)數(shù)
恰有2個(gè)零點(diǎn),則實(shí)數(shù)![]() 的取值范圍是 .
的取值范圍是 .
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在一次馬拉松比賽中,35名運(yùn)動(dòng)員的成績(jī)(單位:分鐘)的莖葉圖如圖所示,若將運(yùn)動(dòng)員按成績(jī)由好到差編為![]() 號(hào),再用系統(tǒng)抽樣方法從中抽取7人,則其中成績(jī)?cè)趨^(qū)間
號(hào),再用系統(tǒng)抽樣方法從中抽取7人,則其中成績(jī)?cè)趨^(qū)間![]() 上的運(yùn)動(dòng)員人數(shù)是
上的運(yùn)動(dòng)員人數(shù)是 
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)函數(shù)f(x)=|x+ ![]() |+|x﹣a|(a>0).
|+|x﹣a|(a>0).
(1)證明:f(x)≥2;
(2)若f(3)<5,求a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在等差數(shù)列{an}中,a1=﹣2,a12=20. (Ⅰ)求通項(xiàng)an;
(Ⅱ)若 ![]() ,求數(shù)列
,求數(shù)列 ![]() 的前n項(xiàng)和.
的前n項(xiàng)和.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com