
【題目】已知函數(shù)f(x)= ![]()
(1)計算f(1)+f(0)的值;
(2)計算f(x)+f(1﹣x)的值;
(3)若關于x的不等式:f[23x﹣2﹣x+m(2x﹣2﹣x)+ ![]() ]<
]< ![]() 在區(qū)間[1,2]上有解,求實數(shù)m的取值范圍.
在區(qū)間[1,2]上有解,求實數(shù)m的取值范圍.
【答案】
(1)解:∵f(x)= ![]()
∴f(1)+f(0)= ![]() +
+ ![]()
= ![]() +
+ ![]()
=2﹣ ![]()
=1
(2)解:f(x)+f(1﹣x)
= ![]()
= ![]() =1
=1
(3)解:∵f(x)= ![]() =
= ![]() ,
,
∴f(x)在[1,2]上單調遞增,
∵f( ![]() )=
)= ![]() =
= ![]() ,
,
∴f[ ![]() ]<
]< ![]() =f(
=f( ![]() ),
),
∵f(x)在[1,2]上單調遞增,
∴23x﹣2﹣x+m(2x﹣2﹣x)+ ![]() ,
,
∴23x﹣2﹣x+m(2x﹣2﹣x)<0,
∴m<﹣ ![]() =
= ![]() =﹣(22x+1),
=﹣(22x+1),
當x=1時,﹣(22x+1)max=﹣5.
∴m<﹣5.
∴實數(shù)m的取值范圍(﹣∞,﹣5)
【解析】(1)根據(jù)函數(shù)的解析式直接計算f(1)+f(0)的值.(2)根據(jù)函數(shù)的解析式直接計算f(x)+f(1﹣x)的值.(3)推導出f(x)在[1,2)上單調遞增,從而得到23x﹣2﹣x+m(2x﹣2﹣x)<0,由此能求出實數(shù)m的取值范圍.
【考點精析】利用函數(shù)的值對題目進行判斷即可得到答案,需要熟知函數(shù)值的求法:①配方法(二次或四次);②“判別式法”;③反函數(shù)法;④換元法;⑤不等式法;⑥函數(shù)的單調性法.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學 來源: 題型:
【題目】設點![]() 是棱長為2的正方體
是棱長為2的正方體![]() 的棱
的棱![]() 的中點,點
的中點,點![]() 在面
在面![]() 所在的平面內,若平面
所在的平面內,若平面![]() 分別與平面
分別與平面![]() 和平面
和平面![]() 所成的銳二面角相等,則點
所成的銳二面角相等,則點![]() 到點
到點![]() 的最短距離是( )
的最短距離是( )
A. ![]() B.
B. ![]() C. 1 D.
C. 1 D. ![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某商場在店慶一周年開展“購物折上折活動”:商場內所有商品按標價的八折出售,折后價格每滿500元再減100元.如某商品標價為1500元,則購買該商品的實際付款額為1500×0.8﹣200=1000(元).設購買某商品得到的實際折扣率= ![]() .設某商品標價為x元,購買該商品得到的實際折扣率為y.
.設某商品標價為x元,購買該商品得到的實際折扣率為y.
(1)寫出當x∈(0,1000]時,y關于x的函數(shù)解析式,并求出購買標價為1000元商品得到的實際折扣率;
(2)對于標價在[2500,3500]的商品,顧客購買標價為多少元的商品,可得到的實際折扣率低于 ![]() ?
?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)),以坐標原點為極點,
為參數(shù)),以坐標原點為極點, ![]() 軸的正半軸為極軸建立極坐標系,直線
軸的正半軸為極軸建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)寫出![]() 的直角坐標方程,并且用
的直角坐標方程,并且用![]() (
(![]() 為直線的傾斜角,
為直線的傾斜角, ![]() 為參數(shù))的形式寫出直線
為參數(shù))的形式寫出直線![]() 的一個參數(shù)方程;
的一個參數(shù)方程;
(2) ![]() 與
與![]() 是否相交,若相交求出兩交點的距離,若不相交,請說明理由.
是否相交,若相交求出兩交點的距離,若不相交,請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某高校學生社團為了解“大數(shù)據(jù)時代”下大學生就業(yè)情況的滿意度,對20名學生進行問卷計分調查(滿分100分),得到如圖所示的莖葉圖:
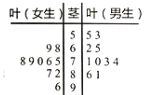
(1)計算男生打分的平均分,觀察莖葉圖,評價男女生打分的分散程度;
(2)從打分在80分以上的同學隨機抽3人,求被抽到的女生人數(shù)![]() 的分布列和數(shù)學期望.
的分布列和數(shù)學期望.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】有甲、乙兩個班級進行數(shù)學考試,按照大于或等于90分為優(yōu)秀,90分以下為非優(yōu)秀統(tǒng)計成績后,得到如表的列聯(lián)表.
優(yōu)秀 | 非優(yōu)秀 | 總計 | |
甲班 | 10 | ||
乙班 | 30 | ||
合計 | 100 |
已知在全部100人中抽到隨機抽取1人為優(yōu)秀的概率為 ![]() .
.
(1)請完成如表的列聯(lián)表;
(2)根據(jù)列聯(lián)表的數(shù)據(jù),有多大的把握認為“成績與班級有關系“?
(3)按分層抽樣的方法,從優(yōu)秀學生中抽出6名組成一個樣本,再從樣本中抽出2名學生,求恰好有1個學生在甲班的概率.
參考公式和數(shù)據(jù):K2= ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
下面的臨界值表供參考:
p(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,四邊形PDCE為矩形,四邊形ABCD為梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD= ![]() CD=a,PD=
CD=a,PD= ![]() a.
a. 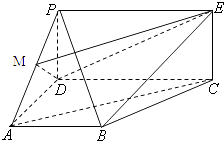
(1)若M為PA中點,求證:AC∥平面MDE;
(2)求平面PAD與PBC所成銳二面角的大小.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】規(guī)定投擲飛鏢3次為一輪,若3次中至少兩次投中8環(huán)以上為優(yōu)秀,現(xiàn)采用隨機模擬實驗的方法估計某人投擲飛鏢的情況:先由計算器產生隨機數(shù)0或1,用0表示該次投標未在8環(huán)以上,用1表示該次投標在8環(huán)以上;再以每三個隨機數(shù)作為一組,代表一輪的結果,經隨機模擬實驗產生了如下20組隨機數(shù):
101 111 011 101 010 100 100 011 111 110
000 011 010 001 111 011 100 000 101 101
據(jù)此估計,該選手投擲飛鏢三輪,至少有一輪可以拿到優(yōu)秀的概率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com