
【題目】如圖,四邊形PDCE為矩形,四邊形ABCD為梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD= ![]() CD=a,PD=
CD=a,PD= ![]() a.
a. 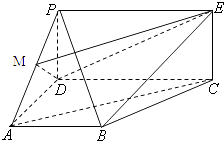
(1)若M為PA中點,求證:AC∥平面MDE;
(2)求平面PAD與PBC所成銳二面角的大小.
【答案】
(1)解:證明:連接PC,交DE與N,連接MN,
在△PAC中,∵M,N分別為兩腰PA,PC的中點
∴MN∥AC,
又AC面MDE,MN面MDE,
所以 AC∥平面MDE
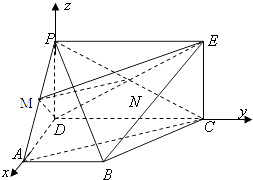
(2)解:以D為空間坐標系的原點,分別以 DA,DC,DP所在直線為x,y,z軸建立空間直角坐標系,
則P(0,0, ![]() a),B(a,a,0),C(0,2a,0),
a),B(a,a,0),C(0,2a,0),
所以 ![]() ,
, ![]() ,
,
設平面PAD的單位法向量為 ![]() ,則可取
,則可取 ![]()
設面PBC的法向量 ![]() ,
,
則有 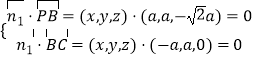
即: ![]() ,取z=1,
,取z=1,
則 ![]() ∴
∴ ![]()
設平面PAD與平面PBC所成銳二面角的大小為θ,
∴ 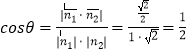
∴θ=60°,
所以平面PAD與平面PBC所成銳二面角的大小為60°
【解析】(1)連接PC,交DE與N,連接MN,所以MN∥AC,再根據線面平行的判定定理可得答案.(2)以D為空間坐標系的原點,分別以 DA,DC,DP所在直線為x,y,z軸建立空間直角坐標系,分別求出兩個平面的法向量,再求出兩個向量的夾角,進而轉化為二面角的平面角.


 金博士一點全通系列答案
金博士一點全通系列答案科目:高中數學 來源: 題型:
【題目】已知f(x)=log2(2x+a)的定義域為(0,+∞).
(1)求a的值;
(2)若g(x)=log2(2x+1),且關于x的方程f(x)=m+g(x)在[1,2]上有解,求m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知四棱錐中,PA⊥平面ABCD,底面ABCD是邊長為a的菱形,∠BAD=120°,PA=b. 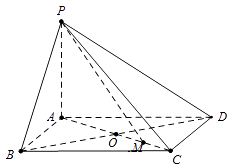
(1)求證:平面PBD⊥平面PAC;
(2)設AC與BD交于點O,M為OC中點,若二面角O﹣PM﹣D的正切值為2 ![]() ,求a:b的值.
,求a:b的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]()
(1)計算f(1)+f(0)的值;
(2)計算f(x)+f(1﹣x)的值;
(3)若關于x的不等式:f[23x﹣2﹣x+m(2x﹣2﹣x)+ ![]() ]<
]< ![]() 在區間[1,2]上有解,求實數m的取值范圍.
在區間[1,2]上有解,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數y=x+ ![]() 有如下性質:如果常數t>0,那么該函數在
有如下性質:如果常數t>0,那么該函數在 ![]() 上是減函數,在
上是減函數,在 ![]() 上是增函數.
上是增函數.
(1)已知f(x)= ![]() ,x∈[﹣1,1],利用上述性質,求函數f(x)的單調區間和值域;
,x∈[﹣1,1],利用上述性質,求函數f(x)的單調區間和值域;
(2)對于(1)中的函數f(x)和函數g(x)=﹣x﹣2a,若對任意x1∈[﹣1,1],總存在x2∈[0,1],使得g(x2)=f(x1)成立,求實數a的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知冪函數f(x)=xa的圖象經過點( ![]() ,
, ![]() ).
).
(1)求函數f(x)的解析式,并判斷奇偶性;
(2)判斷函數f(x)在(﹣∞,0)上的單調性,并用單調性定義證明.
(3)作出函數f(x)在定義域內的大致圖象(不必寫出作圖過程).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知全集U={1,2,3,4},集合A={1,2,x2}與B={1,4}是它的子集,
(1)求UB;
(2)若A∩B=B,求x的值;
(3)若A∪B=U,求x.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com