
數(shù)列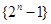 的前
的前 項(xiàng)組成集合
項(xiàng)組成集合 ,從集合
,從集合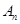 中任取
中任取 個(gè)數(shù),其所有可能的
個(gè)數(shù),其所有可能的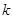 個(gè)數(shù)的乘積的和為
個(gè)數(shù)的乘積的和為 (若只取一個(gè)數(shù),規(guī)定乘積為此數(shù)本身),記
(若只取一個(gè)數(shù),規(guī)定乘積為此數(shù)本身),記 .例如:當(dāng)
.例如:當(dāng) 時(shí),
時(shí), ,
, ,
, ;當(dāng)
;當(dāng) 時(shí),
時(shí), ,
, ,
, .
.
(Ⅰ)求 ;
;
(Ⅱ)猜想 ,并用數(shù)學(xué)歸納法證明.
,并用數(shù)學(xué)歸納法證明.
(Ⅰ)63; (Ⅱ) .
.
解析試題分析:(Ⅰ)通過(guò)列舉進(jìn)行計(jì)算;(Ⅱ)先從特殊入手,
當(dāng) 時(shí),
時(shí), ,
, ,
, ;
;
當(dāng) 時(shí),
時(shí), ,
, ,
, ,所以
,所以 ;
;
從特殊到一般探求 與
與 之間的遞推關(guān)系,從而便于用數(shù)學(xué)歸納法證明.
之間的遞推關(guān)系,從而便于用數(shù)學(xué)歸納法證明.
試題解析:(Ⅰ)當(dāng) 時(shí),
時(shí), ,
, ,
, ,所以
,所以 ;
;
(Ⅱ)由 ,
,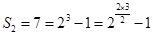 ,
,
猜想 ,下面證明:
,下面證明:
(1)易知 時(shí)成立;
時(shí)成立;
(2)假設(shè) 時(shí)
時(shí) ,
,
則 時(shí),
時(shí),

(其中 ,為
,為 時(shí)可能的
時(shí)可能的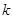 個(gè)數(shù)的乘積的和為
個(gè)數(shù)的乘積的和為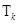 ),
),




即 時(shí)
時(shí) 也成立,
也成立,
綜合(1)(2)知對(duì) ,
, 成立.
成立.
所以 .
.
考點(diǎn):歸納推理、數(shù)學(xué)歸納法.


 教育世家狀元卷系列答案
教育世家狀元卷系列答案 黃岡課堂作業(yè)本系列答案
黃岡課堂作業(yè)本系列答案 單元加期末復(fù)習(xí)先鋒大考卷系列答案
單元加期末復(fù)習(xí)先鋒大考卷系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
設(shè) 是一個(gè)自然數(shù),
是一個(gè)自然數(shù), 是
是 的各位數(shù)字的平方和,定義數(shù)列
的各位數(shù)字的平方和,定義數(shù)列 :
: 是自然數(shù),
是自然數(shù), (
( ,
, ).
).
(1)求 ,
, ;
;
(2)若 ,求證:
,求證: ;
;
(3)求證:存在 ,使得
,使得 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
某同學(xué)在一次研究性學(xué)習(xí)中發(fā)現(xiàn),以下五個(gè)式子的值都等于同一個(gè)常數(shù).
(1)sin213°+cos217°-sin 13°cos 17°.
(2)sin215°+cos215°-sin 15°cos 15°.
(3)sin218°+cos212°-sin 18°cos 12°.
(4)sin2(-18°)+cos248°-sin(-18°)cos 48°.
(5)sin2(-25°)+cos255°-sin(-25°)cos 55°.
①試從上述五個(gè)式子中選擇一個(gè),求出這個(gè)常數(shù).
②根據(jù)①的計(jì)算結(jié)果,將該同學(xué)的發(fā)現(xiàn)推廣為三角恒等式,并證明你的結(jié)論.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知Sn為正項(xiàng)數(shù)列{an}的前n項(xiàng)和,且滿足Sn=
 +
+ an(n∈
an(n∈
N+),求出a1,a2,a3,a4,猜想{an}的通項(xiàng)公式并給出證明
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知多項(xiàng)式f(n)= n5+
n5+ n4+
n4+ n3-
n3- n.
n.
(1)求f(-1)及f(2)的值;
(2)試探求對(duì)一切整數(shù)n,f(n)是否一定是整數(shù)?并證明你的結(jié)論.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知 ,考查
,考查
①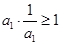 ;
;
② ;
;
③ .
.
歸納出對(duì) 都成立的類(lèi)似不等式,并用數(shù)學(xué)歸納法加以證明.
都成立的類(lèi)似不等式,并用數(shù)學(xué)歸納法加以證明.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:單選題
投擲兩顆骰子,得到其向上的點(diǎn)數(shù)分別為m和n,則復(fù)數(shù)(m+ni)(n﹣mi)為實(shí)數(shù)的概率為( )
A. | B. | C. | D. |
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com