
【題目】給定一個數列{an},在這個數列里,任取m(m≥3,m∈N*)項,并且不改變它們在數列{an}中的先后次序,得到的數列{an}的一個m階子數列.
已知數列{an}的通項公式為an= ![]() (n∈N* , a為常數),等差數列a2 , a3 , a6是數列{an}的一個3子階數列.
(n∈N* , a為常數),等差數列a2 , a3 , a6是數列{an}的一個3子階數列.
(1)求a的值;
(2)等差數列b1 , b2 , …,bm是{an}的一個m(m≥3,m∈N*)階子數列,且b1= ![]() (k為常數,k∈N* , k≥2),求證:m≤k+1
(k為常數,k∈N* , k≥2),求證:m≤k+1
(3)等比數列c1 , c2 , …,cm是{an}的一個m(m≥3,m∈N*)階子數列,求證:c1+c1+…+cm≤2﹣ ![]() .
.
【答案】
(1)解:∵a2,a3,a6成等差數列,
∴a2﹣a3=a3﹣a6.
又∵a2= ![]() ,a3=
,a3= ![]() ,a6=
,a6= ![]() ,
,
代入得 ![]() ﹣
﹣ ![]() =
= ![]() ﹣
﹣ ![]() ,解得a=0
,解得a=0
(2)證明:設等差數列b1,b2,…,bm的公差為d.
∵b1= ![]() ,∴b2≤
,∴b2≤ ![]() ,
,
從而d=b2﹣b1≤ ![]() ﹣
﹣ ![]() =﹣
=﹣ ![]() .
.
∴bm=b1+(m﹣1)d≤ ![]() ﹣
﹣ ![]() .
.
又∵bm>0,∴ ![]() ﹣
﹣ ![]() >0.
>0.
即m﹣1<k+1.
∴m<k+2.
又∵m,k∈N*,∴m≤k+1.
(3)證明:設c1= ![]() (t∈N*),等比數列c1,c2,…,cm的公比為q.
(t∈N*),等比數列c1,c2,…,cm的公比為q.
∵c2≤ ![]() ,∴q=
,∴q= ![]() ≤
≤ ![]() .
.
從而cn=c1qn﹣1≤ ![]() (1≤n≤m,n∈N*).
(1≤n≤m,n∈N*).
∴c1+c2+…+cm≤ ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]()
= ![]() ,
,
設函數f(x)=x﹣ ![]() ,(m≥3,m∈N*).
,(m≥3,m∈N*).
當x∈(0,+∞)時,函數f(x)=x﹣ ![]() 為單調增函數.
為單調增函數.
∵當t∈N*,∴1< ![]() ≤2.∴f(
≤2.∴f( ![]() )≤2﹣
)≤2﹣ ![]() .
.
即 c1+c2+…+cm≤2﹣ ![]() .
.
【解析】(1)利用等差數列的定義及其性質即可得出;(2)設等差數列b1 , b2 , …,bm的公差為d.由b1= ![]() ,可得b2≤
,可得b2≤ ![]() ,再利用等差數列的通項公式及其不等式的性質即可證明;(3)設c1=
,再利用等差數列的通項公式及其不等式的性質即可證明;(3)設c1= ![]() (t∈N*),等比數列c1 , c2 , …,cm的公比為q.由c2≤
(t∈N*),等比數列c1 , c2 , …,cm的公比為q.由c2≤ ![]() ,可得q=
,可得q= ![]() ≤
≤ ![]() .從而cn=c1qn﹣1≤
.從而cn=c1qn﹣1≤ ![]() (1≤n≤m,n∈N*).再利用等比數列的前n項和公式、函數的單調性即可得出.
(1≤n≤m,n∈N*).再利用等比數列的前n項和公式、函數的單調性即可得出.
【考點精析】通過靈活運用數列的前n項和和等差數列的性質,掌握數列{an}的前n項和sn與通項an的關系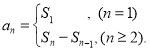 ;在等差數列{an}中,從第2項起,每一項是它相鄰二項的等差中項;相隔等距離的項組成的數列是等差數列即可以解答此題.
;在等差數列{an}中,從第2項起,每一項是它相鄰二項的等差中項;相隔等距離的項組成的數列是等差數列即可以解答此題.


科目:高中數學 來源: 題型:
【題目】已知二次函數![]() ,則下列說法不正確的是( )
,則下列說法不正確的是( )
A.其圖象開口向上,且始終與![]() 軸有兩個不同的交點
軸有兩個不同的交點
B.無論![]() 取何實數,其圖象始終過定點
取何實數,其圖象始終過定點![]()
C.其圖象對稱軸的位置沒有確定,但其形狀不會因![]() 的取值不同而改變
的取值不同而改變
D.函數的最小值大于![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將5名報名參加運動會的同學分別安排到跳繩、接力,投籃三項比賽中(假設這些比賽都不設人數上限),每人只參加一項,則共有![]() 種不同的方案;若每項比賽至少要安排一人時,則共有
種不同的方案;若每項比賽至少要安排一人時,則共有![]() 種不同的方案,其中
種不同的方案,其中![]() 的值為( )
的值為( )
A. 543 B. 425 C. 393 D. 275
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在四棱錐P﹣ABCD中,側面PCD⊥底面ABCD,PD⊥CD,E為PC中點,底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=AD=PD=1,CD=2. 
(1)求證:BE∥平面PAD;
(2)求證:BC⊥平面PBD;
(3)在線段PC上是否存在一點Q,使得二面角Q﹣BD﹣P為45°?若存在,求 ![]() 的值;若不存在,請述明理由.
的值;若不存在,請述明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的離心率
的離心率![]() ,該橢圓中心到直線
,該橢圓中心到直線![]() 的距離為
的距離為![]() .
.
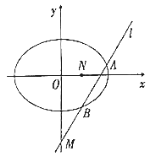
(1)求橢圓![]() 的方程;
的方程;
(2)是否存在過點![]() 的直線
的直線![]() ,使直線
,使直線![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
,![]() 兩點,且以
兩點,且以![]() 為直徑的圓過定點
為直徑的圓過定點![]() ?若存在,求出所有符合條件的直線方程;若不存在,請說明理由.
?若存在,求出所有符合條件的直線方程;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=log4(ax2+2x+3).
(1)若f(1)=1,求f(x)的單調區間;
(2)是否存在實數a,使f(x)的最小值為0?若存在,求出a的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)=﹣ex+ex(e為自然對數的底數)
(1)求函數f(x)的最大值;
(2)設g(x)=lnx+ ![]() x2+ax,若對任意x1∈(0,2],總存在x2∈(0,2].使得g(x1)<f(x2),求實數a的取值范圍.
x2+ax,若對任意x1∈(0,2],總存在x2∈(0,2].使得g(x1)<f(x2),求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在一次購物抽獎活動中,假設某10張券中有一等獎券1張,可獲價值50元的獎品;有二等獎券3張,每張可獲價值10元的獎品;其余6張沒有獎,某顧客從此10張券中任抽2張,求:
(1)該顧客中獎的概率;
(2)該顧客獲得的獎品總價值X(元)的概率分布列和期望E(X).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com