Question

【題目】已知橢圓：的離心率，該橢圓中心到直線的距離為.

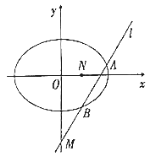
（1）求橢圓的方程；

（2）是否存在過點的直線，使直線與橢圓交于，兩點，且以為直徑的圓過定點？若存在，求出所有符合條件的直線方程；若不存在，請說明理由.

Answer 1

【答案】(1) .

(2) 存在直線：或：，使得以為直徑的圓經過點.

【解析】分析：由，該橢圓中心到直線的距離為，求出橢圓方程；

（2）先假設存在這樣的直線，設出直線方程（注意考慮斜率），與橢圓聯立，考慮然后設，，利用韋達定理，利用為直徑的圓過定點，轉化，轉化坐標構造方程進行求解。

詳解：（1）直線的一般方程為，

依題意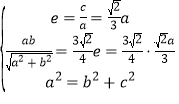得，解得，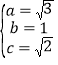

所以橢圓的方程為.

（2）當直線的斜率不存在時，直線即為軸，此時，為橢圓的短軸端點，以為直徑的圓經過點.

當直線的斜率存在時，設其斜率為，由，

得.

所以，得.

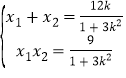設，，則，①

而 .

因為以為直徑的圓過定點，所以，則，即.

所以.②

將①式代入②式整理解得.

綜上可知，存在直線：或：，使得以為直徑的圓經過點.

點晴：本題考查直線與橢圓的位置關系，這類題目一般涉及設直線方程，然后和橢圓聯立，設點，考慮，然后利用韋達定理，接下來就是對題干的轉化啦，本題中典型的垂直問題，主要轉化方向就是向量點乘，因為斜率的話還需要考慮斜率是否存在。