
【題目】已知f(x)=﹣ex+ex(e為自然對數(shù)的底數(shù))
(1)求函數(shù)f(x)的最大值;
(2)設(shè)g(x)=lnx+ ![]() x2+ax,若對任意x1∈(0,2],總存在x2∈(0,2].使得g(x1)<f(x2),求實數(shù)a的取值范圍.
x2+ax,若對任意x1∈(0,2],總存在x2∈(0,2].使得g(x1)<f(x2),求實數(shù)a的取值范圍.
【答案】
(1)解:f(x)=﹣ex+ex的導(dǎo)數(shù)為f′(x)=﹣ex+e,
當(dāng)x∈(﹣∞,1)時,f′(x)>0,f(x)單調(diào)遞增;
當(dāng)x∈(1,+∞)時,f′(x)<0,f(x)單調(diào)遞減;
故f(x)max=f(1)=0;
(2)解:對任意x1∈(0,2],總存在x2∈(0,2],
使得g(x1)<f(x2)等價于g(x1)<f(x2)max.
由(1)可知f(x2)max=f(1)=0.
問題轉(zhuǎn)化為g(x)<0在x∈(0,2]恒成立.
參變量分離得:﹣a> ![]() =
= ![]() +
+ ![]() x,
x,
令r(x)= ![]() +
+ ![]() x,x∈(0,2],
x,x∈(0,2],
r′(x)= ![]() +
+ ![]() ,由0<x≤2時,1﹣lnx>0,得r′(x)>0,
,由0<x≤2時,1﹣lnx>0,得r′(x)>0,
即r(x)在x1∈(0,2]上單增.
故﹣a>r(x)max=r(2)= ![]() +1.
+1.
綜上:a<﹣ ![]() ﹣1,
﹣1,
即a的取值范圍為 (﹣∞,﹣ ![]() ﹣1).
﹣1).
【解析】(1)求得f(x)的導(dǎo)數(shù),由導(dǎo)數(shù)大于0,可得增區(qū)間;導(dǎo)數(shù)小于0,可得減區(qū)間,進而得到函數(shù)f(x)的最大值;(2)由題意可得g(x1)<f(x2)max . 由(Ⅰ)可得問題轉(zhuǎn)化為g(x)<0在x∈(0,2]恒成立.運用參數(shù)分離,求得不等式右邊函數(shù)的最大值,即可得到所求a的范圍.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)![]() 是定義為R的偶函數(shù),且
是定義為R的偶函數(shù),且![]() 對任意的
對任意的![]() ,都有
,都有![]() 且當(dāng)
且當(dāng)![]() 時,
時, ![]() ,若在區(qū)間
,若在區(qū)間![]() 內(nèi)關(guān)于
內(nèi)關(guān)于![]() 的方程
的方程![]() 恰好有3個不同的實數(shù)根,則
恰好有3個不同的實數(shù)根,則![]() 的取值范圍是 ( )
的取值范圍是 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】給定一個數(shù)列{an},在這個數(shù)列里,任取m(m≥3,m∈N*)項,并且不改變它們在數(shù)列{an}中的先后次序,得到的數(shù)列{an}的一個m階子數(shù)列.
已知數(shù)列{an}的通項公式為an= ![]() (n∈N* , a為常數(shù)),等差數(shù)列a2 , a3 , a6是數(shù)列{an}的一個3子階數(shù)列.
(n∈N* , a為常數(shù)),等差數(shù)列a2 , a3 , a6是數(shù)列{an}的一個3子階數(shù)列.
(1)求a的值;
(2)等差數(shù)列b1 , b2 , …,bm是{an}的一個m(m≥3,m∈N*)階子數(shù)列,且b1= ![]() (k為常數(shù),k∈N* , k≥2),求證:m≤k+1
(k為常數(shù),k∈N* , k≥2),求證:m≤k+1
(3)等比數(shù)列c1 , c2 , …,cm是{an}的一個m(m≥3,m∈N*)階子數(shù)列,求證:c1+c1+…+cm≤2﹣ ![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)列{an}的前n項和Sn= ![]() ﹣
﹣ ![]() (n∈N*).
(n∈N*).
(1)求數(shù)列{an}的通項公式;
(2)若bn=anlog3an , 求數(shù)列{bn}的前n項和.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在中學(xué)生綜合素質(zhì)評價某個維度的測評中,分優(yōu)秀、合格、尚待改進三個等級進行學(xué)生互評.某校高一年級有男生500人,女生400人,為了了解性別對該維度測評結(jié)果的影響,采用分層抽樣方法從高一年級抽取了45名學(xué)生的測評結(jié)果,并作出頻數(shù)統(tǒng)計表如下:
表一:男生

表二:女生

(1)從表二的非優(yōu)秀學(xué)生中隨機抽取2人交談,求所選2人中恰有1人測評等級為合格的概率;
(2)由表中統(tǒng)計數(shù)據(jù)填寫下面的![]() 列聯(lián)表,并判斷是否有90%的把握認為“測評結(jié)果優(yōu)秀與性別有關(guān)”.
列聯(lián)表,并判斷是否有90%的把握認為“測評結(jié)果優(yōu)秀與性別有關(guān)”.

參考公式:  ,其中
,其中![]() .
.
參考數(shù)據(jù):
| 0.10 | 0.05 | 0.01 |
| 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某電腦公司有6名產(chǎn)品推銷員,其工作年限與推銷金額數(shù)據(jù)如下表:
推銷員編號 | 1 | 2 | 3 | 4 | 5 |
工作年限 | 3 | 5 | 6 | 7 | 9 |
推銷金額 | 2 | 3 | 3 | 4 | 5 |
(1)求年推銷金額![]() 關(guān)于工作年限
關(guān)于工作年限![]() 的線性回歸方程;
的線性回歸方程;
(2)若第6名推銷員的工作年限為11年,試估計他的年推銷金額.
附:線性回歸方程![]() 中,
中, ,
,![]() ,其中
,其中![]() 為樣本平均值.
為樣本平均值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知曲線![]() 為參數(shù)),
為參數(shù)),![]() 為參數(shù)).
為參數(shù)).
(1)化![]() 的參數(shù)方程為普通方程,并說明它們分別表示什么曲線;
的參數(shù)方程為普通方程,并說明它們分別表示什么曲線;
(2)若![]() 上的點
上的點![]() 對應(yīng)的參數(shù)為
對應(yīng)的參數(shù)為![]() 為
為![]() 上的動點,求
上的動點,求![]() 的中點
的中點![]() 到直線
到直線![]() 為參數(shù))距離的最小值.
為參數(shù))距離的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某電腦公司有6名產(chǎn)品推銷員,其工作年限與推銷金額數(shù)據(jù)如下表:
推銷員編號 | 1 | 2 | 3 | 4 | 5 |
工作年限 | 3 | 5 | 6 | 7 | 9 |
推銷金額 | 2 | 3 | 3 | 4 | 5 |
(1)求年推銷金額![]() 關(guān)于工作年限
關(guān)于工作年限![]() 的線性回歸方程;
的線性回歸方程;
(2)若第6名推銷員的工作年限為11年,試估計他的年推銷金額.
附:線性回歸方程![]() 中,
中,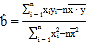 ,
,![]() ,其中
,其中![]() 為樣本平均值.
為樣本平均值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知向量 ![]() ,其中
,其中![]() .函數(shù)
.函數(shù)![]() 的圖象過點
的圖象過點![]() ,點
,點![]() 與其相鄰的最高點的距離為4.
與其相鄰的最高點的距離為4.
(Ⅰ)求函數(shù)![]() 的單調(diào)遞減區(qū)間;
的單調(diào)遞減區(qū)間;
(Ⅱ)計算![]() 的值;
的值;
(Ⅲ)設(shè)函數(shù)![]() ,試討論函數(shù)
,試討論函數(shù)![]() 在區(qū)間 [0,3] 上的零點個數(shù).
在區(qū)間 [0,3] 上的零點個數(shù).
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com