
【題目】橢圓C: ![]() 過點M(2,0),且右焦點為F(1,0),過F的直線l與橢圓C相交于A,B兩點.設點P(4,3),記PA,PB的斜率分別為k1和k2 .
過點M(2,0),且右焦點為F(1,0),過F的直線l與橢圓C相交于A,B兩點.設點P(4,3),記PA,PB的斜率分別為k1和k2 . 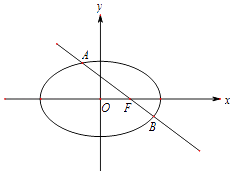
(1)求橢圓C的方程;
(2)如果直線l的斜率等于﹣1,求出k1k2的值;
(3)探討k1+k2是否為定值?如果是,求出該定值;如果不是,求出k1+k2的取值范圍.
【答案】
(1)
解:∵a=2,又c=1,∴ ![]() ,∴橢圓方程為
,∴橢圓方程為 ![]()
(2)
解:直線l:y=﹣x+1,設A(x1,y1)B(x2,y2),
由 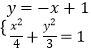 消y得7x2﹣8x﹣8=0,有
消y得7x2﹣8x﹣8=0,有 ![]() ,
, ![]()
![]()
(3)
解:當直線AB的斜率不存在時,不妨設A(1, ![]() ),B(1,﹣
),B(1,﹣ ![]() ),
),
則 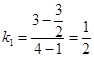 ,
, 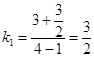 ,故k1+k2=2.
,故k1+k2=2.
當直線AB的斜率存在時,設其為k,則直線AB:y=k(x﹣1),設A(x1,y1)B(x2,y2),
由 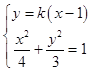 消y得(4k2+3)x2﹣8k2x+(4k2﹣12)=0,有
消y得(4k2+3)x2﹣8k2x+(4k2﹣12)=0,有 ![]() ,
, ![]()
![]()
= 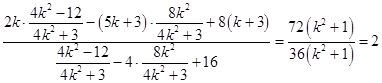
【解析】(1)利用已知條件求出b,即可求解橢圓方程.(2)直線l:y=﹣x+1,設AB坐標,聯立 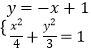 利用韋達定理以及斜率公式求解即可.(3)當直線AB的斜率不存在時,不妨設A,B,求出斜率,即可;當直線AB的斜率存在時,設其為k,求直線AB:y=k(x﹣1),聯立直線與橢圓的方程組,利用韋達定理以及斜率公式化簡求解即可.
利用韋達定理以及斜率公式求解即可.(3)當直線AB的斜率不存在時,不妨設A,B,求出斜率,即可;當直線AB的斜率存在時,設其為k,求直線AB:y=k(x﹣1),聯立直線與橢圓的方程組,利用韋達定理以及斜率公式化簡求解即可.


科目:高中數學 來源: 題型:
【題目】數列{an}的前n項a1 , a2 , …,an(n∈N*)組成集合An={a1 , a2 , …,an},從集合An中任取k(k=1,2,3,…,n)個數,其所有可能的k個數的乘積的和為Tk(若只取一個數,規定乘積為此數本身),例如:對于數列{2n﹣1},當n=1時,A1={1},T1=1;n=2時,A2={1,3},T1=1+3,T2=13;
(1)若集合An={1,3,5,…,2n﹣1},求當n=3時,T1 , T2 , T3的值;
(2)若集合An={1,3,7,…,2n﹣1},證明:n=k時集合Ak的Tm與n=k+1時集合Ak+1的Tm(為了以示區別,用Tm′表示)有關系式Tm′=(2k+1﹣1)Tm﹣1+Tm , 其中m,k∈N*,2≤m≤k;
(3)對于(2)中集合An . 定義Sn=T1+T2+…+Tn , 求Sn(用n表示).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如果一個數列從第2項起,每一項與它前一項的差都大于2,則稱這個數列為“H型數列”.
(1)若數列{an}為“H型數列”,且a1= ![]() ﹣3,a2=
﹣3,a2= ![]() ,a3=4,求實數m的取值范圍;
,a3=4,求實數m的取值范圍;
(2)是否存在首項為1的等差數列{an}為“H型數列”,且其前n項和Sn滿足Sn<n2+n(n∈N*)?若存在,請求出{an}的通項公式;若不存在,請說明理由.
(3)已知等比數列{an}的每一項均為正整數,且{an}為“H型數列”,bn= ![]() an , cn=
an , cn= ![]() ,當數列{bn}不是“H型數列”時,試判斷數列{cn}是否為“H型數列”,并說明理由.
,當數列{bn}不是“H型數列”時,試判斷數列{cn}是否為“H型數列”,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數列{an}是集合{x|x=3s+3t , s<t且s,t∈N}中所有的數從小到大排列成的數列,即a1=4,a2=10,a3=12,a4=28,a5=30,a6=36,…,將數列{an}中各項按照上小下大,左小右大的原則排成如圖的等腰直角三角形數表,則a15的值為 . 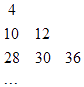
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義f(x)={x}(其中{x}表示不小于x的最小整數)為“取上整函數”,例如{2.1}=3,{4}=4.以下關于“取上整函數”性質的描述,正確的是( ) ①f(2x)=2f(x);
②若f(x1)=f(x2),則x1﹣x2<1;
③任意x1 , x2∈R,f(x1+x2)≤f(x1)+f(x2);
④ ![]() .
.
A.①②
B.①③
C.②③
D.②④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在正三棱柱ABC﹣A1B1C1中,AB=1,BB1=2,求: 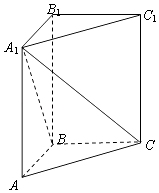
(1)異面直線B1C1與A1C所成角的大小;
(2)四棱錐A1﹣B1BCC1的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)=x2﹣ax+lnx,a∈R.
(1)當a=3時,求函數f(x)的極小值;
(2)令g(x)=x2﹣f(x),是否存在實數a,當x∈[1,e](e是自然對數的底數)時,函數g(x)取得最小值為1.若存在,求出a的值;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com