【題目】已知橢圓
的左，右焦點分別為
，直線
與橢圓
相交于
兩點；當(dāng)直線
經(jīng)過橢圓的下頂點
和右焦點
時，
的周長為
，且與橢圓的另一個交點的橫坐標為
（1）求橢圓的方程；
（2）點
為
內(nèi)一點，
為坐標原點，滿足
，若點恰好在圓
上，求實數(shù)
的取值范圍.
【答案】（1）
；（2）
或
【解析】
（1）由橢圓的定義可知，焦點三角形的周長為
，從而求出
.寫出直線
的方程，與橢圓方程聯(lián)立，根據(jù)交點橫坐標為
，求出
和
，從而寫出橢圓的方程；
（2）設(shè)出P、Q兩點坐標，由
可知點
為
的重心，根據(jù)重心坐標公式可將點用P、Q兩點坐標來表示.由點在圓O上，知點M的坐標滿足圓O的方程，得
式.
為直線l與橢圓
的兩個交點，用韋達定理表示
，將其代入方程，再利用
求得
的范圍，最終求出實數(shù)
的取值范圍.
解：（1）由題意知.
，
直線的方程為
∵直線與橢圓的另一個交點的橫坐標為
解得
或
(舍去)
，
∴橢圓的方程為
（2）設(shè)
.
∴點為的重心，
∵點在圓
上，
由
得 
，
代入方程，得
，
即
由得
解得
.
或
科目：高中數(shù)學(xué) 來源： 題型：
【題目】一個盒子里裝有
個均勻的紅球和
個均勻的白球，每個球被取到的概率相等，已知從盒子里一次隨機取出1個球，取到的球是紅球的概率為
，從盒子里一次隨機取出2個球，取到的球至少有1個是白球的概率為
.
（1）求，的值；
（2）若一次從盒子里隨機取出3個球，求取到的白球個數(shù)不小于紅球個數(shù)的概率.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖，在三棱錐P-ABC中，AC⊥BC，且，AC=BC=2，D，E分別為AB，PB中點，PD⊥平面ABC，PD=3.
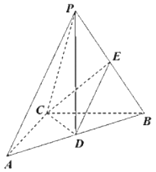
(1)求直線CE與直線PA夾角的余弦值；
(2)求直線PC與平面DEC夾角的正弦值.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】某市一所醫(yī)院在某時間段為發(fā)燒超過38
的病人特設(shè)發(fā)熱門診，該門診記錄了連續(xù)5天晝夜溫差
()與就診人數(shù)
的資料：
日期 | 第1天 | 第2天 | 第3天 | 第4天 | 第5天 |
晝夜溫差 | 8 | 10 | 13 | 12 | 7 |
就診人數(shù) | 18 | 25 | 28 | 27 | 17 |
(1)求
的相關(guān)系數(shù)
，并說明晝夜溫差()與就診人數(shù)具有很強的線性相關(guān)關(guān)系.
(2)求就診人數(shù)(人)關(guān)于出晝夜溫差
()的線性回歸方程，預(yù)測晝夜溫差為9時的就診人數(shù).
附：樣本
的相關(guān)系數(shù)為
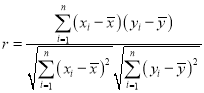，當(dāng)
時認為兩個變量有很強的線性相關(guān)關(guān)系.
回歸直線方程為
，其中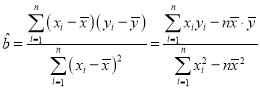
，
.
參考數(shù)據(jù)：
，
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知圓
，直線
．
（1）當(dāng)
時，直線
被圓
截得的弦長為__________；
（2）若在圓上存在一點
，在直線上存在一點
，使得
的中點恰為坐標原點
，則實數(shù)
的取值范圍是__________．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】在斜三棱柱
中，
是邊長為2的正三角形，側(cè)面
為菱形，且
，
，點O為AC中點．
（1）求證：
平面ABC；
（2）求直線
與平面
所成角的正弦值．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】下列命題：其中正確命題數(shù)是（ ）
A.在線性回歸模型中，相關(guān)系數(shù)
表示解釋變量
對于預(yù)報變量
變化的貢獻率，
越接近于1，表示回歸效果越好
B.兩個變量相關(guān)性越強，則相關(guān)系數(shù)的絕對值就越接近于1
C.在回歸直線方程
中，當(dāng)解釋變量每增加一個單位時，預(yù)報變量
平均減少0.5個單位
D.對分類變量
與
，它們的隨機變量
的觀測值來說，觀測值越小，“與有關(guān)系”的把握程度越大
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
，在點
處的切線方程為
，求（1）實數(shù)
的值；（2）函數(shù)
的單調(diào)區(qū)間以及在區(qū)間
上的最值.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知拋物線
的焦點
與橢圓
的右焦點重合，拋物線
的動弦
過點，過點且垂直于弦的直線交拋物線的準線于點
.
（Ⅰ）求拋物線的標準方程；
（Ⅱ）求
的最小值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
