Question

【題目】已知a+b+c=2，且a、b、c是正數，求證： + + ≥ ．

Answer 1

【答案】證明：a+b+c=2，且a、b、c是正數，
可得1= （2a+2b+2c），
+ + =（ + + ）×1
= （2a+2b+2c）（ + + ）
= [（a+b）+（b+c）+（c+a）]（ + + ）
≥ 3 3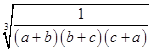
= （當且僅當a=b=c取得等號）．
則 + + ≥
【解析】由條件可得1= （2a+2b+2c），則 + + = （2a+2b+2c）（ + + ）= [（a+b）+（b+c）+（c+a）]（ + + ），再由三元基本不等式，以及不等式的可乘性，即可得證．
【考點精析】根據題目的已知條件，利用不等式的證明的相關知識可以得到問題的答案，需要掌握不等式證明的幾種常用方法:常用方法有：比較法（作差，作商法）、綜合法、分析法；其它方法有：換元法、反證法、放縮法、構造法，函數單調性法，數學歸納法等．