
【題目】一位網民在網上光顧某網店,經過一番瀏覽后,對該店鋪中的A,B,C三種商品有購買意向.已知該網民購買A種商品的概率為 ![]() ,購買B種商品的槪率為
,購買B種商品的槪率為 ![]() ,購買C種商品的概率為
,購買C種商品的概率為 ![]() .假設該網民是否購買這三種商品相互獨立
.假設該網民是否購買這三種商品相互獨立
(1)求該網民至少購買2種商品的概率;
(2)用隨機變量η表示該網民購買商品的種數,求η的槪率分布和數學期望.
【答案】
(1)解:記“記網民購買i種商品”為事件Ai,i=2,3,
則P(A3)= ![]() ,
,
P(A2)= ![]() +
+ ![]() =
= ![]() ,
,
∴該網民至少購買2種商品的概率:
p=p(A1)+P(A2)= ![]() =
= ![]()
(2)解:隨機變量η的可能取值為0,1,2,3,
P(η=0)=(1﹣ ![]() )×(1﹣
)×(1﹣ ![]() )×(1﹣
)×(1﹣ ![]() )=
)= ![]() ,
,
P(η=2)=P(A2)= ![]() ,
,
P(η=3)=P(A3)= ![]() ,
,
∴P(η=1)=1﹣ ![]() =
= ![]() ,
,
∴隨機變量η的分布列為:
η | 0 | 1 | 2 | 3 |
P |
|
|
|
|
Eη= ![]() =
= ![]()
【解析】(1)記“記網民購買i種商品”為事件Ai , i=2,3,分別求出P(A3)和P(A2),由此能求出該網民至少購買2種商品的概率.(2)隨機變量η的可能取值為0,1,2,3,分別求出相應的概率,由此能求出隨機變量η的分布列和Eη.


科目:高中數學 來源: 題型:
【題目】在棱長為1的正方體ABCD﹣A1B1C1D1中,M和N分別為A1B1和BB1的中點,那么直線AM與CN所成角的余弦值是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下表提供了某廠節能降耗技術改進后生產甲產品過程中記錄的產量x(噸)與相應的生產能耗y(噸標準煤)的幾組對照數據.
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
(1)請根據上表提供的數據,用最小二乘法求出y關于x的回歸方程 ![]() ;
;
(2)已知該廠技改前100噸甲產品的生產能耗為90噸標準煤.試根據(1)求出的回歸方程,預測生產100噸甲產品的生產能耗比技改前降低多少噸標準煤?
(參考數值:3×2.5+4×3+5×4+6×4.5=66.5)計算回歸系數 ![]() ,
, ![]() .公式為
.公式為  .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】直三棱柱ABC﹣A1B1C1中,AB⊥AC,AB=2,AC=4,AA1=2, ![]() =λ
=λ ![]() .
. 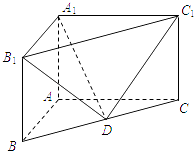
(1)若λ=1,求直線DB1與平面A1C1D所成角的正弦值;
(2)若二面角B1﹣A1C1﹣D的大小為60°,求實數λ的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖, ![]() 是橢圓
是橢圓![]() 的右焦點,
的右焦點, ![]() 是坐標原點,
是坐標原點, ![]() ,過
,過![]() 作
作![]() 的垂線交橢圓于
的垂線交橢圓于![]() ,
, ![]() 兩點,
兩點, ![]() 的面積為
的面積為![]() .
.

(1)求該橢圓的標準方程;
(2)若直線![]() 與上下半橢圓分別交于點
與上下半橢圓分別交于點![]() 、
、![]() ,與
,與![]() 軸交于點
軸交于點![]() ,且
,且![]() ,求
,求![]() 的面積取得最大值時直線
的面積取得最大值時直線![]() 的方程.
的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com