【題目】如圖，在正方體
中，若
是線段
上的動點，則下列結(jié)論不正確的是（ ）
A. 三棱錐
的正視圖面積是定值
B. 異面直線
所成的角可為
C. 三棱錐
的體積大小與點在線段的位置有關(guān)
D. 直線
與平面
所成的角可為
科目：高中數(shù)學 來源： 題型：
【題目】如圖，2012年春節(jié)，攝影愛好者
在某公園
處，發(fā)現(xiàn)正前方
處有一立柱，測得立柱頂端
的仰角和立柱底部
的俯角均為
，設(shè)
的眼睛距地面的距離
米.
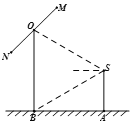
（1）求攝影者到立柱的水平距離和立柱的高度；
（2）立柱的頂端有一長2米的彩桿
繞其中點
在
與立柱所在的平面內(nèi)旋轉(zhuǎn)．攝影者有一視角范圍為
的鏡頭，在彩桿轉(zhuǎn)動的任意時刻，攝影者是否都可以將彩桿全部攝入畫面？說明理由．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)
.
（1）求
在
上的單調(diào)區(qū)間；
（2）當
時，求不等式
的解集；
（3）當
時，設(shè)函數(shù)
，求證：不等式
在定義域上恒成立.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】某企業(yè)生產(chǎn)甲、乙兩種產(chǎn)品．已知生產(chǎn)每噸甲產(chǎn)品要用A原料3噸、B原料2噸；生產(chǎn)每噸乙產(chǎn)品要用A原料1噸、B原料3噸．銷售每噸甲產(chǎn)品可獲得利潤5萬元、每噸乙產(chǎn)品可獲得利潤3萬元．該企業(yè)在一個生產(chǎn)周期內(nèi)消耗A原料不超過13噸、B原料不超過18噸，那么該企業(yè)可獲得最大利潤是（ ）
A.12萬元
B.20萬元
C.25萬元
D.27萬元
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知集合M={x|3+2x﹣x2＞0}，N={x|x＞a}，若MN，則實數(shù)a的取值范圍是（ ）
A.[3，+∞）
B.（3，+∞）
C.（﹣∞，﹣1]
D.（﹣∞，﹣1）
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】目前，學案導(dǎo)學模式已經(jīng)成為教學中不可或缺的一部分，為了了解學案的合理使用是否對學生的期末復(fù)習有著重要的影響，我校隨機抽取100名學生，對學習成績和學案使用程度進行了調(diào)查，統(tǒng)計數(shù)據(jù)如表所示：
已知隨機抽查這100名學生中的一名學生，抽到善于使用學案的學生概率是0.6．
參考公式：
，其中 
．
（1）請將上表補充完整（不用寫計算過程）；
（2）試運用獨立性檢驗的思想方法有多大的把握認為學生的學習成績與對待學案的使用態(tài)度有關(guān)?
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】在數(shù)列{an}中，已知a1= 
，an+1= an﹣ 
，n∈N* ， 設(shè)Sn為{an}的前n項和．
（1）求證：數(shù)列{3nan}是等差數(shù)列；
（2）求Sn；
（3）是否存在正整數(shù)p，q，r（p＜q＜r），使Sp ， Sq ， Sr成等差數(shù)列？若存在，求出p，q，r的值；若不存在，說明理由．
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
