
【題目】已知函數(shù)![]() .
.
(1)討論函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(2)當(dāng)函數(shù)![]() 有兩個(gè)零點(diǎn),求實(shí)數(shù)
有兩個(gè)零點(diǎn),求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
【答案】(1)答案見(jiàn)解析;(2)![]() .
.
【解析】分析:(1)先求導(dǎo),再對(duì)a分類(lèi)討論,求函數(shù)的單調(diào)區(qū)間. (2)對(duì)a分類(lèi)討論,作出函數(shù)的圖像,分析出函數(shù)f(x)有兩個(gè)零點(diǎn)所滿足的條件,從而求出a的取值范圍.
詳解:(1)由題意得![]()
①當(dāng)![]() 時(shí),令
時(shí),令![]() ,則
,則![]() ;
;
令![]() ,則
,則![]() ,
,
∴![]() 在
在![]() 上單調(diào)遞減,在
上單調(diào)遞減,在![]() 上單調(diào)遞增;
上單調(diào)遞增;
②當(dāng)![]() 時(shí),令
時(shí),令![]() ,則
,則![]() 或
或![]() ,
,
(ⅰ)當(dāng)![]() 時(shí),令
時(shí),令![]() ,則
,則![]() 或
或![]() ;
;
令![]() ,則
,則![]() ,
,
∴![]() 在
在![]() 和
和![]() 上單調(diào)遞增,在
上單調(diào)遞增,在![]() 上單調(diào)遞減;
上單調(diào)遞減;
(ⅱ)當(dāng)![]() 時(shí),
時(shí),![]() ,
,
∴![]() 在
在![]() 上單調(diào)遞增;
上單調(diào)遞增;
(ⅲ)當(dāng)![]() 時(shí),令
時(shí),令![]() ,則
,則![]() 或
或![]() ;
;
令![]() ,則
,則![]() ,
,
∴![]() 在
在![]() 和
和![]() 上單調(diào)遞增,在
上單調(diào)遞增,在![]() 上單調(diào)遞減;
上單調(diào)遞減;
(2)由(1)得當(dāng)![]() 時(shí),
時(shí),![]() 在
在![]() 和
和![]() 上單調(diào)遞增,在
上單調(diào)遞增,在![]() 上單調(diào)遞減,
上單調(diào)遞減,
∴![]() 在
在![]() 處取得極大值
處取得極大值![]() ,
,
∵![]() ,
,
∴此時(shí)不符合題意;
當(dāng)![]() 時(shí),
時(shí),![]() 在
在![]() 上單調(diào)遞增,
上單調(diào)遞增,
∴此時(shí)不符合題意;
當(dāng)![]() 時(shí),
時(shí),![]() 在
在![]() 和
和![]() 上單調(diào)遞增,在
上單調(diào)遞增,在![]() 上單調(diào)遞減;
上單調(diào)遞減;
∴![]() 的
的![]() 處取得極大值
處取得極大值![]() ,
,
∵![]() ,
,
∴此時(shí)不符合題意;
當(dāng)![]() 時(shí),
時(shí),![]() 在
在![]() 上單調(diào)遞減,在
上單調(diào)遞減,在![]() 上單調(diào)遞增,
上單調(diào)遞增,
∵![]() ,
,![]() ,
,
∴![]() 在
在![]() 上有一個(gè)零點(diǎn),
上有一個(gè)零點(diǎn),
(ⅰ)當(dāng)![]() 時(shí),令
時(shí),令![]() ,當(dāng)
,當(dāng)![]() 時(shí),
時(shí),
∵![]() ,
,
∴![]() 在
在![]() 上有一個(gè)零點(diǎn),
上有一個(gè)零點(diǎn),
∴此時(shí)符合題意;
(ⅱ)當(dāng)![]() 時(shí),當(dāng)
時(shí),當(dāng)![]() 時(shí),
時(shí),![]() ,
,
∴![]() 在
在![]() 上沒(méi)有零點(diǎn),此時(shí)不符合題意;
上沒(méi)有零點(diǎn),此時(shí)不符合題意;
綜上所述,實(shí)數(shù)![]() 的取值范圍為
的取值范圍為![]() .
.


 閱讀快車(chē)系列答案
閱讀快車(chē)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某基地蔬菜大棚采用水培、無(wú)土栽培方式種植各類(lèi)蔬菜.過(guò)去50周的資料顯示,該地周光照量![]() (小時(shí))都在30小時(shí)以上,其中不足50小時(shí)的周數(shù)有5周,不低于50小時(shí)且不超過(guò)70小時(shí)的周數(shù)有35周,超過(guò)70小時(shí)的周數(shù)有10周.根據(jù)統(tǒng)計(jì),該基地的西紅柿增加量
(小時(shí))都在30小時(shí)以上,其中不足50小時(shí)的周數(shù)有5周,不低于50小時(shí)且不超過(guò)70小時(shí)的周數(shù)有35周,超過(guò)70小時(shí)的周數(shù)有10周.根據(jù)統(tǒng)計(jì),該基地的西紅柿增加量![]() (百斤)與使用某種液體肥料
(百斤)與使用某種液體肥料![]() (千克)之間對(duì)應(yīng)數(shù)據(jù)為如圖所示的折線圖.
(千克)之間對(duì)應(yīng)數(shù)據(jù)為如圖所示的折線圖.

(1)依據(jù)數(shù)據(jù)的折線圖,是否可用線性回歸模型擬合![]() 與
與![]() 的關(guān)系?請(qǐng)計(jì)算相關(guān)系數(shù)
的關(guān)系?請(qǐng)計(jì)算相關(guān)系數(shù)![]() 并加以說(shuō)明(精確到0.01);(若
并加以說(shuō)明(精確到0.01);(若![]() ,則線性相關(guān)程度很高,可用線性回歸模型擬合)
,則線性相關(guān)程度很高,可用線性回歸模型擬合)
(2)蔬菜大棚對(duì)光照要求較大,某光照控制儀商家為該基地提供了部分光照控制儀,但每周光照控制儀最多可運(yùn)行臺(tái)數(shù)受周光照量![]() 限制,并有如表關(guān)系:
限制,并有如表關(guān)系:

若某臺(tái)光照控制儀運(yùn)行,則該臺(tái)光照控制儀周利潤(rùn)為3000元;若某臺(tái)光照控制儀未運(yùn)行,則該臺(tái)光照控制儀周虧損1000元.以過(guò)去50周的周光照量的頻率作為周光照量發(fā)生的概率,商家欲使周總利潤(rùn)的均值達(dá)到最大,應(yīng)安裝光照控制儀多少臺(tái)?
附:相關(guān)系數(shù)公式 ,參考數(shù)據(jù)
,參考數(shù)據(jù)![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)函數(shù)![]() 的定義域?yàn)?/span>
的定義域?yàn)?/span>![]() ,若存在閉區(qū)間
,若存在閉區(qū)間![]()
![]() ,使得
,使得![]() 函數(shù)滿足:(1)
函數(shù)滿足:(1)![]() 在
在![]() 上是單調(diào)函數(shù);(2)
上是單調(diào)函數(shù);(2)![]() 在
在![]() 上的值域是
上的值域是![]() ,則稱(chēng)區(qū)間
,則稱(chēng)區(qū)間![]() 是函數(shù)
是函數(shù)![]() 的“和諧區(qū)間”,下列結(jié)論錯(cuò)誤的是( )
的“和諧區(qū)間”,下列結(jié)論錯(cuò)誤的是( )
A.函數(shù)![]() 存在“和諧區(qū)間”
存在“和諧區(qū)間”
B.函數(shù)![]() 不存在“和諧區(qū)間”
不存在“和諧區(qū)間”
C.函數(shù)![]()
![]() 存在“和諧區(qū)間”
存在“和諧區(qū)間”
D.函數(shù)![]() (
(![]() ,
,![]() )不存在“和諧區(qū)間”
)不存在“和諧區(qū)間”
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】歷史數(shù)據(jù)顯示:某城市在每年的3月11日—3月15日的每天平均氣溫只可能是-5℃,-6℃,-7℃,-8℃中的一個(gè),且等可能出現(xiàn).
(Ⅰ)求該城市在3月11日—3月15日這5天中,恰好出現(xiàn)兩次-5℃,一次-8℃的概率;
(Ⅱ)若該城市的某熱飲店,隨平均氣溫的變化所售熱飲杯數(shù)如下表
平均氣溫t | -5℃ | -6℃ | -7℃ | -8℃ |
所售杯數(shù)y | 19 | 22 | 24 | 27 |
根據(jù)以上數(shù)據(jù),求![]() 關(guān)于
關(guān)于![]() 的線性回歸直線方程.
的線性回歸直線方程.
(參考公式: ,
,![]() )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某廠生產(chǎn)某產(chǎn)品的年固定成本為250萬(wàn)元,每生產(chǎn)![]() 千件,需另投入成本
千件,需另投入成本![]() (萬(wàn)元),若年產(chǎn)量不足
(萬(wàn)元),若年產(chǎn)量不足![]() 千件,
千件, ![]() 的圖像是如圖的拋物線,此時(shí)
的圖像是如圖的拋物線,此時(shí)![]() 的解集為
的解集為![]() ,且
,且![]() 的最小值是
的最小值是![]() ,若年產(chǎn)量不小于
,若年產(chǎn)量不小于![]() 千件,
千件, ![]() ,每千件商品售價(jià)為50萬(wàn)元,通過(guò)市場(chǎng)分析,該廠生產(chǎn)的商品能全部售完;
,每千件商品售價(jià)為50萬(wàn)元,通過(guò)市場(chǎng)分析,該廠生產(chǎn)的商品能全部售完;
(1)寫(xiě)出年利潤(rùn)![]() (萬(wàn)元)關(guān)于年產(chǎn)量
(萬(wàn)元)關(guān)于年產(chǎn)量![]() (千件)的函數(shù)解析式;
(千件)的函數(shù)解析式;
(2)年產(chǎn)量為多少千件時(shí),該廠在這一商品的生產(chǎn)中所獲利潤(rùn)最大?

查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】根據(jù)統(tǒng)計(jì),某市騎行過(guò)共享單車(chē)的人數(shù)約占全市的80%,為確定單車(chē)的投放數(shù)量以及對(duì)同年齡的車(chē)型配比,需要對(duì)該市市民每月騎行單車(chē)的次數(shù)進(jìn)行統(tǒng)計(jì),如表所示是對(duì)該市隨機(jī)抽取100位市民的調(diào)查結(jié)果,每月騎行次數(shù)不超過(guò)20次稱(chēng)“不經(jīng)常騎行”,超過(guò)20次稱(chēng)“經(jīng)常騎行”.
經(jīng)常騎行 | 不經(jīng)常騎行 | 合計(jì) | |
年齡不低于40歲 | 15 | 25 | 40 |
年齡低于40歲 | 35 | 25 | 60 |
合計(jì) | 50 | 50 | 100 |
(1)是否有95%的把握認(rèn)為騎行單車(chē)次數(shù)與年齡有關(guān)?
(2)以樣本的頻率為概率
①現(xiàn)從該市市民中隨機(jī)抽取1人,求該人為“經(jīng)常騎行”的概率
②已知該市人口約為600萬(wàn),忽略把經(jīng)常騎行人數(shù)的騎行次數(shù),統(tǒng)計(jì)得經(jīng)常騎行人群每人每月騎行次數(shù)的平均值為45次(每月按30天計(jì)算),若每輛單車(chē)每天被騎行(15次左右,可達(dá)到既緩解交通壓力又減少了胡亂放置的目的,則該市配置單車(chē)的數(shù)量應(yīng)為多少?
附參考公式及數(shù)據(jù)![]()
| 0.10 | 0.050 | 0.010 |
| 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】支付寶和微信支付是目前市場(chǎng)占有率較高的支付方式,某第三方調(diào)研機(jī)構(gòu)對(duì)使用這兩種支付方式的人數(shù)作了對(duì)比.從全國(guó)隨機(jī)抽取了100個(gè)地區(qū)作為研究樣本,計(jì)算了各個(gè)地區(qū)樣本的使用人數(shù),其頻率分布直方圖如圖.
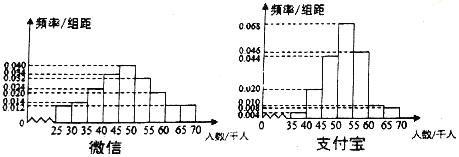
(1)記A表示事件“微信支付人數(shù)低于50千人”,估計(jì)A的概率;
(2)填寫(xiě)下面列聯(lián)表,并根據(jù)列聯(lián)表判斷是否有99%的把握認(rèn)為支付人數(shù)與支付方式有關(guān);
支付人數(shù)<50千人 | 支付人數(shù)≥50千人 | 總計(jì) | |
微信支付 | |||
支付寶支付 | |||
總計(jì) |
(3)根據(jù)支付人數(shù)的頻率分布直方圖,對(duì)兩種支付方式的優(yōu)劣進(jìn)行比較.
附:
P(K2≥K) | 0.050 | 0.010 | 0.001 |
K | 3.841 | 6.635 | 10.828 |
K2=![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() 的定義域?yàn)?/span>
的定義域?yàn)?/span>![]() ,
,![]() 的定義域?yàn)?/span>
的定義域?yàn)?/span>![]() .
.
(1)求出集合![]() ;
;
(2)求![]() ;
;
(3)若![]() ,且
,且![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖: PA⊥平面ABC,∠ACB=90°且PA=AC=BC=![]() ,則異面直線PB與AC所成角的正切值等于________.
,則異面直線PB與AC所成角的正切值等于________.

查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com