【題目】從某小學隨機抽取100名學生，將他們的身高（單位：厘米）數據繪制成頻率分布直方圖（如圖），若要從身高在[120，130），[130，140），[140，150]三組內的學生中，用分層抽樣的方法選取18人參加一項活動，則從身高在[120，130）內的學生中選取的人數應為（ ）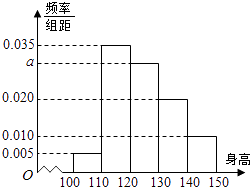 
A.10
B.9
C.8
D.7
【答案】B
【解析】解：由頻率分布直方圖得：
10a=1﹣（0.005+0.035+0.020+0.010）×10=0.3，
解得a=0.03．
∴身高在[120，130），[130，140），[140，150]三組內的學生人數分別為：
0.03×10×100=30，0.02×10×100=20，0.01×10×100=10，
∴從身高在[120，130），[130，140），[140，150]三組內的學生中，
用分層抽樣的方法選取18人參加一項活動，
則從身高在[120，130）內的學生中選取的人數應為：30× 
=9（人）．
故選：B．
【考點精析】掌握頻率分布直方圖是解答本題的根本，需要知道頻率分布表和頻率分布直方圖，是對相同數據的兩種不同表達方式.用緊湊的表格改變數據的排列方式和構成形式，可展示數據的分布情況.通過作圖既可以從數據中提取信息，又可以利用圖形傳遞信息．
科目：高中數學 來源： 題型：
【題目】設集合M={x|0≤x≤2}，N={y|0≤y≤2}，從M到N有四種對應如圖所示：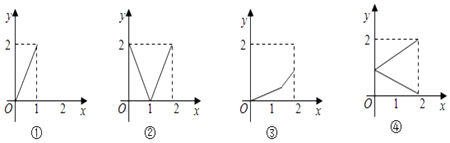 
其中能表示為M到N的映射關系的有（請填寫符合條件的序號）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓E：
=1（a＞b＞0）的焦距為2
， 且該橢圓經過點(,
)．
（Ⅰ）求橢圓E的方程；
（Ⅱ）經過點P（﹣2，0）分別作斜率為k1 ， k2的兩條直線，兩直線分別與橢圓E交于M，N兩點，當直線MN與y軸垂直時，求k1k2的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知等差數列{an}的前n項的和記為Sn ． 如果a4=﹣12，a8=﹣4．
（1）求數列{an}的通項公式；
（2）求Sn的最小值及其相應的n的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，已知橢圓
： 
的離心率
，短軸右端點為
， 
為線段
的中點.
(Ⅰ) 求橢圓
的方程；
(Ⅱ)過點
任作一條直線與橢圓
相交于兩點
，試探究在
軸上是否存在定點
，使得
，若存在，求出點
的坐標；若不存在，說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=2sinωxcosωx+cos2ωx（ω＞0），且f（x）的最小正周期為π
（1）求函數f（x）的單調增區間；
（2）若f（ 
﹣ 
）= 
，f（ 
﹣ ）= 
，且α、β∈（﹣ 
），求cos（α+β）的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某車間為了規定工時定額，需要確定加工某零件所花費的時間，為此做了四次實驗，得到的數據如表：
零件的個數x（個） | 2 | 3 | 4 | 5 |
加工的時間y（小時） | 2.5 | 3 | 4 | 4.5 |
（1）在給定的坐標系中畫出表中數據的散點圖；
（2）求出y關于x的線性回歸方程y= 
x+ 
，并在坐標系中畫出回歸直線；
（3）試預測加工6個零件需要多少時間？
（注： = 
， = 
﹣ 
）
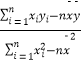查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設命題p：實數x滿足x2﹣4ax+3a2＜0，其中a＞0，命題q：實數x滿足
．
（Ⅰ）若a=1，且p∧q為真，求實數x的取值范圍；
（Ⅱ）若￢p是￢q的充分不必要條件，求實數a的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
