
【題目】已知橢圓E:![]() =1(a>b>0)的焦距為2
=1(a>b>0)的焦距為2![]() , 且該橢圓經過點(
, 且該橢圓經過點(![]() ,
,![]() ).
).
(Ⅰ)求橢圓E的方程;
(Ⅱ)經過點P(﹣2,0)分別作斜率為k1 , k2的兩條直線,兩直線分別與橢圓E交于M,N兩點,當直線MN與y軸垂直時,求k1k2的值.
【答案】解:(Ⅰ)由題意得,2c=2![]() ,
,![]() =1;
=1;
解得,a2=4,b2=1;
故橢圓E的方程為![]() +y2=1;
+y2=1;
(Ⅱ)由題意知,當k1=0時,M點的縱坐標為0,
直線MN與y軸垂直,
則點N的縱坐標為0,
故k2=k1=0,這與k2≠k1矛盾.
當k1≠0時,直線PM:y=k1(x+2);
由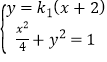 得,
得,
(![]() +4)y2﹣
+4)y2﹣![]() =0;
=0;
解得,yM=![]() ;
;
∴M(![]() ,
,![]() ),
),
同理N(![]() ,
,![]() ),
),
由直線MN與y軸垂直,則![]() =
=![]() ;
;
∴(k2﹣k1)(4k2k1﹣1)=0,
∴k2k1=![]() .
.
【解析】(Ⅰ)由題意得,2c=2![]() ,
, ![]() =1;從而求橢圓E的方程;
=1;從而求橢圓E的方程;
(Ⅱ)由題意知,當k1=0時,M點的縱坐標為0,點N的縱坐標為0,故不成立;當k1≠0時,直線PM:y=k1(x+2);聯立方程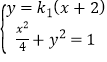 得(
得(![]() +4)y2﹣
+4)y2﹣![]() =0;從而解得yM=
=0;從而解得yM=![]() ;可得M(
;可得M(![]() ,
, ![]() ),N(
),N(![]() ,
, ![]() );從而可得(k2﹣k1)(4k2k1﹣1)=0,從而解得.
);從而可得(k2﹣k1)(4k2k1﹣1)=0,從而解得.
【考點精析】解答此題的關鍵在于理解橢圓的標準方程的相關知識,掌握橢圓標準方程焦點在x軸:![]() ,焦點在y軸:
,焦點在y軸:![]() .
.


科目:高中數學 來源: 題型:
【題目】設點![]() ,直線
,直線![]() ,點
,點![]() 在直線
在直線![]() 上移動,
上移動, ![]() 是線段
是線段![]() 與
與![]() 軸的交點,
軸的交點, ![]() .
.
(Ⅰ) 求動點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(Ⅱ)直線![]() 與
與![]() 軸相交于點
軸相交于點![]() ,過
,過![]() 的直線
的直線![]() 交軌跡
交軌跡![]() 于
于![]() 兩點,
兩點,
試探究點![]() 與以
與以![]() 為直徑的圓的位置關系,并加以說明.
為直徑的圓的位置關系,并加以說明.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,M、N是焦點為F的拋物線y2=2px(p>0)上兩個不同的點,且線段MN中點A的橫坐標為4-![]() ,
,
(1)求|MF|+|NF|的值;
(2)若p=2,直線MN與x軸交于點B點,求點B橫坐標的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,EP交圓于E,C兩點,PD切圓于D,G為CE上一點且PG=PD,連結DG并延長交圓于點A,作弦AB垂直EP,垂足為F.
(Ⅰ)求證:AB為圓的直徑;
(Ⅱ)若AC=BD,求證:AB=ED.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,角A、B、C所對的邊分別為a,b,c,已知cos2C= ![]() .
.
(1)求sinC的值;
(2)當a=2,2sinA=sinC時,求b及c的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從某小學隨機抽取100名學生,將他們的身高(單位:厘米)數據繪制成頻率分布直方圖(如圖),若要從身高在[120,130),[130,140),[140,150]三組內的學生中,用分層抽樣的方法選取18人參加一項活動,則從身高在[120,130)內的學生中選取的人數應為( ) 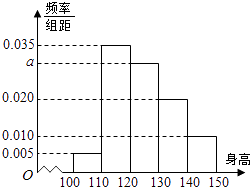
A.10
B.9
C.8
D.7
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com