
【題目】如圖,某市郊外景區(qū)內(nèi)一條筆直的公路![]() 經(jīng)過三個景點
經(jīng)過三個景點![]() 、
、![]() 、
、![]() ,景區(qū)管委會又開發(fā)了風景優(yōu)美的景點
,景區(qū)管委會又開發(fā)了風景優(yōu)美的景點![]() ,經(jīng)測量景點
,經(jīng)測量景點![]() 位于景點
位于景點![]() 的北偏東
的北偏東![]() 方向
方向![]() 處,位于景點
處,位于景點![]() 的正北方向,還位于景點
的正北方向,還位于景點![]() 的北偏西
的北偏西![]() 方向上,已知
方向上,已知![]() .
.
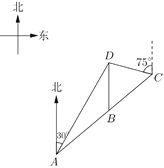
(1)景區(qū)管委會準備由景點![]() 向景點
向景點![]() 修建一條筆直的公路,不考慮其他因素,求出這條公路的長;(結果精確到
修建一條筆直的公路,不考慮其他因素,求出這條公路的長;(結果精確到![]() )
)
(2)求景點![]() 與景點
與景點![]() 之間的距離.(結果精確到
之間的距離.(結果精確到![]() )
)
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
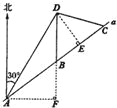
(1)過點D作DE⊥AC于點E,過點A作AF⊥DB,交DB的延長線于點F,求DE的問題就可以轉化為求∠DBE的度數(shù)或三角函數(shù)值的問題.
(2)Rt△DCE中根據(jù)三角函數(shù)就可以求出CD的長.
(1)如圖,過點D作DE⊥AC于點E,過點A作AF⊥DB,交DB的延長線于點F
在Rt△DAF中,∠ADF=30°,∴AF![]() AD
AD![]() 8=4,∴DF
8=4,∴DF![]() ;
;
在Rt△ABF中,BF![]() 3,∴BD=DF﹣BF=4
3,∴BD=DF﹣BF=4![]() 3
3
sin∠ABF![]() ,在Rt△DBE中,sin∠DBE
,在Rt△DBE中,sin∠DBE![]() ,
,
∵∠ABF=∠DBE,∴sin∠DBE![]() ,
,
∴DE=BDsin∠DBE![]() (4
(4![]() 3)
3)![]() 3.1(km)
3.1(km)
∴景點D向公路a修建的這條公路的長約是3.1km;
(2)由題意可知∠CDB=75°,由(1)可知sin∠DBE![]() 0.8,所以∠DBE=53°,∴∠DCB=180°﹣75°﹣53°=52°
0.8,所以∠DBE=53°,∴∠DCB=180°﹣75°﹣53°=52°
在Rt△DCE中,sin∠DCE![]() ,∴DC
,∴DC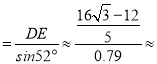 4.0(km)
4.0(km)
∴景點C與景點D之間的距離約為4.0km.


 口算題卡加應用題集訓系列答案
口算題卡加應用題集訓系列答案 綜合自測系列答案
綜合自測系列答案科目:高中數(shù)學 來源: 題型:
【題目】已知雙曲線 C 經(jīng)過點 (2,3),它的漸近線方程為 y = ±![]() .橢圓 C1與雙曲線 C有相同的焦點,橢圓 C1的短軸長與雙曲線 C 的實軸長相等.
.橢圓 C1與雙曲線 C有相同的焦點,橢圓 C1的短軸長與雙曲線 C 的實軸長相等.
(1)求雙曲線 C 和橢圓 C1 的方程;
(2)經(jīng)過橢圓 C1 左焦點 F 的直線 l 與橢圓 C1 交于 A、B 兩點,是否存在定點 D ,使得無論 AB 怎樣運動,都有∠ADF = ∠BDF ?若存在,求出 D 點坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,點
,點 在
在![]() 上.
上.
(1) 求橢圓的方程;
(2) 設![]() 分別是橢圓
分別是橢圓![]() 的上、下焦點,過
的上、下焦點,過![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于不同的兩點
交于不同的兩點![]() ,求
,求![]() 的內(nèi)切圓的半徑的最大值.
的內(nèi)切圓的半徑的最大值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】為了了解居民的家庭收入情況,某社區(qū)組織工作人員從該社區(qū)的居民中隨機抽取了![]() 戶家庭進行問卷調(diào)查,經(jīng)調(diào)查發(fā)現(xiàn),這些家庭的月收人在
戶家庭進行問卷調(diào)查,經(jīng)調(diào)查發(fā)現(xiàn),這些家庭的月收人在![]() 元到
元到![]() 元之間,根據(jù)統(tǒng)計數(shù)據(jù)作出:
元之間,根據(jù)統(tǒng)計數(shù)據(jù)作出:
(1)經(jīng)統(tǒng)計發(fā)現(xiàn),該社區(qū)居民的家庭月收人![]() (單位:百元)近似地服從正態(tài)分布
(單位:百元)近似地服從正態(tài)分布![]() ,其中
,其中![]() 近似為樣本平均數(shù).若
近似為樣本平均數(shù).若![]() 落在區(qū)間
落在區(qū)間![]() 的左側,則可認為該家庭屬“收入較低家庭" ,社區(qū)將聯(lián)系該家庭,咨詢收入過低的原因,并采取相應措施為該家庭提供創(chuàng)收途徑.若該社區(qū)
的左側,則可認為該家庭屬“收入較低家庭" ,社區(qū)將聯(lián)系該家庭,咨詢收入過低的原因,并采取相應措施為該家庭提供創(chuàng)收途徑.若該社區(qū)![]() 家庭月收入為
家庭月收入為![]() 元,試判斷
元,試判斷![]() 家庭是否屬于“收人較低家庭”,并說明原因;
家庭是否屬于“收人較低家庭”,并說明原因;
(2)將樣本的頻率視為總體的概率
①從該社區(qū)所有家庭中隨機抽取![]() 戶家庭,若這
戶家庭,若這![]() 戶家庭月收人均低于
戶家庭月收人均低于![]() 元的概率不小于
元的概率不小于![]() ,求
,求![]() 的最大值;
的最大值;
②在①的條件下,某生活超市贊助了該社區(qū)的這次調(diào)查活動,并為這次參與調(diào)在的家庭制定了贈送購物卡的活動,贈送方式為:家庭月收入低于![]() 的獲贈兩次隨機購物卡,家庭月收入不低于
的獲贈兩次隨機購物卡,家庭月收入不低于![]() 的獲贈一次隨機購物卡;每次贈送的購物卡金額及對應的概率分別為:
的獲贈一次隨機購物卡;每次贈送的購物卡金額及對應的概率分別為:
贈送購物卡金額(單位:元) |
|
|
|
概率 |
|
|
|
則![]() 家庭預期獲得的購物卡金額為多少元?(結果保留整數(shù))
家庭預期獲得的購物卡金額為多少元?(結果保留整數(shù))

查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某中學為豐富教職工生活,在元旦期間舉辦趣味投籃比賽,設置A,B兩個投籃位置,在A點投中一球得1分,在B點投中一球得2分,規(guī)則是:每人按先A后B的順序各投籃一次(計為投籃兩次),教師甲在A點和B點投中的概率分別為![]() 和
和![]() ,且在A,B兩點投中與否相互獨立.
,且在A,B兩點投中與否相互獨立.
(1)若教師甲投籃兩次,求教師甲投籃得分0分的概率
(2)若教師乙與教師甲在A,B投中的概率相同,兩人按規(guī)則投籃兩次,求甲得分比乙高的概率.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在平面直角坐標系中![]() ,以原點
,以原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸,建立極坐標系,直線
軸正半軸為極軸,建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() ,曲線
,曲線![]() 的參數(shù)方程為:
的參數(shù)方程為: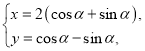 (
(![]() 為參數(shù)),
為參數(shù)),![]() ,
,![]() 為直線
為直線![]() 上距離為
上距離為![]() 的兩動點,點
的兩動點,點![]() 為曲線
為曲線![]() 上的動點且不在直線
上的動點且不在直線![]() 上.
上.
(1)求曲線![]() 的普通方程及直線
的普通方程及直線![]() 的直角坐標方程.
的直角坐標方程.
(2)求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】函數(shù)![]() ,其中
,其中![]() .
.
(1)討論![]() 的奇偶性;
的奇偶性;
(2)![]() 時,求證:
時,求證:![]() 的最小正周期是
的最小正周期是![]() ;
;
(3)![]() ,當函數(shù)
,當函數(shù)![]() 的圖像與
的圖像與![]() 的圖像有交點時,求滿足條件的
的圖像有交點時,求滿足條件的![]() 的個數(shù),說明理由.
的個數(shù),說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,某污水處理廠要在一個矩形污水處理池(ABCD)的池底水平鋪設污水凈化管道(管道構成Rt△FHE,H是直角項點)來處理污水.管道越長,污水凈化效果越好.設計要求管道的接口H是AB的中點,E,F(xiàn)分別落在線段BC,AD上.已知AB=20米,AD=![]() 米,記∠BHE=
米,記∠BHE=![]() .
.

(1)試將污水凈化管道的長度L表示為![]() 的函數(shù),并寫出定義域;
的函數(shù),并寫出定義域;
(2)當![]() 取何值時,污水凈化效果最好?并求出此時管道的長度L.
取何值時,污水凈化效果最好?并求出此時管道的長度L.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() ;
;
(1)當![]() 時,若
時,若![]() ,求
,求![]() 的取值范圍;
的取值范圍;
(2)若定義在![]() 上奇函數(shù)
上奇函數(shù)![]() 滿足
滿足![]() ,且當
,且當![]() 時,
時, ![]() ,
,
求![]() 在
在![]() 上的反函數(shù)
上的反函數(shù)![]() ;
;
(3)對于(2)中的![]() ,若關于
,若關于![]() 的不等式
的不等式 在
在![]() 上恒成立,求實
上恒成立,求實
數(shù)![]() 的取值范圍;
的取值范圍;
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com