
���}Ŀ����֪����(sh��)![]() ��
�� ![]() ��������
��������![]() ��
�� ![]() ����Ȼ��(du��)��(sh��)�ĵה�(sh��)��
����Ȼ��(du��)��(sh��)�ĵה�(sh��)�� ![]() ������.
������.
��1����![]() ����
����![]() ��(du��)�����
��(du��)�����![]() ���������(sh��)��(sh��)
���������(sh��)��(sh��)![]() ��ֵ��
��ֵ��
��2���ڣ�1���ėl���£��O(sh��)![]() ������(sh��)���Ҍ�(du��)������������(sh��)
������(sh��)���Ҍ�(du��)������������(sh��)![]() ��
�� ![]() ����
����![]() ����Сֵ.
����Сֵ.
���𰸡���1��![]() ����2��
����2��![]() .
.
��������ԇ�}��������1����![]() ��(du��)�����
��(du��)�����![]() ���������
���������![]() �����Ì�(d��o)��(sh��)ӑՓ����(sh��)�Ć��{(di��o)�ԣ������Сֵ�����ɵõ���(sh��)��(sh��)
�����Ì�(d��o)��(sh��)ӑՓ����(sh��)�Ć��{(di��o)�ԣ������Сֵ�����ɵõ���(sh��)��(sh��)![]() ��ֵ����2���ɣ�1��֪
��ֵ����2���ɣ�1��֪![]() ����
����![]() ��
��
��![]() ��
��![]() ��
�� ![]() ���t
���t![]() ������
������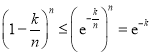 ����
����![]() ����ͺ����÷ſs���ɵ�
����ͺ����÷ſs���ɵ�![]() ���Ķ��ɵ�
���Ķ��ɵ�![]() ����Сֵ.
����Сֵ.
����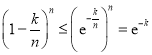 ��.
��.
ԇ�}��������1����?y��n)?/span>![]()
����![]() ��
��
��![]() ��(du��)�����
��(du��)�����![]() ���������
���������![]() ��
��
��![]() ��
��
��i����(d��ng)![]() �r(sh��)��
�r(sh��)�� ![]() ��
�� ![]() ���{(di��o)�f���^(q��)�g��
���{(di��o)�f���^(q��)�g��![]() ��
��
����![]() �r(sh��)��
�r(sh��)�� ![]() ��
��
���Բ��M���}��.
(ii)��(d��ng)![]() �r(sh��)����
�r(sh��)����![]() ����
����![]()
![]() �r(sh��)��
�r(sh��)�� ![]() ��
�� ![]() �r(sh��)��
�r(sh��)�� ![]() ��
��
����![]() �څ^(q��)�g
�څ^(q��)�g![]() �φ��{(di��o)�f�p���څ^(q��)�g
�φ��{(di��o)�f�p���څ^(q��)�g![]() �φ��{(di��o)�f����
�φ��{(di��o)�f����
����![]() ����Сֵ��
����Сֵ��![]() .
.
�O(sh��)![]() ������
������![]() ����
����
��?y��n)?/span>![]()
��![]() ��
��![]() ��
��
����![]() �څ^(q��)�g
�څ^(q��)�g![]() �φ��{(di��o)�f�����څ^(q��)�g
�φ��{(di��o)�f�����څ^(q��)�g![]() �φ��{(di��o)�f�p��
�φ��{(di��o)�f�p��
����![]() ����
����
���٢���![]() ���t
���t![]() .
.
��2���ɣ�1��֪![]() ����
����![]() ��
��
��![]() ��
��![]() ��
�� ![]() ���t
���t![]() ��
��
���� ��
��
����![]()
![]() ��
��
����![]() ��
��
��![]() ��
��
����![]() ����Сֵ��
����Сֵ��![]() .
.


 ��x��܇ϵ�д�
��x��܇ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����ƽ��ֱ������(bi��o)ϵ![]() �У�����
�У�����![]() �ą���(sh��)���̞�
�ą���(sh��)���̞�![]() ��
��![]() �酢��(sh��)��������
�酢��(sh��)��������![]() �ą���(sh��)���̞�
�ą���(sh��)���̞�![]() ��
��![]() �酢��(sh��)����������(bi��o)ԭ�c(di��n)
�酢��(sh��)����������(bi��o)ԭ�c(di��n)![]() ��O�c(di��n)��
��O�c(di��n)��![]() �S�������S��O�S�����O����(bi��o)ϵ.
�S�������S��O�S�����O����(bi��o)ϵ.
��1��������![]() ������
������![]() �ĘO����(bi��o)���̣�
�ĘO����(bi��o)���̣�
��2����֪�侀![]() ��
��![]() �������侀
�������侀![]() 형r(sh��)ᘷ������D(zhu��n)
형r(sh��)ᘷ������D(zhu��n)![]() �õ�
�õ�![]() ��
��![]() �����侀
�����侀![]() �c����
�c����![]() ���ڃ��c(di��n)���侀
���ڃ��c(di��n)���侀![]() �c����
�c����![]() ����
����![]() ���c(di��n)����
���c(di��n)����![]() �����ֵ.
�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() .
.
��1����(sh��)![]() �ĘOֵ;
�ĘOֵ;
��2����(d��ng)![]() �r(sh��)���C����
�r(sh��)���C����![]() ;
;
��3���O(sh��)����(sh��)![]() �ĈD���cֱ��
�ĈD���cֱ��![]() �ăɂ�(g��)���c(di��n)�քe��
�ăɂ�(g��)���c(di��n)�քe��![]() ��
��![]() ��
��![]() �����c(di��n)�ęM����(bi��o)��
�����c(di��n)�ęM����(bi��o)��![]() ���C����
���C����![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() .
.
��1����![]() ����
����![]() �����c(di��n)��(g��)��(sh��)��
�����c(di��n)��(g��)��(sh��)��
��2����![]() ��
��![]() ���C����
���C����![]() ��
��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D��������![]() �У���(c��)��
����(c��)��![]() ��(c��)��
��(c��)��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() �����c(di��n)��
�����c(di��n)��![]() ����
����![]() �ϣ�
�ϣ�![]() ��
��![]() .
.

��1�����C��![]() ��
��![]() �����c(di��n)��
�����c(di��n)��
��2��������![]() ������ֵ.
������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��ij���a(ch��n)�н鹫˾2017��9��1����ʽ�_�I(y��)���F(xi��n)��(du��)��ÿ��(g��)�µĶ��ַ��ɽ����M(j��n)�нy(t��ng)Ӌ(j��)��![]() ��ʾ�_�I(y��)��
��ʾ�_�I(y��)��![]() ��(g��)�µĶ��ַ��ɽ������õ��y(t��ng)Ӌ(j��)�������£�
��(g��)�µĶ��ַ��ɽ������õ��y(t��ng)Ӌ(j��)�������£�

��1���y(t��ng)Ӌ(j��)�г������P(gu��n)ϵ��(sh��)![]() ������?j��)ɂ�(g��)׃��֮�g�����P(gu��n)ϵ�ď�(qi��ng)��.�y(t��ng)Ӌ(j��)�W(xu��)�J(r��n)�飬��(du��)��׃��
������?j��)ɂ�(g��)׃��֮�g�����P(gu��n)ϵ�ď�(qi��ng)��.�y(t��ng)Ӌ(j��)�W(xu��)�J(r��n)�飬��(du��)��׃��![]() �����
�����![]() ����ô���P(gu��n)�Ժ�(qi��ng)�����
����ô���P(gu��n)�Ժ�(qi��ng)�����![]() ����ô���P(gu��n)��һ�㣻���
����ô���P(gu��n)��һ�㣻���![]() ����ô���P(gu��n)���^��.ͨ�^ɢ�c(di��n)�D�����������þ��Իؚwģ�͔M��
����ô���P(gu��n)���^��.ͨ�^ɢ�c(di��n)�D�����������þ��Իؚwģ�͔M��![]() �c
�c![]() ���P(gu��n)ϵ.Ӌ(j��)��
���P(gu��n)ϵ.Ӌ(j��)��![]() �����P(gu��n)ϵ��(sh��)
�����P(gu��n)ϵ��(sh��)![]() �����ش��Ƿ�����J(r��n)��ɂ�(g��)׃�����к�(qi��ng)�ľ������P(gu��n)�P(gu��n)ϵ��Ӌ(j��)��Y(ji��)�����_��0.01��
�����ش��Ƿ�����J(r��n)��ɂ�(g��)׃�����к�(qi��ng)�ľ������P(gu��n)�P(gu��n)ϵ��Ӌ(j��)��Y(ji��)�����_��0.01��
��2��Ո(q��ng)����(j��)�ϱ��ṩ�Ĕ�(sh��)��(j��)������С���˷����![]() �P(gu��n)��
�P(gu��n)��![]() �ľ��Իؚw����
�ľ��Իؚw����![]() ��Ӌ(j��)��Y(ji��)�����_��0.01�������A(y��)�y(c��)ԓ���a(ch��n)�н鹫˾2018��6�·ݵĶ��ַ��ɽ�����Ӌ(j��)��Y(ji��)����������ȡ����(sh��)��.
��Ӌ(j��)��Y(ji��)�����_��0.01�������A(y��)�y(c��)ԓ���a(ch��n)�н鹫˾2018��6�·ݵĶ��ַ��ɽ�����Ӌ(j��)��Y(ji��)����������ȡ����(sh��)��.
������(sh��)��(j��)��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() .
.
������ʽ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() .
.
��1��ӑՓ![]() �Ć��{(di��o)�ԣ�
�Ć��{(di��o)�ԣ�
��2����![]() �Ѓɂ�(g��)�Oֵ�c(di��n)
�Ѓɂ�(g��)�Oֵ�c(di��n)![]() ���C����
���C����![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���������}:
�ل�(d��ng)�c(di��n)M�������c(di��n)A��B�ľ��x֮�Ȟ鳣��(sh��)![]() �t��(d��ng)�c(di��n)M��܉�E�LjA
�t��(d��ng)�c(di��n)M��܉�E�LjA
�ڙE�A![]() ���x���ʞ�
���x���ʞ�![]() ,�t
,�t![]()
���p����![]() �Ľ��c(di��n)���u�����ľ��x��
�Ľ��c(di��n)���u�����ľ��x��![]()
����֪���タ![]() �σ��c(di��n)
�σ��c(di��n)![]() (
(![]() ������(bi��o)ԭ�c(di��n)),�t
������(bi��o)ԭ�c(di��n)),�t![]()
�������}���_����( )
A.�ڢۢ�B.�٢�
C.�٢�D.�٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��������S���҇�(gu��)�ڽ��������ϵ�Ͷ�벻��Ӵ�,�ƌW(xu��)���g(sh��)�õ�Ѹ�Ͱl(f��)չ,��(gu��)��(n��i)��I(y��)�ć�(gu��)�H��(j��ng)��(zh��ng)���õ��������.���S����(gu��)��(n��i)�Ј�(ch��ng)���ٷž�,��(gu��)��(n��i)�Ќ�(sh��)����I(y��)�����M(j��n)�к��Ⲽ��,�ڶ�݆��I(y��)����������.���������֙C(j��)�ИI(y��),��(gu��)�a(ch��n)Ʒ�������s����(gu��)����^,ijƷ���֙C(j��)��˾һֱĬĬ��չ�����Ј�(ch��ng),�ں���O(sh��)![]() ����(g��)��֧�C(j��)��(g��u),��Ҫ��(gu��)��(n��i)��˾���ɴ���
����(g��)��֧�C(j��)��(g��u),��Ҫ��(gu��)��(n��i)��˾���ɴ���![]() ��
��![]() ��������T��.ԓ��I(y��)���˽��@�ɂ�(g��)���g�ӆT���Ƿ�Ը�ⱻ���ɹ����đB(t��i)��,���ӳ�ӵķ�ʽ��
��������T��.ԓ��I(y��)���˽��@�ɂ�(g��)���g�ӆT���Ƿ�Ը�ⱻ���ɹ����đB(t��i)��,���ӳ�ӵķ�ʽ��![]() ���
���![]() ��ĆT�����S�C(j��)�{(di��o)����
��ĆT�����S�C(j��)�{(di��o)����![]() λ,�õ���(sh��)��(j��)���±���
λ,�õ���(sh��)��(j��)���±���
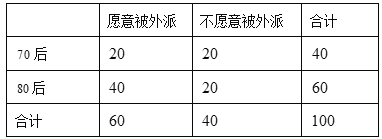
(1)����(j��)�{(di��o)��Ĕ�(sh��)��(j��),�Ƿ���![]() ���ϵİ����J(r��n)�顰�Ƿ�Ը�ⱻ�����c���g���P(gu��n)��,���f�����ɣ�
���ϵİ����J(r��n)�顰�Ƿ�Ը�ⱻ�����c���g���P(gu��n)��,���f�����ɣ�
(2)ԓ��˾�e�Ѕ��^�v�����֧�C(j��)��(g��u)�Ľ����w�(y��n)���(d��ng),�M����![]() �����c�{(di��o)���
�����c�{(di��o)���![]() ��
��![]() ��T������.
��T������.![]() ��T������Ը�ⱻ���ɵ�
��T������Ը�ⱻ���ɵ�![]() �˺Ͳ�Ը�ⱻ���ɵ�
�˺Ͳ�Ը�ⱻ���ɵ�![]() �ˈ�(b��o)������,�����S�C(j��)�x��
�ˈ�(b��o)������,�����S�C(j��)�x��![]() ��,ӛ�x��Ը�ⱻ���ɵ��˔�(sh��)��
��,ӛ�x��Ը�ⱻ���ɵ��˔�(sh��)��![]() ��
��![]() ��T������Ը�ⱻ���ɵ�
��T������Ը�ⱻ���ɵ�![]() �˺Ͳ�Ը�ⱻ���ɵ�
�˺Ͳ�Ը�ⱻ���ɵ�![]() �ˈ�(b��o)������,�����S�C(j��)�x��
�ˈ�(b��o)������,�����S�C(j��)�x��![]() ��,ӛ�x��Ը�ⱻ���ɵ��˔�(sh��)��
��,ӛ�x��Ը�ⱻ���ɵ��˔�(sh��)��![]() ,��
,��![]() �ĸ��ʣ�
�ĸ��ʣ�
������(sh��)��(j��)��

��������ʽ��,����![]() ��.
��.
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com