
���}Ŀ����֪�E�A![]() ��(j��ng)�^���タ
��(j��ng)�^���タ![]() �Ľ��c(di��n)
�Ľ��c(di��n)![]() ��
��![]() �ϵ��c(di��n)
�ϵ��c(di��n)![]() �c
�c![]() �ăɂ����c(di��n)����(g��u)�ɵ������ε����L��
�ăɂ����c(di��n)����(g��u)�ɵ������ε����L��![]() ��
��
��1����![]() �ķ��̣�
�ķ��̣�
��2�����c(di��n)![]() �P(gu��n)��ԭ�c(di��n)
�P(gu��n)��ԭ�c(di��n)![]() �Č��Q�c(di��n)��
���Q�c(di��n)��![]() ���^�c(di��n)
���^�c(di��n)![]() ��ֱ��
��ֱ��![]() ��
��![]() ����һ�c(di��n)
����һ�c(di��n)![]() ����
����![]() �S���c(di��n)
�S���c(di��n)![]() ����
����![]() ��
��![]() ����
���Д�![]() �Ƿ�鶨ֵ���������ԓֵ��������Ո�f�����ɣ�
�Ƿ�鶨ֵ���������ԓֵ��������Ո�f�����ɣ�
���𰸡���1��![]() ��2���Ƕ�ֵ��
��2���Ƕ�ֵ��![]() �鶨ֵ2��
�鶨ֵ2��
��������
��1����������タ![]() �Ľ��c(di��n)
�Ľ��c(di��n)![]() ������(bi��o)������
������(bi��o)������![]() ��(j��ng)�^�c(di��n)
��(j��ng)�^�c(di��n)![]() �ó�
�ó�![]() ��ֵ��������ÙE�A�Ķ��x�Լ��}�Зl�����
��ֵ��������ÙE�A�Ķ��x�Լ��}�Зl�����![]() ���Ķ��ý⣻
���Ķ��ý⣻
��2�����O(sh��)��ֱ��![]() �ķ��̣�����c(di��n)
�ķ��̣�����c(di��n)![]() ������(bi��o)���ɵ�
������(bi��o)���ɵ�![]() ��ֵ���ٰ�
��ֵ���ٰ�![]() �ķ����c
�ķ����c![]() �ķ���(li��n)��������c(di��n)
�ķ���(li��n)��������c(di��n)![]() ������(bi��o)���Ķ���
������(bi��o)���Ķ���![]() ��ֵ������(j��)��֪���
��ֵ������(j��)��֪���![]() ������(j��)�E�A�Č��Q�ԣ����
������(j��)�E�A�Č��Q�ԣ����![]() �������Д�
�������Д�![]() �Ƿ�鶨ֵ.
�Ƿ�鶨ֵ.
��1����?y��n)钁�タ![]() �Ľ��c(di��n)
�Ľ��c(di��n)![]() ������
������![]() ��
��
��?y��n)?/span>![]() �ϵ��c(di��n)
�ϵ��c(di��n)![]() �c
�c![]() �ăɂ����c(di��n)����(g��u)�ɵ������ε����L��
�ăɂ����c(di��n)����(g��u)�ɵ������ε����L��![]() ��
��
����![]() ������
������![]() ��
��
����![]() ��
��
����![]() �ķ��̞�
�ķ��̞�![]() .
.
��2�����}���ֱ֪��![]() ��б�ʴ����Ҳ���0���O(sh��)ֱ��
��б�ʴ����Ҳ���0���O(sh��)ֱ��![]() �ķ��̞�
�ķ��̞�![]() ��
��
��![]() ����
����![]() ����
����![]() ������
������![]() ��
��
��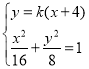 ����
����![]() �����
�����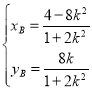 ��
��
�� �� ����
�� ����![]() ��
��
��?y��n)?/span>![]() ��
��![]() ������ֱ��
������ֱ��![]() �ķ��̞�
�ķ��̞�![]() ��
��
��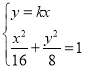 ����
����![]() �����
�����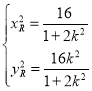 ��
��
����![]() ��
��
����(j��)�E�A�Č��Q�ԣ�֪![]() ����
����![]() ��
��
����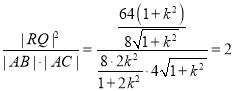 ��
��
��![]() �鶨ֵ��ԓ��ֵ��2.
�鶨ֵ��ԓ��ֵ��2.



| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪�E�A![]() ���ҽ��c(di��n)��
���ҽ��c(di��n)��![]() ���Ҝ�(zh��n)����
���Ҝ�(zh��n)����![]() .�^�c(di��n)
.�^�c(di��n)![]() ���c����(bi��o)�S������ֱ��ֱ���c�E�A
���c����(bi��o)�S������ֱ��ֱ���c�E�A![]() ����
����![]() ��
��![]() ���c(di��n)������
���c(di��n)������![]() �����c(di��n)��
�����c(di��n)��![]() ��
��![]() ������(bi��o)ԭ�c(di��n)����ֱ��
������(bi��o)ԭ�c(di��n)����ֱ��![]() �c�Ҝ�(zh��n)��
�c�Ҝ�(zh��n)��![]() �����c(di��n)
�����c(di��n)![]() .
.
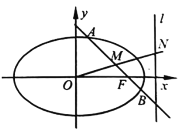
��1����E�A![]() �Ę�(bi��o)��(zh��n)���̣�
�Ę�(bi��o)��(zh��n)���̣�
��2����![]() ����ֱ��
����ֱ��![]() �ķ��̣�
�ķ��̣�
��3���Ƿ���ڌ�(sh��)��(sh��)![]() ��ʹ��
��ʹ��![]() ������������ڣ���(sh��)��(sh��)
������������ڣ���(sh��)��(sh��)![]() ��ֵ���������ڣ�Ո�f������.
��ֵ���������ڣ�Ո�f������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D��ij����һ�K�돽��R������AOB���@������O���������ڈA�ĈA�ģ�AOB��![]() ��OA��OB��
��OA��OB��![]() �鹫�@ԭ�е�·.��M�������^�p�ͽ�������Ҫ���������T�M��
�鹫�@ԭ�е�·.��M�������^�p�ͽ�������Ҫ���������T�M��![]() ���xȡһ�c(di��n)M���½���·OM���cOAƽ�еĵ�·MN���c(di��n)N�ھ���OB�ϣ����O(sh��)AOM��
���xȡһ�c(di��n)M���½���·OM���cOAƽ�еĵ�·MN���c(di��n)N�ھ���OB�ϣ����O(sh��)AOM��![]() .
.

��1������O(sh��)Ӌ������ʹ������c(di��n)O���l(f��)�ص�·OM��MN�������c(di��n)N����(j��ng)�^��·�����L��Ո�f�����ɣ�
��2������O(sh��)Ӌ������ʹ������c(di��n)A���l(f��)�ص�·![]() ��MN�������c(di��n)N����(j��ng)�^��·�����L��Ո�f������.
��MN�������c(di��n)N����(j��ng)�^��·�����L��Ո�f������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() ��
��![]() �ϵ��溯��(sh��)������
�ϵ��溯��(sh��)������![]() ���t�� ���P(gu��n)�ں���(sh��)
���t�� ���P(gu��n)�ں���(sh��)![]() �������У��������_���ǣ� ��
�������У��������_���ǣ� ��
�ٌ�����(sh��)![]() �ĈD������ƽ��
�ĈD������ƽ��![]() ����λ���Եõ�����(sh��)
����λ���Եõ�����(sh��)![]() �ĈD��
�ĈD��
�ں���(sh��)![]() �D���һ�l���Q�S���̞�
�D���һ�l���Q�S���̞�![]() ��
��
�ۮ�(d��ng)![]() �r������(sh��)
�r������(sh��)![]() ����Сֵ��
����Сֵ��![]() ��
��
�ܺ���(sh��)![]() ��
��![]() �φ��{(di��o)�f��.
�φ��{(di��o)�f��.
A.�٢�B.�ۢ�C.�ڢ�D.�ڢ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���±���ijԭ�����Ј��Ϗ�2013����2019���@7����ÿ���ƽ���r��λ��ǧԪ/������(sh��)��(j��)��
��� | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
��ݴ�̖ | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
ƽ���r�� ����λ��ǧԪ/���� |
|
|
|
|
|
|
|
��![]() ��
��![]() �������P(gu��n)���^��(qi��ng)�������
�������P(gu��n)���^��(qi��ng)�������![]() ����׃��
����׃��![]() ���A(y��)��׃���ľ��Իؚw���̣�ϵ��(sh��)���_��
���A(y��)��׃���ľ��Իؚw���̣�ϵ��(sh��)���_��![]() ����
����
��2���ԣ�1���ĽY(ji��)Փ������(j��)���A(y��)�y2032��ԓԭ�σr��.�A(y��)��ԓԭ�σr������һ��ͻ��1�fԪ/����
������(sh��)��(j��)��![]() ��
��![]() ��
��![]() ��
��![]()
������ʽ���ؚw����![]() ��б�ʺͽؾ����С���˹�Ӌ��ʽ�քe�飺
��б�ʺͽؾ����С���˹�Ӌ��ʽ�քe�飺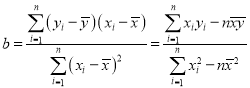 ��
��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)f(x)=aex��x��
��1����f(x)���{(di��o)�^(q��)�g��
��2�����P(gu��n)��x����ʽaex��x+b������![]() ������(sh��)b���������
������(sh��)b���������![]() ����Сֵ.
����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���O(sh��)�E�A![]() �����ҽ��c(di��n)�քe��
�����ҽ��c(di��n)�քe��![]() ������c(di��n)��
������c(di��n)��![]() ���x���ʞ�
���x���ʞ�![]() �� ��
�� ��![]() �Sؓ(f��)���S����һ�c(di��n)
�Sؓ(f��)���S����һ�c(di��n)![]() ����
����![]()
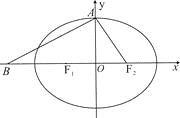
��1�����^![]() ���c(di��n)�ĈA ǡ���cֱ��
���c(di��n)�ĈA ǡ���cֱ��![]() ���У���E�AC�ķ��̣�
���У���E�AC�ķ��̣�
��2���ڣ�1���ėl���£��^�ҽ��c(di��n)![]() ��б�ʞ�
��б�ʞ�![]() ��ֱ��
��ֱ��![]() �c�E�AC����
�c�E�AC����![]() ���c(di��n)����
���c(di��n)����![]() �S���Ƿ�����c(di��n)
�S���Ƿ�����c(di��n)![]() ��ʹ����
��ʹ����![]() ����߅��ƽ����߅�������Σ�������ڣ����
����߅��ƽ����߅�������Σ�������ڣ����![]() ��ȡֵ��������������ڣ��f�����ɣ�
��ȡֵ��������������ڣ��f�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪���タ![]() �Ľ��c(di��n)��
�Ľ��c(di��n)��![]() ����(zh��n)��
����(zh��n)��![]() �c
�c![]() �S�����c(di��n)
�S�����c(di��n)![]() ���^�c(di��n)
���^�c(di��n)![]() ��ֱ�������タ��
��ֱ�������タ��![]() ��
��![]() ���c(di��n)���c(di��n)
���c(di��n)���c(di��n)![]() �ڵ�һ����.
�ڵ�һ����.
![]() ��
��![]() ��
��![]() ����ֱ��
����ֱ��![]() �ķ��̣�
�ķ��̣�
![]() ��
��![]() ���c(di��n)
���c(di��n)![]() ���(zh��n)��
���(zh��n)��![]() ������һ�c(di��n)�����C��ֱ��
������һ�c(di��n)�����C��ֱ��![]() ��
��![]() ��
��![]() ��б�ʳɵȲ(sh��)��.
��б�ʳɵȲ(sh��)��.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��ij�N�ί����ڠ����Ⱦ���ď�(f��)����ˎ�a(ch��n)Ʒ���|(zh��)�������|(zh��)��ָ��(bi��o)ֵ�������|(zh��)��ָ��(bi��o)Խ������|(zh��)��Խ�ã�������߮a(ch��n)Ʒ�|(zh��)�����҇��t(y��)�����Ќ��ҹ��Կ��y�����аl(f��)��![]() ��
��![]() �ɷN���䷽���ڃɷN���䷽���a(ch��n)�Įa(ch��n)Ʒ���S�C(j��)��ȡ��(sh��)����ͬ�Ęӱ����y���@Щ�a(ch��n)Ʒ���|(zh��)��ָ��(bi��o)ֵ��Ҏ(gu��)��ָ��(bi��o)ֵС��
�ɷN���䷽���ڃɷN���䷽���a(ch��n)�Įa(ch��n)Ʒ���S�C(j��)��ȡ��(sh��)����ͬ�Ęӱ����y���@Щ�a(ch��n)Ʒ���|(zh��)��ָ��(bi��o)ֵ��Ҏ(gu��)��ָ��(bi��o)ֵС��![]() �r��UƷ��ָ��(bi��o)ֵ��
�r��UƷ��ָ��(bi��o)ֵ��![]() ��һ��Ʒ������
��һ��Ʒ������![]() ���ص�Ʒ���F(xi��n)�ќy����(sh��)��(j��)�������£�����
���ص�Ʒ���F(xi��n)�ќy����(sh��)��(j��)�������£�����![]() �䷽�UƷ��
�䷽�UƷ��![]() ����
����
![]() �䷽���l��(sh��)�ֲ���
�䷽���l��(sh��)�ֲ���
�|(zh��)��ָ��(bi��o)ֵ�ֽM |
|
|
|
|
|
�l��(sh��) |
|
|
|
|
|

��1����![]() ��
��![]() ��ֵ��
��ֵ��
��2��ԇ�_��![]() �䷽��
�䷽��![]() �䷽��һ�N�ã�(�f�����ڽy(t��ng)Ӌ�����У�ͬһ�M��(sh��)��(j��)����ԓ�M�^(q��)�g�����c(di��n)ֵ�������)
�䷽��һ�N�ã�(�f�����ڽy(t��ng)Ӌ�����У�ͬһ�M��(sh��)��(j��)����ԓ�M�^(q��)�g�����c(di��n)ֵ�������)
�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��ƽ�_ | �W(w��ng)���к���Ϣ�e�^(q��) | ����p�_�e�^(q��) | ��vʷ̓�o���x�к���Ϣ�e�^(q��) | �����֙�(qu��n)�e�^(q��)
�`���Ͳ�����Ϣ�e���Ԓ��027-86699610 �e���]�䣺58377363@163.com