
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 為矩形,
為矩形, ![]() ,
,
![]() .
.

(1)求直線![]() 與平面
與平面![]() 所成角的正弦值;
所成角的正弦值;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】試題分析:(1)根據(jù)條件建立空間直角坐標系,設立各點坐標,列方程組求出平面一個法向量,利用向量數(shù)量積求直線方向向量與法向量夾角,最后根據(jù)線面角與向量夾角關系求直線![]() 與平面
與平面![]() 所成角的正弦值;(2)列方程組求出兩個平面法向量,利用向量數(shù)量積求法向量夾角,最后根據(jù)二面角與法向量夾角關系確定二面角
所成角的正弦值;(2)列方程組求出兩個平面法向量,利用向量數(shù)量積求法向量夾角,最后根據(jù)二面角與法向量夾角關系確定二面角![]() 的余弦值.
的余弦值.
試題解析:∵![]() ,∴
,∴![]() 底面
底面![]() ,又底面
,又底面![]() 為矩形,∴分別以
為矩形,∴分別以![]() 為
為![]() 軸、
軸、![]() 軸、
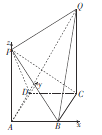
軸、![]() 軸,建立如圖所示的空間直角坐標系,則
軸,建立如圖所示的空間直角坐標系,則![]() .
.
∴![]() .
.
(1)設平面![]() 的一個法向量
的一個法向量![]() ,
,
則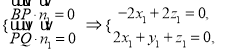 令
令![]() ,得
,得 ![]() ,
,
∴![]() 與平面
與平面![]() 所成角的正弦值
所成角的正弦值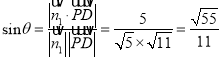 .
.
(2)設平面![]() 的一個法向量
的一個法向量![]() ,
,
則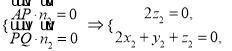 令
令![]() ,得
,得 ![]() ,
,
∴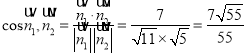 ,∴二面角
,∴二面角![]() 的余弦值為
的余弦值為![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數(shù)學 來源: 題型:
【題目】數(shù)學家歐拉1765年在其所著的《三角形幾何學》一書中提出:任意三角形的外心、重心、垂心在同一條直線上,后人稱這條直線為歐拉線.已知△ABC的頂點A(2,0),B(0,4),若其歐拉線的方程為x-y+2=0,則頂點C的坐標是( )
A. (-4,0) B. (0,-4) C. (4,0) D. (4,0)或(-4,0)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
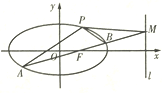
【題目】如圖,橢圓![]() 經(jīng)過點
經(jīng)過點![]() ,離心率
,離心率![]() ,直線
,直線![]() 的方程為
的方程為![]() .
.
![]() 求橢圓
求橢圓![]() 的方程;
的方程;
![]()
![]() 是經(jīng)過右焦點
是經(jīng)過右焦點![]() 的任一弦(不經(jīng)過點
的任一弦(不經(jīng)過點![]() ),設直線
),設直線![]() 與直線
與直線![]() 相交于點
相交于點![]() ,記
,記![]() ,
, ![]() ,
, ![]() 的斜率為
的斜率為![]() ,
, ![]() ,
, ![]() .問:是否存在常數(shù)
.問:是否存在常數(shù)![]() ,使得
,使得![]() ?若存在,求
?若存在,求![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知數(shù)列{an}的前n項和是Sn,且Sn![]() =1(n∈N),數(shù)列{bn}是公差d不等于0的等差數(shù)列,且滿足:b1=
=1(n∈N),數(shù)列{bn}是公差d不等于0的等差數(shù)列,且滿足:b1=![]() ,而b2,b5,ba14成等比數(shù)列.
,而b2,b5,ba14成等比數(shù)列.
(1)求數(shù)列{an}、{bn}的通項公式;
(2)設cn=anbn,求數(shù)列{cn}的前n項和Tn.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知![]() ,
,![]() 是平面,
是平面,![]() ,
,![]() 是直線,給出下列命題:
是直線,給出下列命題:
①若![]() ,
,![]() ,則
,則![]() ;
;
②若![]() ,
,![]() ,
,![]() ,
,![]() ,則
,則![]() ;
;
③如果![]() ,
,![]() ,
,![]() ,
,![]() 是異面直線,則
是異面直線,則![]() 與
與![]() 相交;
相交;
④若![]() .
.![]() ,且
,且![]() ,
,![]() ,則
,則![]() ,且
,且![]()
其中正確確命題的序號是_____(把正確命題的序號都填上)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,上頂點
,上頂點![]() 到直線
到直線![]() 的距離為
的距離為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)是否存在過點![]() 的直線
的直線![]() 與橢圓交于不同的兩點
與橢圓交于不同的兩點![]() ,線段
,線段![]() 的中點為
的中點為![]() ,使得
,使得![]() ?若存在,求直線
?若存在,求直線![]() 的方程;若不存在,請說明理由.
的方程;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】給出下列命題:①若![]() ,則
,則![]() ;②若
;②若![]() ,
,![]() ,則
,則![]() ;③若
;③若![]() ,則
,則![]() ;④
;④![]() ;⑤若
;⑤若![]() ,
,![]() ,則
,則![]() ,
,![]() ;⑥正數(shù)
;⑥正數(shù)![]() ,
,![]() 滿足
滿足![]() ,則
,則![]() 的最小值為
的最小值為![]() .其中正確命題的序號是__________.
.其中正確命題的序號是__________.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分別在
分別在![]() ,
,![]() 上,
上,![]() ,現(xiàn)將四邊形
,現(xiàn)將四邊形![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() .
.
(Ⅰ)若![]() ,在折疊后的線段
,在折疊后的線段![]() 上是否存在一點
上是否存在一點![]() ,且
,且![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,說明理由;
的值;若不存在,說明理由;
(Ⅱ)求三棱錐![]() 的體積的最大值.
的體積的最大值.

查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com