
【題目】已知數(shù)列{an}的前n項和是Sn,且Sn![]() =1(n∈N),數(shù)列{bn}是公差d不等于0的等差數(shù)列,且滿足:b1=
=1(n∈N),數(shù)列{bn}是公差d不等于0的等差數(shù)列,且滿足:b1=![]() ,而b2,b5,ba14成等比數(shù)列.
,而b2,b5,ba14成等比數(shù)列.
(1)求數(shù)列{an}、{bn}的通項公式;
(2)設(shè)cn=anbn,求數(shù)列{cn}的前n項和Tn.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]()
【解析】分析:(I)Sn![]() =1(n∈N),n≥2時,Sn﹣1+
=1(n∈N),n≥2時,Sn﹣1+![]() an﹣1=1,相減可得:an
an﹣1=1,相減可得:an![]() ﹣
﹣![]() an﹣1=0,化為:an=
an﹣1=0,化為:an=![]() an﹣1.利用等比數(shù)列的通項公式可得an.?dāng)?shù)列{bn}是公差d不等于0的等差數(shù)列,且滿足:b1=
an﹣1.利用等比數(shù)列的通項公式可得an.?dāng)?shù)列{bn}是公差d不等于0的等差數(shù)列,且滿足:b1=![]() =1.由b2,b5,b14成等比數(shù)列.可得
=1.由b2,b5,b14成等比數(shù)列.可得![]() =b2b14,(1+4d)2=(1+d)(1+13d),d≠0.解得d.即可得出;(Ⅱ)設(shè)cn=anbn=
=b2b14,(1+4d)2=(1+d)(1+13d),d≠0.解得d.即可得出;(Ⅱ)設(shè)cn=anbn=![]() ,利用錯位相減法即可得出.
,利用錯位相減法即可得出.
詳解:
(1)Sn![]() =1(n∈N),n≥2時,Sn﹣1+
=1(n∈N),n≥2時,Sn﹣1+![]() an﹣1=1,相減可得:an
an﹣1=1,相減可得:an![]() ﹣
﹣![]() an﹣1=0,化為:an=
an﹣1=0,化為:an=![]() an﹣1.
an﹣1.
n=1時,a1+![]() =1,解得a1=
=1,解得a1=![]() .
.
∴數(shù)列{an}是等比數(shù)列,首項為![]() ,公比為
,公比為![]() .∴an=
.∴an=![]() =2×
=2×![]() .
.
數(shù)列{bn}是公差d不等于0的等差數(shù)列,且滿足:b1=![]() =1.
=1.
∵b2,b5,b14成等比數(shù)列.∴![]() =b2b14,
=b2b14,
∴(1+4d)2=(1+d)(1+13d),d≠0.解得d=2.∴bn=1+2(n﹣1)=2n﹣1.
(2)設(shè)cn=anbn=![]() .
.
求數(shù)列{cn}的前n項和Tn=![]() +……+
+……+![]() .
.
![]() =
=![]() +……+
+……+![]() +
+![]() ,
,
相減可得:![]() Tn=
Tn=![]() +4
+4![]() ﹣
﹣![]() =
=![]() +4×
+4×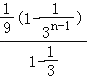 ﹣
﹣![]() ,
,
化為:Tn=2﹣![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() 是圓
是圓![]() 上任意一點,過
上任意一點,過![]() 作
作![]() 軸的垂線段
軸的垂線段![]() ,
, ![]() 為垂足.當(dāng)點
為垂足.當(dāng)點![]() 在圓
在圓![]() 上運動時,線段
上運動時,線段![]() 中點
中點![]() 的軌跡為曲線
的軌跡為曲線![]() (包括點
(包括點![]() 和點
和點![]() ),
),![]() 為坐標(biāo)原點.
為坐標(biāo)原點.
(Ⅰ)求曲線![]() 的方程;
的方程;
(Ⅱ)直線![]() 與曲線
與曲線![]() 相切,且
相切,且![]() 與圓
與圓![]() 相交于
相交于![]() 兩點,當(dāng)
兩點,當(dāng)![]() 的面積最大時,試求直線
的面積最大時,試求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,其中
,其中![]()
(1)當(dāng)![]() 時,求函數(shù)
時,求函數(shù)![]() 在
在![]() 處的切線方程;
處的切線方程;
(2)若函數(shù)![]() 在定義域上有且只有一個極值點,求實數(shù)
在定義域上有且只有一個極值點,求實數(shù)![]() 的取值范圍;
的取值范圍;
(3)若對任意![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某校學(xué)生研究學(xué)習(xí)小組發(fā)現(xiàn),學(xué)生上課的注意力指標(biāo)隨著聽課時間的變化而變化,老師講課開始時,學(xué)生的興趣激增;接下來學(xué)生的興趣將保持較理想的狀態(tài)一段時間,隨后學(xué)生的注意力開始分散.設(shè)![]() 表示學(xué)生注意力指標(biāo).
表示學(xué)生注意力指標(biāo).
該小組發(fā)現(xiàn)![]() 隨時間
隨時間![]() (分鐘)的變化規(guī)律(
(分鐘)的變化規(guī)律(![]() 越大,表明學(xué)生的注意力越集中)如下:
越大,表明學(xué)生的注意力越集中)如下: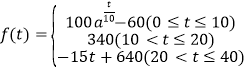 (
(![]() 且
且![]() ).
).
若上課后第![]() 分鐘時的注意力指標(biāo)為
分鐘時的注意力指標(biāo)為![]() ,回答下列問題:
,回答下列問題:
(![]() )求
)求![]() 的值.
的值.
(![]() )上課后第
)上課后第![]() 分鐘和下課前
分鐘和下課前![]() 分鐘比較,哪個時間注意力更集中?并請說明理由.
分鐘比較,哪個時間注意力更集中?并請說明理由.
(![]() )在一節(jié)課中,學(xué)生的注意力指標(biāo)至少達到
)在一節(jié)課中,學(xué)生的注意力指標(biāo)至少達到![]() 的時間能保持多長?
的時間能保持多長?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
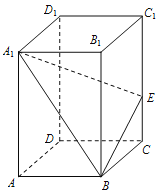
【題目】如圖,已知長方體ABCD-A1B1C1D1中,AB=3,BC=2,CC1=5,E是棱CC1上不同于端點的點,且![]() .
.
(1) 當(dāng)∠BEA1為鈍角時,求實數(shù)λ的取值范圍;
(2) 若λ=![]() ,記二面角B1-A1B-E的的大小為θ,求|cosθ|.
,記二面角B1-A1B-E的的大小為θ,求|cosθ|.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
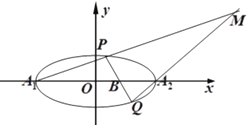
【題目】如圖,已知橢圓![]() 的右準(zhǔn)線
的右準(zhǔn)線![]() 的方程為
的方程為![]() ,焦距為
,焦距為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)過定點![]() 作直線
作直線![]() 與橢圓
與橢圓![]() 交于點
交于點![]() (異于橢圓
(異于橢圓![]() 的左、右頂點
的左、右頂點![]() )兩點,設(shè)直線
)兩點,設(shè)直線![]() 與直線
與直線![]() 相交于點
相交于點![]() .
.
①若![]() ,試求點
,試求點![]() 的坐標(biāo);
的坐標(biāo);
②求證:點![]() 始終在一條直線上.
始終在一條直線上.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(本題滿分12分)已知極坐標(biāo)系的極點與直角坐標(biāo)系的原點重合,極軸與直角坐標(biāo)系的x軸的正半軸重合,且兩個坐標(biāo)系的單位長度相同.已知直線l的參數(shù)方程為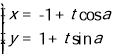 (t為參數(shù)),曲線C的極坐標(biāo)方程為
(t為參數(shù)),曲線C的極坐標(biāo)方程為![]() .
.
(Ⅰ)若直線l的斜率為-1,求直線l與曲線C交點的極坐標(biāo);
(Ⅱ)若直線l與曲線C相交弦長為![]() ,求直線l的參數(shù)方程(標(biāo)準(zhǔn)形式).
,求直線l的參數(shù)方程(標(biāo)準(zhǔn)形式).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓E: ![]() 的左焦點為
的左焦點為![]() ,且過點
,且過點 .
.

(Ⅰ)求橢圓E的方程;
(Ⅱ)設(shè)直線![]() 與橢圓E交于
與橢圓E交于![]() 兩點,與
兩點,與![]() 的交點為
的交點為![]() ,且滿足.
,且滿足. ![]()
![]()
①若![]() ,求:
,求: ![]() 的值;
的值;
②設(shè)點![]() 是橢圓E的左頂點,點
是橢圓E的左頂點,點![]() 關(guān)于
關(guān)于![]() 軸的對稱點為點
軸的對稱點為點![]() ,試探究:在線段
,試探究:在線段![]() 上是否存在一個定點
上是否存在一個定點![]() ,使得直線
,使得直線![]() 過定點
過定點![]() ,如果存在,求出點
,如果存在,求出點![]() 的坐標(biāo);如果不存在,請說明理由。
的坐標(biāo);如果不存在,請說明理由。
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com