
【題目】已知某產(chǎn)品的銷售額![]() 與廣告費(fèi)用
與廣告費(fèi)用![]() 之間的關(guān)系如下表:
之間的關(guān)系如下表:
| 0 | 1 | 2 | 3 | 4 |
| 10 | 15 |
| 30 | 35 |
若根據(jù)表中的數(shù)據(jù)用最小二乘法求得![]() 對
對![]() 的回歸直線方程為
的回歸直線方程為![]() ,則下列說法中錯誤的是( )
,則下列說法中錯誤的是( )
A.產(chǎn)品的銷售額與廣告費(fèi)用成正相關(guān)
B.該回歸直線過點(diǎn)![]()
C.當(dāng)廣告費(fèi)用為10萬元時,銷售額一定為74萬元
D.![]() 的值是20
的值是20
 中考利劍中考試卷匯編系列答案
中考利劍中考試卷匯編系列答案 教育世家狀元卷系列答案
教育世家狀元卷系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() 在
在![]() 處取得極值.
處取得極值.
(1)求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)若函數(shù)![]() 在
在![]() 上恰有兩個不同的零點(diǎn),求實數(shù)
上恰有兩個不同的零點(diǎn),求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】對于定義在![]() 上的函數(shù)
上的函數(shù)![]() ,若函數(shù)
,若函數(shù)![]() 滿足:①在區(qū)間
滿足:①在區(qū)間![]() 上單調(diào)遞減,②存在常數(shù)
上單調(diào)遞減,②存在常數(shù)![]() ,使其值域為
,使其值域為![]() ,則稱函數(shù)
,則稱函數(shù)![]() 是函數(shù)
是函數(shù)![]() 的“漸近函數(shù)”.
的“漸近函數(shù)”.
(1)判斷函數(shù)![]() 是不是函數(shù)
是不是函數(shù)![]() 的“漸近函數(shù)”,說明理由;
的“漸近函數(shù)”,說明理由;
(2)求證:函數(shù)![]() 不是函數(shù)
不是函數(shù)![]() 的“漸近函數(shù)”;
的“漸近函數(shù)”;
(3)若函數(shù)![]() ,
,![]() ,求證:當(dāng)且僅當(dāng)
,求證:當(dāng)且僅當(dāng)![]() 時,
時,![]() 是
是![]() 的“漸近函數(shù)”.
的“漸近函數(shù)”.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四棱錐![]() 中,已知
中,已知![]() 平面
平面![]() ,且四邊形
,且四邊形![]() 為直角梯形,
為直角梯形,![]() ,
,![]() ,
,![]() .
.
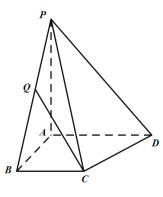
(Ⅰ)求平面![]() 與平面
與平面![]() 所成二面角(銳角)的余弦值;
所成二面角(銳角)的余弦值;
(Ⅱ)點(diǎn)![]() 是線段
是線段![]() 上的動點(diǎn),當(dāng)直線
上的動點(diǎn),當(dāng)直線![]() 與
與![]() 所成角最小時,求線段
所成角最小時,求線段![]() 的長度.
的長度.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】點(diǎn)P是棱長為1的正方體ABCD﹣A1B1C1D1的底面A1B1C1D1上一點(diǎn),則![]() 的取值范圍是__.
的取值范圍是__.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】若存在實數(shù)![]() 使得
使得![]() 則稱
則稱![]() 是區(qū)間
是區(qū)間![]() 的
的![]() 一內(nèi)點(diǎn).
一內(nèi)點(diǎn).
(1)求證:![]() 的充要條件是存在
的充要條件是存在![]() 使得
使得![]() 是區(qū)間
是區(qū)間![]() 的
的![]() 一內(nèi)點(diǎn);
一內(nèi)點(diǎn);
(2)若實數(shù)![]() 滿足:
滿足:![]() 求證:存在
求證:存在![]() ,使得
,使得![]() 是區(qū)間
是區(qū)間![]() 的
的![]() 一內(nèi)點(diǎn);
一內(nèi)點(diǎn);
(3)給定實數(shù)![]() ,若對于任意區(qū)間
,若對于任意區(qū)間![]() ,
,![]() 是區(qū)間的
是區(qū)間的![]() 一內(nèi)點(diǎn),
一內(nèi)點(diǎn),![]() 是區(qū)間的
是區(qū)間的![]() 一內(nèi)點(diǎn),且不等式
一內(nèi)點(diǎn),且不等式![]() 和不等式
和不等式![]() 對于任意
對于任意![]() 都恒成立,求證:
都恒成立,求證:![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】有一塊三角形邊角地,如圖![]() ,
,![]() ,
,![]() ,
,![]() .(單位為百米).欲利用這塊地修一個三角形形狀的草坪(圖中
.(單位為百米).欲利用這塊地修一個三角形形狀的草坪(圖中![]() )供市民休閑,其中點(diǎn)
)供市民休閑,其中點(diǎn)![]() 在邊
在邊![]() 上,點(diǎn)
上,點(diǎn)![]() 在邊
在邊![]() 上,沿
上,沿![]() 的三邊修建休閑長廊,規(guī)劃部門要求
的三邊修建休閑長廊,規(guī)劃部門要求![]() 的面積占
的面積占![]() 面積的一半,設(shè)
面積的一半,設(shè)![]() (百米),
(百米),![]() 的周長為
的周長為![]() (百米)
(百米)

(1)求出![]() 函數(shù)的解析式及定義域
函數(shù)的解析式及定義域
(2)求出休閑長廊總長度![]() 的取值范圍,并確定當(dāng)
的取值范圍,并確定當(dāng)![]() 取到最大值時點(diǎn)
取到最大值時點(diǎn)![]() ,
,![]() 的位置
的位置
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】給出下列命題:
(1)存在實數(shù)![]() 使
使![]() ;
;
(2)直線![]() 是函數(shù)
是函數(shù)![]() 圖象的一條對稱軸;
圖象的一條對稱軸;
(3)![]() (
(![]() )的值域是
)的值域是![]() ;
;
(4)若![]() ,
,![]() 都是第一象限角,且
都是第一象限角,且![]() ,則
,則![]() .
.
其中正確命題的序號為( )
A.(1)(2)B.(2)(3)C.(3)(4)D.(1)(4)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)![]() ,
,![]() 是兩條不同的直線,
是兩條不同的直線,![]() ,
,![]() ,
,![]() 是三個不同的平面,給出下列四個命題:
是三個不同的平面,給出下列四個命題:
①若![]() ,
,![]() ,則
,則![]()
②若![]() ,
,![]() ,
,![]() ,則
,則![]()
③若![]() ,
,![]() ,則
,則![]()
④若![]() ,
,![]() ,則
,則![]()
其中正確命題的序號是( )
A.①和②B.②和③C.③和④D.①和④
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com