
【題目】2019超長“三伏”來襲,雖然大部分人都了解“伏天”不宜吃生冷食物,但隨著氣溫的不斷攀升,仍然無法阻擋冷飲品銷量的暴增.現在,某知名冷飲品銷售公司通過隨機抽樣的方式,得到其100家加盟超市3天內進貨總價的統計結果如下表所示:
組別(單位:百元) |
|
|
|
|
|
|
頻數 | 3 | 11 | 20 | 27 | 26 | 13 |
(1)由頻數分布表大致可以認為,被抽查超市3天內進貨總價![]() ,μ近似為這100家超市3天內進貨總價的平均值(同一組中的數據用該組區間的中點值作代表),利用正態分布,求
,μ近似為這100家超市3天內進貨總價的平均值(同一組中的數據用該組區間的中點值作代表),利用正態分布,求![]() ;
;
(2)在(1)的條件下,該公司為增加銷售額,特別為這100家超市制定如下抽獎方案:
①令m表示“超市3天內進貨總價超過μ的百分點”,其中![]() .若
.若![]() ,則該超市獲得1次抽獎機會;
,則該超市獲得1次抽獎機會;![]() ,則該超市獲得2次抽獎機會;
,則該超市獲得2次抽獎機會;![]() ,則該超市獲得3次抽獎機會;
,則該超市獲得3次抽獎機會;![]() ,則該超市獲得4次抽獎機會;
,則該超市獲得4次抽獎機會;![]() ,則該超市獲得5次抽獎機會;
,則該超市獲得5次抽獎機會;![]() ,則該超市獲得6次抽獎機會.另外,規定3天內進貨總價低于μ的超市沒有抽獎機會;
,則該超市獲得6次抽獎機會.另外,規定3天內進貨總價低于μ的超市沒有抽獎機會;
②每次抽獎中獎獲得的獎金金額為1000元,每次抽獎中獎的概率為![]() .
.
設超市A參加了抽查,且超市A在3天內進貨總價![]() 百元.記X(單位:元)表示超市A獲得的獎金總額,求X的分布列與數學期望.
百元.記X(單位:元)表示超市A獲得的獎金總額,求X的分布列與數學期望.
附參考數據與公式:![]() ,若
,若![]() ,則
,則![]() ,
,![]() ,
,![]() .
.
科目:高中數學 來源: 題型:
【題目】已知f(x)=ax2+bx+c(a≠0),滿足條件f(x+1)-f(x)=2x(x∈R),且f(0)=1.
(Ⅰ)求f(x)的解析式;
(Ⅱ)當x≥0時,f(x)≥mx-3恒成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】過橢圓E:![]() 1(a>b>0)上一動點P向圓O:x2+y2=b2引兩條切線PA,PB,切點分別是A,B.直線AB分別與x軸,y軸交于點M,N(O為坐標原點).
1(a>b>0)上一動點P向圓O:x2+y2=b2引兩條切線PA,PB,切點分別是A,B.直線AB分別與x軸,y軸交于點M,N(O為坐標原點).

(1)若在橢圓E上存在點P,滿足PA⊥PB,求橢圓E的離心率的取值范圍;
(2)求證:在橢圓E內,存在一點C滿足|CO|=|CA|=|CP|=|CB|;
(3)若橢圓E的短軸長為2,△MON面積的最小值為![]() ,求橢圓E的方程.
,求橢圓E的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】又到了品嘗小龍蝦的季節,小龍蝦近幾年來被稱作是“國民宵夜”風靡國內外.在巨大的需求市場下,湖北的小龍蝦產量占據了全國的半壁江山,湖北某地區近幾年的小龍蝦產量統計如下表:
年份 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代碼 | 1 | 2 | 3 | 4 | 5 | 6 |
年產量 | 6.6 | 6.9 | 7.4 | 7.7 | 8 | 8.4 |
(1)根據表中數據,建立![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(2)根據線性回歸方程預測2019年該地區農產品的年產量.
附:對于一組數據![]() ,
,![]() ,…,
,…,![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為:
的斜率和截距的最小二乘估計分別為: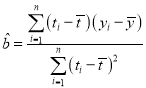 ,
,![]() .(參考數據:
.(參考數據:![]() ,計算結果保留小數點后兩位).
,計算結果保留小數點后兩位).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】汕尾市基礎教育處為調查在校中學生每天放學后的自學時間情況,在本市的所有中學生中隨機抽取了120名學生進行調查,現將日均自學時間小于1小時的學生稱為“自學不足”者![]() 根據調查結果統計后,得到如下
根據調查結果統計后,得到如下![]() 列聯表,已知在調查對象中隨機抽取1人,為“自學不足”的概率為
列聯表,已知在調查對象中隨機抽取1人,為“自學不足”的概率為![]() .
.
非自學不足 | 自學不足 | 合計 | |
配有智能手機 | 30 | ||
沒有智能手機 | 10 | ||
合計 |
![]() 請完成上面的列聯表;
請完成上面的列聯表;
![]() 根據列聯表的數據,能否有
根據列聯表的數據,能否有![]() 的把握認為“自學不足”與“配有智能手機”有關?
的把握認為“自學不足”與“配有智能手機”有關?
附表及公式: ![]() ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】由于近幾年我國多地區的霧霾天氣,引起口罩熱銷,某廠家擬在2017年舉行促銷活動,經調查該批口罩銷售量![]() 萬件(生產量與銷售量相等)與促銷費用
萬件(生產量與銷售量相等)與促銷費用![]() 萬元滿足
萬元滿足![]() (其中
(其中![]() ,
,![]() 為常數).已知生產該批口罩還要投入成本
為常數).已知生產該批口罩還要投入成本![]() 萬元(不包含促銷費用),口罩的銷售價格定為
萬元(不包含促銷費用),口罩的銷售價格定為![]() 元/件.
元/件.
(1)將該批口罩的利潤![]() 萬元表示為促銷費用
萬元表示為促銷費用![]() 萬元的函數;
萬元的函數;
(2)當促銷費用投入多少萬元時,該廠家的利潤最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線方程為y2=-4x,直線l的方程為2x+y-4=0,在拋物線上有一動點A,點A到y軸的距離為m,到直線l的距離為n,則m+n的最小值為________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】高一(1)班參加校生物競賽學生的成績的莖葉圖和頻率分布直方圖都受到不同程度的破壞,但可見部分如下,據此解答如下問題:

(1)求高一(1)班參加校生物競賽的人數及分數在[80,90)之間的頻數,并計算頻率分布直方圖中[80,90)間的矩形的高;
(2)若要從分數在[80,100]之間的學生中任選2人進行某項研究,求至少有1人分數在[90,100]之間的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角△ABC中,AC=![]() ,BC=1,點D是斜邊AB上的動點,將△BCD沿著CD翻折至△B'CD,使得點B'在平面ACD內的射影H恰好落在線段CD上,則翻折后|AB'|的最小值是_____.
,BC=1,點D是斜邊AB上的動點,將△BCD沿著CD翻折至△B'CD,使得點B'在平面ACD內的射影H恰好落在線段CD上,則翻折后|AB'|的最小值是_____.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com