
【題目】在四棱錐P-ABCD中,底面ABCD為直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,且平面
,且平面![]() 平面ABCD.
平面ABCD.
(1)求證:![]() ;
;
(2)在線段PA上是否存在一點M,使二面角M-BC-D的大小為![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
【答案】(1)證明見解析;(2)存在,![]() .
.
【解析】
(1) 過點P在面PAD內(nèi)作![]() ,垂足為O,連接BO、OC,可得
,垂足為O,連接BO、OC,可得![]() ,再結(jié)已知條件可得
,再結(jié)已知條件可得![]() 是等邊三角形,進而判斷出四邊形OBCD是正方形,從而得
是等邊三角形,進而判斷出四邊形OBCD是正方形,從而得![]() 面POC,
面POC,
得![]() ;
;
(2)由于![]() 面ABCD,
面ABCD,![]() ,所以以O坐標原點建立空間直角坐標系,設(shè)
,所以以O坐標原點建立空間直角坐標系,設(shè)![]() ,則點M的坐標為
,則點M的坐標為![]() ,求出平面MBC和平面ABCD的法向量
,求出平面MBC和平面ABCD的法向量![]() ,用
,用 ,求出
,求出![]() 的值,從而得到
的值,從而得到![]() 的值
的值
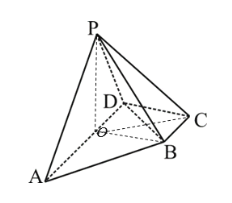
(1)證明:過點P在面PAD內(nèi)作![]() ,垂足為O,連接BO、OC
,垂足為O,連接BO、OC
∵面![]() 面ABCD,
面ABCD,
∴![]() 面ABCD,∴
面ABCD,∴![]()
∵![]() ,
,![]() ,
,
∴![]() 是等邊三角形,∴
是等邊三角形,∴![]()
又∵![]() ,
,![]()
∴四邊形OBCD是正方形,∴![]() ,
,
又![]() ,∴
,∴![]() 面POC,
面POC,
又![]() 面POC,∴
面POC,∴![]() .
.
(2)∵![]() 面ABCD,
面ABCD,![]() ,如圖,建立空間直角坐標系
,如圖,建立空間直角坐標系![]() ﹐
﹐
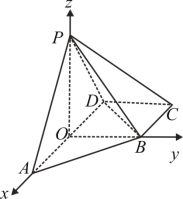
則![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
假設(shè)在線段PA上存在一點M,使二面角![]() 大小為
大小為![]()
設(shè)![]() ,
,![]() ,則
,則![]() ,
,
所以![]() ,
,
∴![]() ,
,![]() ,
,
設(shè)面MBC的法向量為![]() ,
,
則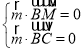 ,即
,即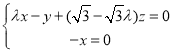 ,令
,令![]() ,得
,得![]() ,
,
所以![]() ,面ABCD的一個法向量為
,面ABCD的一個法向量為![]()
∵二面角M-BC-D大小為![]() ,
,
∴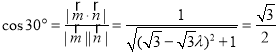
∴![]() 或
或![]() (舍),
(舍),
所以在線段PA上存在點M滿足題設(shè)條件且![]() .
.


科目:高中數(shù)學 來源: 題型:
【題目】已知焦點在![]() 軸上的拋物線
軸上的拋物線![]() 過點
過點![]() ,橢圓
,橢圓![]() 的兩個焦點分別為
的兩個焦點分別為![]() ,其中
,其中![]() 與
與![]() 的焦點重合,過
的焦點重合,過![]() 與長軸垂直的直線交橢圓
與長軸垂直的直線交橢圓![]() 于
于![]() 兩點且
兩點且![]() ,曲線
,曲線![]() 是以原點為圓心以
是以原點為圓心以![]() 為半徑的圓.
為半徑的圓.
(1)求![]() 與
與![]() 及
及![]() 的方程;
的方程;
(2)若動直線![]() 與圓
與圓![]() 相切,且與
相切,且與![]() 交與
交與![]() 兩點,三角形
兩點,三角形![]() 的面積為
的面積為![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
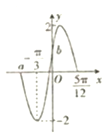
【題目】函數(shù)f(x)=Asin(2ωx+φ)(A>0,ω>0,|φ|<![]() )的部分圖象如圖所示
)的部分圖象如圖所示
(1)求A,ω,φ的值;
(2)求圖中a,b的值及函數(shù)f(x)的遞增區(qū)間;
(3)若α∈[0,π],且f(α)=![]() ,求α的值.
,求α的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】關(guān)于函數(shù)f(x)![]() (x∈R),有下述四個結(jié)論:
(x∈R),有下述四個結(jié)論:
①任意x∈R,等式f(﹣x)+f(x)=0恒成立;
②任意x1,x2∈R,若x1≠x2,則一定有f(x1)≠f(x2);
③存在m∈(0,1),使得方程|f(x)|=m有兩個不等實數(shù)根;
④存在k∈(1,+∞),使得函數(shù)g(x)=f(x)﹣kx在R上有三個零點.
其中包含了所有正確結(jié)論編號的選項為( )
A.①②③④B.①②③C.①②④D.①②
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】若函數(shù)![]() ,當
,當![]() 時,函數(shù)
時,函數(shù)![]() 有極值
有極值![]() .
.
(1)求函數(shù)![]() 的解析式;
的解析式;
(2)求函數(shù)![]() 的極值;
的極值;
(3)若關(guān)于![]() 的方程
的方程![]() 有三個不同的實數(shù)解,求實數(shù)
有三個不同的實數(shù)解,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】函數(shù)![]() 的部分圖象如圖所示,則下列敘述正確的是( )
的部分圖象如圖所示,則下列敘述正確的是( )
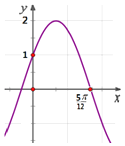
A.函數(shù)![]() 的圖象可由
的圖象可由![]() 的圖象向左平移
的圖象向左平移![]() 個單位得到
個單位得到
B.函數(shù)![]() 的圖象關(guān)于直線
的圖象關(guān)于直線![]() 對稱
對稱
C.函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上是單調(diào)遞增的
上是單調(diào)遞增的
D.函數(shù)![]() 圖象的對稱中心為
圖象的對稱中心為![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】甲、乙二人獨立破譯同一密碼,甲破譯密碼的概率為![]() ,乙破譯密碼的概率為
,乙破譯密碼的概率為![]() .記事件A:甲破譯密碼,事件B:乙破譯密碼.
.記事件A:甲破譯密碼,事件B:乙破譯密碼.
(1)求甲、乙二人都破譯密碼的概率;
(2)求恰有一人破譯密碼的概率;
(3)小明同學解答“求密碼被破譯的概率”的過程如下:
解:“密碼被破譯”也就是“甲、乙二人中至少有一人破譯密碼”所以隨機事件“密碼被破譯”可以表示為![]() 所以
所以![]()
請指出小明同學錯誤的原因?并給出正確解答過程.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】![]() 年,“非典”爆發(fā),以鐘南山為代表的醫(yī)護工作者經(jīng)長期努力,抗擊了非典.
年,“非典”爆發(fā),以鐘南山為代表的醫(yī)護工作者經(jīng)長期努力,抗擊了非典.![]() 年
年![]() 歲高齡的鐘院士再次披掛上陣,逆行武漢抗擊新冠疫情。為調(diào)查中學生對這一偉大“逆行者”的了解程度,某調(diào)查小組隨機抽取了某市物化生、政史地的
歲高齡的鐘院士再次披掛上陣,逆行武漢抗擊新冠疫情。為調(diào)查中學生對這一偉大“逆行者”的了解程度,某調(diào)查小組隨機抽取了某市物化生、政史地的![]() 名高中生,請他們列舉鐘南山院士在醫(yī)學上的成就,把能列舉鐘南山成就不少于
名高中生,請他們列舉鐘南山院士在醫(yī)學上的成就,把能列舉鐘南山成就不少于![]() 項的稱為“比較了解”,少于三項的稱為“不太了解”他們的調(diào)查結(jié)果如下:
項的稱為“比較了解”,少于三項的稱為“不太了解”他們的調(diào)查結(jié)果如下:
組合 | 0項 | 1項 | 2項 | 3項 | 4項 | 5項 | 5項以上 |
物化生(人) | 1 | 10 | 17 | 14 | 14 | 10 | 4 |
政史地(人) | 0 | 8 | 10 | 6 | 3 | 2 | 1 |
(1)請將下面的2×2列聯(lián)表補充完整;
組合 | 比較了解 | 不太了解 | 合計 |
物化生 | |||
政史地 | |||
合計 |
(2)判斷是否有99%的把握認為,了解鐘南山與選擇物化生、政史地組合有關(guān)?
參考:![]()
![]() .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com