
【題目】設數列{an}的各項都是正數,且對任意n∈N* , 都有(an﹣1)(an+3)=4Sn , 其中Sn為數列{an}的前n項和.
(1)求證數列{an}是等差數列;
(2)若數列{ ![]() }的前n項和為Tn , 求Tn .
}的前n項和為Tn , 求Tn .
【答案】
(1)解:∵對任意n∈N*,都有(an﹣1)(an+3)=4Sn,即 ![]() .
.
∴當n≥2時,4an=4(Sn﹣Sn﹣1)= ![]() ﹣
﹣ ![]() =
= ![]() ﹣2an﹣1,
﹣2an﹣1,
化為(an+an﹣1)(an﹣an﹣1﹣2)=0,
∵對任意n∈N*,an>0.
∴an+an﹣1>0.
∴an﹣an﹣1=2.
∴數列{an}是等差數列,公差為2
(2)解:由(1),a1=3,d=2,∴an=3+2(n﹣1)=2n+1.
∴ ![]() =4n(n+1),
=4n(n+1),
∴ ![]() =
= ![]() =
= ![]() ,n∈N*;
,n∈N*;
∴Tn= ![]()
【解析】(1)由已知利用“當n≥2時,an=Sn﹣Sn﹣1”即可求得an與an﹣1的關系,進而證明數列{an}是等差數列.(2)利用(1)可得 ![]() =
= ![]() =
= ![]() ,n∈N* , 再利用“裂項求和”即可得出.
,n∈N* , 再利用“裂項求和”即可得出.


科目:高中數學 來源: 題型:
【題目】已知數列{bn}滿足bn=| ![]() |,其中a1=2,an+1=
|,其中a1=2,an+1= ![]() .
.
(1)求b1 , b2 , b3 , 并猜想bn的表達式(不必寫出證明過程);
(2)由(1)寫出數列{bn}的前n項和Sn , 并用數學歸納法證明.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓O1和圓O2的極坐標方程分別為ρ=2, ![]() .
.
(1)把圓O1和圓O2的極坐標方程化為直角坐標方程;
(2)求經過兩圓交點的直線的極坐標方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知奇函數f(x)是定義在(﹣2,2)上的減函數,則不等式f( ![]() )+f(2x﹣1)>0的解集是( )
)+f(2x﹣1)>0的解集是( )
A.(﹣∞, ![]() )
)
B.[﹣ ![]() ,+∞)
,+∞)
C.(﹣6,﹣ ![]() )
)
D.(﹣ ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=Asin(ωx+φ),x∈R(其中 ![]() )的圖象與x軸的交點中,相鄰兩個交點之間的距離為
)的圖象與x軸的交點中,相鄰兩個交點之間的距離為 ![]() ,且圖象上一個最低點為
,且圖象上一個最低點為 ![]() . (Ⅰ)求f(x)的解析式;
. (Ⅰ)求f(x)的解析式;
(Ⅱ)當 ![]() ,求f(x)的值域.
,求f(x)的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點A(0,2),B(4,6), ![]() =t1
=t1 ![]() +t2
+t2 ![]() ,其中t1、t2為實數;
,其中t1、t2為實數;
(1)若點M在第二或第三象限,且t1=2,求t2的取值范圍;
(2)求證:當t1=1時,不論t2為何值,A、B、M三點共線;
(3)若t1=a2 , ![]() ⊥
⊥ ![]() ,且△ABM的面積為12,求a和t2的值.
,且△ABM的面積為12,求a和t2的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知直線l1:kx+y=0和直線l2:kx+y+b=0(b>0),射線OC的一個法向量為 ![]() =(﹣k,1),點O為坐標原點,且k≥0,直線l1和l2之間的距離為2,點A、B分別是直線l1、l2上的動點,P(4,2),PM⊥l1于點M,PN⊥OC于點N;
=(﹣k,1),點O為坐標原點,且k≥0,直線l1和l2之間的距離為2,點A、B分別是直線l1、l2上的動點,P(4,2),PM⊥l1于點M,PN⊥OC于點N; 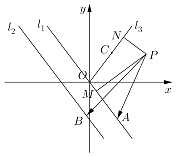
(1)若k=1,求|OM|+|ON|的值;
(2)若| ![]() |=8,求
|=8,求 ![]() 的最大值;
的最大值;
(3)若k=0,AB⊥l2 , 且Q(﹣4,﹣4),試求|PA|+|AB|+|BQ|的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某個部件由三個元件按圖方式連接而成,元件1或元件2正常工作,且元件3正常工作,則部件正常工作(其中元件1,2,3正常工作的概率都為 ![]() ),設三個電子元件的使用壽命(單位:小時)均服從正態分布N(1000,502),且各個元件能否正常工作相互獨立,那么該部件的使用壽命超過1000小時的概率為( )
),設三個電子元件的使用壽命(單位:小時)均服從正態分布N(1000,502),且各個元件能否正常工作相互獨立,那么該部件的使用壽命超過1000小時的概率為( ) 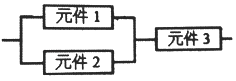
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知公差不為零的等差數列{an}的前4項和為10,且a2 , a3 , a7成等比數列.
(Ⅰ)求通項公式an
(Ⅱ)設bn= ![]() ,求數列{bn}的前n項和Sn .
,求數列{bn}的前n項和Sn .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com