
【題目】如圖,平面![]() 平面
平面![]() ,四邊形
,四邊形![]() 和
和![]() 是全等的等腰梯形,其中
是全等的等腰梯形,其中![]() ,且
,且![]() ,點
,點![]() 為
為![]() 的中點,點
的中點,點![]() 是
是![]() 的中點.
的中點.

(I)請在圖中所給的點中找出兩個點,使得這兩個點所在直線與平面![]() 垂直,并給出證明;
垂直,并給出證明;
(II)求二面角![]() 的余弦值;
的余弦值;
(III)在線段![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]() 平面
平面![]() ?如果存在,求出
?如果存在,求出![]() 的長度,如果不存在,請說明理由.
的長度,如果不存在,請說明理由.
【答案】(I)見解析;(II)![]() ;(III)見解析.
;(III)見解析.
【解析】試題分析: ![]() 法一:向量法,分別以邊
法一:向量法,分別以邊![]() ,
, ![]() ,
, ![]() 所在直線為
所在直線為![]() ,
, ![]() ,
, ![]() 軸,給出相應點坐標,證明
軸,給出相應點坐標,證明![]() ,
, ![]() 法二:先證
法二:先證![]()
![]() 接著證明所以
接著證明所以![]()
![]() 平面
平面![]() 即
即![]() 最后證得結果(2)要求二面角的平面角的余弦值就先求得平面
最后證得結果(2)要求二面角的平面角的余弦值就先求得平面![]() 的法向量,利用公式即可算出結果(3)法一:借助向量假設存在,計算可得
的法向量,利用公式即可算出結果(3)法一:借助向量假設存在,計算可得![]() 矛盾,故不存在;法二:假設存在點
矛盾,故不存在;法二:假設存在點![]() ,證得平面
,證得平面![]() 平面
平面![]() ,即有
,即有![]() 為平行四邊形,所以
為平行四邊形,所以![]() ,矛盾
,矛盾
解析:法一:向量法
(I)![]() ,
, ![]() 點為所求的點.
點為所求的點.
證明如下:
因為四邊形![]() 是等腰梯形,點
是等腰梯形,點![]() 為
為![]() 的中點,點
的中點,點![]() 是
是![]() 的中點,
的中點,
所以![]() .
.
又平面![]()
![]() 平面
平面![]() ,平面
,平面![]()
![]() 平面
平面![]() =
= ![]() ,
,
所以![]()
![]() 平面
平面![]()
同理取![]() 的中點
的中點![]() ,則
,則![]()
![]() 平面
平面![]() .
.
分別以邊![]() ,
, ![]() ,
, ![]() 所在直線為
所在直線為![]() ,
, ![]() ,
, ![]() 軸,建立如圖所示的空間直角坐標系.
軸,建立如圖所示的空間直角坐標系.
由![]() ,得
,得![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
則![]() ,
, ![]() ,
, ![]() .
.
所以![]() ,
, ![]()
又![]() ,
,
所以![]() 平面
平面![]()
(II)由(I)知平面![]() 的一個法向量為
的一個法向量為![]() .
.
設平面![]() 的法向量為
的法向量為![]() ,則
,則
![]() 即
即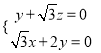
令![]() ,則
,則![]() ,
, ![]()
所以![]()
所以![]()
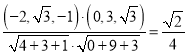
所以二面角![]() 的余弦值為
的余弦值為![]()
(III)假設存在點![]() ,使得
,使得![]()
![]() 平面
平面![]() .
.
設![]()
所以![]()
![]() ,所以
,所以![]()
而計算可得![]()
這與![]() 矛盾
矛盾
所以在線段![]() 上不存在點
上不存在點![]() ,使得
,使得![]()
![]() 平面
平面![]()
法二:(I)證明如下:
因為四邊形![]() 是等腰梯形,點
是等腰梯形,點![]() 為
為![]() 的中點,點
的中點,點![]() 是
是![]() 的中點,
的中點,
所以![]()
![]()
又平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]()
![]() 平面
平面![]()
因為![]()
![]() 平面
平面![]() ,所以
,所以![]() ,
,
又![]() ,且
,且![]() ,
,
所以![]() 為菱形,所以
為菱形,所以![]()
因為![]() ,
,
所以![]() 平面
平面![]() .
.
(III)假設存在點![]() ,使得
,使得![]() 平面
平面![]()
由![]() ,所以
,所以![]() 為平行四邊形,
為平行四邊形,
所以![]()
因為![]() 平面
平面![]()
所以![]() 平面
平面![]()
又![]() ,所以平面
,所以平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,所以
,所以![]() ,
,
所以![]() 為平行四邊形,所以
為平行四邊形,所以![]() ,矛盾
,矛盾
所以不存在點![]() ,使得
,使得![]() 平面
平面![]()


 全能測控期末小狀元系列答案
全能測控期末小狀元系列答案科目:高中數(shù)學 來源: 題型:
【題目】如圖是一段圓錐曲線,曲線與兩個坐標軸的交點分別是![]() .
.

(1)若該曲線為橢圓(中心為原點,對稱軸為坐標軸)的一部分,設直線![]() 過點
過點![]() 且斜率是
且斜率是![]() ,求直線
,求直線![]() 與該段曲線的公共點的坐標.
與該段曲線的公共點的坐標.
(2)若該曲線為拋物線的一部分,求原拋物線的方程.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某工廠利用輻射對食品進行滅菌消毒,現(xiàn)準備在該廠附近建一職工宿舍,并對宿舍進行防輻射處理,建房防輻射材料的選用與宿舍到工廠距離有關.若建造宿舍的所有費用![]() (萬元)和宿舍與工廠的距離
(萬元)和宿舍與工廠的距離![]() 的關系為:
的關系為: ![]() .為了交通方便,工廠與宿舍之間還要修一條簡易便道,已知修路每公里成本為
.為了交通方便,工廠與宿舍之間還要修一條簡易便道,已知修路每公里成本為![]() 萬元,工廠一次性補貼職工交通費
萬元,工廠一次性補貼職工交通費![]() 萬元.設
萬元.設![]() 為建造宿舍、修路費用與給職工的補貼之和.
為建造宿舍、修路費用與給職工的補貼之和.
⑴求![]() 的表達式;
的表達式;
⑵宿舍應建在離工廠多遠處,可使總費用![]() 最小,并求最小值.
最小,并求最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖1,已知知矩形![]() 中,點
中,點![]() 是邊
是邊![]() 上的點,
上的點, ![]() 與
與![]() 相交于點
相交于點![]() ,且
,且![]() ,現(xiàn)將
,現(xiàn)將![]() 沿
沿![]() 折起,如圖2,點
折起,如圖2,點![]() 的位置記為
的位置記為![]() ,此時
,此時![]() .
.


(1)求證: ![]() 面
面![]() ;
;
(2)求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】【選做題】本題包括A、B、C、D四小題,請選定其中兩小題,并在相應的答題區(qū)域內(nèi)作答.若多做,則按作答的前兩小題評分.解答時應寫出文字說明、證明過程或演算步驟.
(1)A.【選修4—1幾何證明選講】
如圖,在△ABC中,∠ABC=90°,BD⊥AC , D為垂足,E是BC的中點,求證:∠EDC=∠ABD.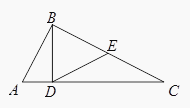
(2)B.【選修4—2:矩陣與變換】
已知矩陣A= ![]() 矩陣B的逆矩陣B﹣1=
矩陣B的逆矩陣B﹣1= 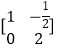 ,求矩陣AB.
,求矩陣AB.
(3)【選修4—4:坐標系與參數(shù)方程】在平面直角坐標系xOy中,已知直線l的參數(shù)方程為 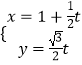 (t為參數(shù)),橢圓C的參數(shù)方程為
(t為參數(shù)),橢圓C的參數(shù)方程為 ![]() (
( ![]() 為參數(shù)).設直線l與橢圓C相交于A , B兩點,求線段AB的長.
為參數(shù)).設直線l與橢圓C相交于A , B兩點,求線段AB的長.
(4)D. 設a>0,|x﹣1|< ![]() ,|y﹣2|<
,|y﹣2|< ![]() ,求證:|2x+y﹣4|<a.
,求證:|2x+y﹣4|<a.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】(本小題滿分12分)△ABC中,角A,B,C所對的邊分別為a,b,c.已知a=3,cos A=![]() ,B=A+
,B=A+![]() .
.
(1)求b的值;
(2)求△ABC的面積.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】海關對同時從![]() 三個不同地區(qū)進口的某種商品進行抽樣檢測,從各地區(qū)進口此種商品的數(shù)量(單位:件)如下表所示,工作人員用分層抽樣的方法從這些商品中共抽取6件進行檢測.
三個不同地區(qū)進口的某種商品進行抽樣檢測,從各地區(qū)進口此種商品的數(shù)量(單位:件)如下表所示,工作人員用分層抽樣的方法從這些商品中共抽取6件進行檢測.
地區(qū) |
|
|
|
數(shù)量 | 50 | 150 | 100 |
(1)求這6件樣品中來自![]() 各地區(qū)商品的數(shù)量;
各地區(qū)商品的數(shù)量;
(2)若在這6件樣品中隨機抽取2件送往甲機構進一步檢測,求這2件商品來自相同地區(qū)的概率.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設f(x)=2 ![]() sin(π﹣x)sinx﹣(sinx﹣cosx)2 .
sin(π﹣x)sinx﹣(sinx﹣cosx)2 .
(1)求f(x)的單調(diào)遞增區(qū)間;
(2)把y=f(x)的圖象上所有點的橫坐標伸長到原來的2倍(縱坐標不變),再把得到的圖象向左平移 ![]() 個單位,得到函數(shù)y=g(x)的圖象,求g(
個單位,得到函數(shù)y=g(x)的圖象,求g( ![]() )的值.
)的值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com