
【題目】點P在圓O:x2+y2=8上運動,PD⊥x軸,D為垂足,點M在線段PD上,滿足 ![]() .
.
(1)求點M的軌跡方程;
(2)過點Q(1, ![]() )作直線l與點M的軌跡相交于A、B兩點,使點Q為弦AB的中點,求直線l的方程.
)作直線l與點M的軌跡相交于A、B兩點,使點Q為弦AB的中點,求直線l的方程.
【答案】
(1)解:∵點M在線段PD上,滿足 ![]() ,
,
∴點M是線段PD的中點,
設M(x,y),則P(x,2y),
∵點P在圓O:x2+y2=8上運動,
則x2+(2y)2=8,
即 ![]() ,
,
故點M的軌跡方程為 ![]() .
.
(2)解:
方法一:當直線l⊥x軸時,由橢圓的對稱性可得弦AB的中點在x軸上,
不可能是點Q,這種情況不滿足題意.
設直線l的方程為 ![]() ,
,
由 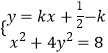 ,
,
可得 ![]() ,
,
由韋達定理可得x1+x2=﹣ ![]() ,
,
由AB的中點為 ![]() ,可得﹣
,可得﹣ ![]() =2,
=2,
解得 ![]() ,
,
即直線l的方程為y﹣ ![]() =﹣
=﹣ ![]() (x﹣1),
(x﹣1),
則直線l的方程為x+2y﹣2=0.
方法二:當直線l⊥x軸時,由橢圓的對稱性可得弦AB的中點在x軸上,
不可能是點Q,這種情況不滿足題意.
設A(x1,y1),B(x2,y2),
A、B兩點在橢圓上,
滿足 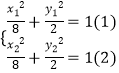 ,
,
由(1)﹣(2)可得 ![]() ,
,
則 ![]() ,
,
由AB的中點為 ![]() ,可得x1+x2=2,y1+y2=1,代入上式
,可得x1+x2=2,y1+y2=1,代入上式 ![]() ,
,
即直線l的方程為y﹣ ![]() =﹣
=﹣ ![]() (x﹣1),
(x﹣1),
∴直線l的方程為x+2y﹣2=0.
【解析】(1)判斷M線段PD的中點,設M(x,y),則P(x,2y),運用代入法,即可得到所求軌跡方程;(2) 方法一、運用直線方程和橢圓方程聯(lián)立,運用韋達定理和中點坐標公式,化簡整理可得斜率k,由點斜式方程可得直線方程;
方法二、設A(x1 , y1),B(x2 , y2),A、B兩點在橢圓上,代入橢圓方程,運用作差法和斜率公式,再由點斜式方程可得直線的方程.


 通城學典默寫能手系列答案
通城學典默寫能手系列答案 金牌教輔培優(yōu)優(yōu)選卷期末沖刺100分系列答案
金牌教輔培優(yōu)優(yōu)選卷期末沖刺100分系列答案科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)f(x)= ![]() +lnx在(1,+∞)上是增函數(shù),且a>0.
+lnx在(1,+∞)上是增函數(shù),且a>0.
(1)求a的取值范圍;
(2)求函數(shù)g(x)=ln(1+x)﹣x在[0,+∞)上的最大值;
(3)設a>1,b>0,求證: ![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】我校為進行“陽光運動一小時”活動,計劃在一塊直角三角形ABC的空地上修建一個占地面積為S(平方米)的矩形AMPN健身場地.如圖,點M在AC上,點N在AB上,且P點在斜邊BC上.已知∠ACB=60°,|AC|=30米,|AM|=x米,x∈[10,20].設矩形AMPN健身場地每平方米的造價為 ![]() 元,再把矩形AMPN以外(陰影部分)鋪上草坪,每平方米的造價為
元,再把矩形AMPN以外(陰影部分)鋪上草坪,每平方米的造價為 ![]() 元(k為正常數(shù)).
元(k為正常數(shù)).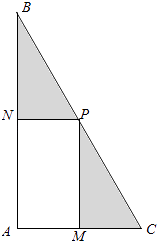
(1)試用x表示S,并求S的取值范圍;
(2)求總造價T關于面積S的函數(shù)T=f(S);
(3)如何選取|AM|,使總造價T最低(不要求求出最低造價).
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】若f(x)=ax2+3a是定義在[a2﹣5,a﹣1]上的偶函數(shù),令函數(shù)g(x)=f(x)+f(1﹣x),則函數(shù)g(x)的定義域為 .
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)f(x)=|x﹣t|+ ![]() (x>0);
(x>0);
(1)判斷函數(shù)y=f(x)在區(qū)間(0,t]上的單調(diào)性,并證明;
(2)若函數(shù)y=f(x)的最小值為與t無關的常數(shù),求實數(shù)t的取值范圍.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com