
【題目】越野汽車輪胎的質(zhì)量是根據(jù)其正常使用的時間來衡量,使用時間越長,表明質(zhì)量越好,且使用時間大于或等于6千小時的為優(yōu)質(zhì)品.現(xiàn)用![]() ,
,![]() 兩種不同型號的汽車輪胎做試驗,各隨機抽取部分產(chǎn)品作為樣本,得到試驗結(jié)果的頻率分布直方圖如圖所示,以上述試驗結(jié)果中各組的頻率作為相應(yīng)的概率.
兩種不同型號的汽車輪胎做試驗,各隨機抽取部分產(chǎn)品作為樣本,得到試驗結(jié)果的頻率分布直方圖如圖所示,以上述試驗結(jié)果中各組的頻率作為相應(yīng)的概率.

(1)現(xiàn)從大量的![]() ,
,![]() 兩種型號的輪胎中各隨機抽取2件產(chǎn)品,求其中至少有3件是優(yōu)質(zhì)品的概率;
兩種型號的輪胎中各隨機抽取2件產(chǎn)品,求其中至少有3件是優(yōu)質(zhì)品的概率;
(2)通過多年統(tǒng)計發(fā)現(xiàn),![]() 型輪胎每件產(chǎn)品的利潤
型輪胎每件產(chǎn)品的利潤![]() (單位:元)與其使用時間
(單位:元)與其使用時間![]() (單位:千小時)的關(guān)系如下表:
(單位:千小時)的關(guān)系如下表:
使用時間 |
|
|
|
每件產(chǎn)品的利潤 |
| 200 | 400 |
若從大量的![]() 型輪胎中隨機抽取兩件,其利潤之和記為
型輪胎中隨機抽取兩件,其利潤之和記為![]() (單位:元),求
(單位:元),求![]() 的分布列及數(shù)學(xué)期望.
的分布列及數(shù)學(xué)期望.
【答案】(1)![]() ;(2)分布列見解析,
;(2)分布列見解析,![]()
【解析】
(1)先根據(jù)直方圖得到抽取一件![]() 和一件
和一件![]() 型輪胎為優(yōu)質(zhì)品的概率,再根據(jù)互斥事件的加法公式和獨立事件的乘法公式可得結(jié)果;
型輪胎為優(yōu)質(zhì)品的概率,再根據(jù)互斥事件的加法公式和獨立事件的乘法公式可得結(jié)果;
(2)據(jù)題意知,![]() 的可能取值為
的可能取值為![]() ,0,200,400,600,800.根據(jù)概率公式求出
,0,200,400,600,800.根據(jù)概率公式求出![]() 的各個取值的概率,再寫出分布列,根據(jù)數(shù)學(xué)期望公式求出數(shù)學(xué)期望即可.
的各個取值的概率,再寫出分布列,根據(jù)數(shù)學(xué)期望公式求出數(shù)學(xué)期望即可.
(1)由直方圖可知,從![]() 型號輪胎中隨機抽取一件產(chǎn)品為優(yōu)質(zhì)品的概率
型號輪胎中隨機抽取一件產(chǎn)品為優(yōu)質(zhì)品的概率![]() ,
,
從![]() 型輪胎中隨機抽取一件產(chǎn)品為優(yōu)質(zhì)品的概率
型輪胎中隨機抽取一件產(chǎn)品為優(yōu)質(zhì)品的概率![]() ,
,
所以從![]() ,
,![]() 兩種型號輪胎中各隨機抽取2件產(chǎn)品,其中至少有3件是優(yōu)質(zhì)品的概率
兩種型號輪胎中各隨機抽取2件產(chǎn)品,其中至少有3件是優(yōu)質(zhì)品的概率
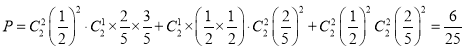 .
.
(2)據(jù)題意知,![]() 的可能取值為
的可能取值為![]() ,0,200,400,600,800.
,0,200,400,600,800.
所以![]() ,
,![]() ,
,
![]() ,
,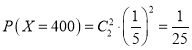 ,
,
![]() ,
,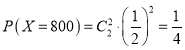 ,
,
那么![]() 的分布列為
的分布列為
|
| 0 | 200 | 400 | 600 | 800 |
|
|
|
|
|
|
|
則數(shù)學(xué)期望![]() .
.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)列{an}滿足a1=![]() ,an+1=3an-1(n∈N*).
,an+1=3an-1(n∈N*).
(1)若數(shù)列{bn}滿足bn=an-![]() ,求證:{bn}是等比數(shù)列;
,求證:{bn}是等比數(shù)列;
(2)求數(shù)列{an}的前n項和Sn.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,在點
,在點![]() 處的切線方程為
處的切線方程為![]() ,求(1)實數(shù)
,求(1)實數(shù)![]() 的值;(2)函數(shù)
的值;(2)函數(shù)![]() 的單調(diào)區(qū)間以及在區(qū)間
的單調(diào)區(qū)間以及在區(qū)間![]() 上的最值.
上的最值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某商場一年購進某種貨物900噸,每次都購進x噸,運費為每次9萬元,一年的總存儲費用為![]() 萬元
萬元
(1)要使一年的總運費與總存儲費用之和最小,則每次購買多少噸?
(2)要使一年的總運費與總存儲費用之和不超過585萬元,則每次購買量在什么范圍?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知四棱錐P﹣ABCD中,四邊形ABCD是菱形,∠BAD=60°,又PD⊥平面ABCD,點E是棱AD的中點,F(xiàn)在棱PC上,且AD=PD=4.

(1)證明:平面BEF⊥平面PAD;
(2)若PA∥平面BEF,求四棱錐F﹣BCDE的體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在三棱拄![]() 中,
中,![]() 側(cè)面
側(cè)面![]() ,已知
,已知![]() ,
,![]() ,
,![]() .
.

(Ⅰ)求證:![]() 平面
平面![]() ;
;
(Ⅱ)試在棱![]() (不包含端點
(不包含端點![]() )上確定一點
)上確定一點![]() 的位置,使得
的位置,使得![]() ;
;
(Ⅲ)在(Ⅱ)的條件下,求![]() 和平面
和平面![]() 所成角正弦值的大小.
所成角正弦值的大小.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() .
.
(1)若展開式中奇數(shù)項的二項式系數(shù)和為128,求展開式中二項式系數(shù)最大的項的系數(shù);
(2)若展開式前三項的二項式系數(shù)和等于37,求展開式中系數(shù)最大的項.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在空間中,給出下列說法:①平行于同一個平面的兩條直線是平行直線;②垂直于同一條直線的兩個平面是平行平面;③若平面![]() 內(nèi)有不共線的三點到平面
內(nèi)有不共線的三點到平面![]() 的距離相等,則
的距離相等,則![]() ;④過平面
;④過平面![]() 的一條斜線,有且只有一個平面與平面
的一條斜線,有且只有一個平面與平面![]() 垂直.其中正確的是( )
垂直.其中正確的是( )
A. ①③B. ②④C. ①④D. ②③
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
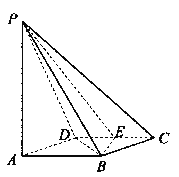
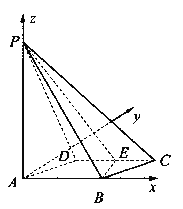
【題目】如圖所示,四棱錐![]() 的底面
的底面![]() 是邊長為1的菱形,
是邊長為1的菱形,![]() ,
,
E是CD的中點,PA![]() 底面ABCD,
底面ABCD,![]() .
.
(I)證明:平面PBE![]() 平面PAB;
平面PAB;
(II)求二面角A—BE—P和的大小.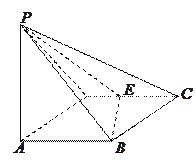
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com