
【題目】如圖所示,在直角坐標(biāo)系![]() 中,點
中,點![]() 到拋物線
到拋物線![]() :
:![]() 的準(zhǔn)線的距離為
的準(zhǔn)線的距離為![]() .點
.點![]() 是
是![]() 上的定點,
上的定點,![]() ,
,![]() 是
是![]() 上的兩動點,且線段
上的兩動點,且線段![]() 的中點
的中點![]() 在直線
在直線![]() 上.
上.
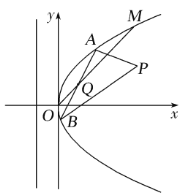
(1)求曲線![]() 的方程及點
的方程及點![]() 的坐標(biāo);
的坐標(biāo);
(2)記![]() ,求弦長
,求弦長![]() (用
(用![]() 表示);并求
表示);并求![]() 的最大值.
的最大值.
【答案】(1)![]() .
.![]() .(2)
.(2)![]() ,
,![]() 的最大值為1.
的最大值為1.
【解析】
(1)根據(jù)拋物線的定義,求出![]() ,即可得出拋物線的方程,便得出點
,即可得出拋物線的方程,便得出點![]() 的坐標(biāo);
的坐標(biāo);
(2)由點![]() ,得出
,得出![]() ,利用點差法求出直線
,利用點差法求出直線![]() 的斜率,得出直線
的斜率,得出直線![]() 的方程為
的方程為![]() ,直線方程與拋物線方程聯(lián)立,寫出韋達定理,利用弦長公式求出弦長
,直線方程與拋物線方程聯(lián)立,寫出韋達定理,利用弦長公式求出弦長![]() ,通過基本不等式求得
,通過基本不等式求得![]() 的最大值.
的最大值.
解:(1)![]() 的準(zhǔn)線為
的準(zhǔn)線為![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴拋物線![]() 的方程為
的方程為![]() .
.
又點![]() 在曲線
在曲線![]() 上,∴
上,∴![]() .
.
故![]() .
.
(2)由(1)知,點![]() ,
,
從而![]() ,即點
,即點![]() ,
,
依題意,直線![]() 的斜率存在,且不為0,
的斜率存在,且不為0,
設(shè)直線![]() 的斜率為
的斜率為![]() ,且
,且![]() ,
,![]() ,
,
由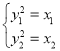 ,得
,得![]() ,
,
故![]() ,
,
所以直線![]() 的方程為
的方程為![]() ,
,
即![]() .
.
由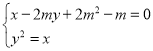 ,消去
,消去![]() ,
,
整理得![]() ,
,
所以![]() ,
,![]() ,
,![]() .
.
從而![]()
![]() .
.
∴![]() ,
,
當(dāng)且僅當(dāng)![]() ,即
,即![]() 時,上式等號成立,
時,上式等號成立,
又![]() 滿足
滿足![]() .
.
∴![]() 的最大值為1.
的最大值為1.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】《中國詩詞大會》亮點頗多,十場比賽每場都有一首特別設(shè)計的開場詩詞,在聲光舞美的配合下,百人團齊聲朗誦,別有韻味.因為前四場播出后反響很好,所以節(jié)目組決定《將進酒》、《山居秋暝》、《望岳》、《送杜少府之任蜀州》和另外確定的兩首詩詞排在后六場,并要求《將進酒》與《望岳》相鄰,且《將進酒》排在《望岳》的前面,《山居秋暝》與《送杜少府之任蜀州》不相鄰,且均不排在最后,則后六場開場詩詞的排法有( )
A. 144種 B. 48種 C. 36種 D. 72種
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在棱長為1的正方體![]() 中,
中,![]() 分別為棱
分別為棱![]() 的中點.
的中點.![]() 為面對角線
為面對角線![]() 上任一點,則下列說法正確的是( )
上任一點,則下列說法正確的是( )

A.平面![]() 內(nèi)存在直線與
內(nèi)存在直線與![]() 平行
平行
B.平面![]() 截正方體
截正方體![]() 所得截面面積為
所得截面面積為![]()
C.直線![]() 和
和![]() 所成角可能為60°
所成角可能為60°
D.直線![]() 和
和![]() 所成角可能為30°
所成角可能為30°
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系中,曲線![]() 是由兩個定點
是由兩個定點![]() 和點
和點![]() 的距離之積等于
的距離之積等于![]() 的所有點組成的,對于曲線
的所有點組成的,對于曲線![]() ,有下列四個結(jié)論:①曲線
,有下列四個結(jié)論:①曲線![]() 是軸對稱圖形;②曲線
是軸對稱圖形;②曲線![]() 上所有的點都在單位圓
上所有的點都在單位圓![]() 內(nèi);③曲線
內(nèi);③曲線![]() 是中心對稱圖形;④曲線
是中心對稱圖形;④曲線![]() 上所有點的縱坐標(biāo)
上所有點的縱坐標(biāo)![]() .其中,所有正確結(jié)論的序號是______.
.其中,所有正確結(jié)論的序號是______.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】
如圖,已知![]() 是以
是以![]() 的直角三角形鐵皮,
的直角三角形鐵皮,![]() 米,
米,![]() 分別是邊
分別是邊![]() 上不與端點重合的動點,且
上不與端點重合的動點,且![]() .現(xiàn)將
.現(xiàn)將![]() 鐵皮沿
鐵皮沿![]() 折起至
折起至![]() 的位置,使得平面
的位置,使得平面![]() 平面
平面![]() ,連接
,連接![]() ,如圖所示.現(xiàn)要制作一個四棱錐
,如圖所示.現(xiàn)要制作一個四棱錐![]() 的封閉容器,其中
的封閉容器,其中![]() 鐵皮和直角梯形
鐵皮和直角梯形![]() 鐵皮分別是這個封閉容器的一個側(cè)面和底面,其他三個側(cè)面用相同材料的鐵皮無縫焊接密封而成(假設(shè)制作過程中不浪費材料,且鐵皮厚度忽略不計).
鐵皮分別是這個封閉容器的一個側(cè)面和底面,其他三個側(cè)面用相同材料的鐵皮無縫焊接密封而成(假設(shè)制作過程中不浪費材料,且鐵皮厚度忽略不計).
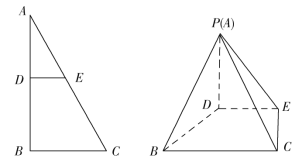
(1)若![]() 為
為![]() 邊的中點,求制作三個新增側(cè)面的鐵皮面積是多少平方米?
邊的中點,求制作三個新增側(cè)面的鐵皮面積是多少平方米?
(2)求這個封閉容器的最大體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】德國著名數(shù)學(xué)家狄利克雷(Dirichlet,1805~1859)在數(shù)學(xué)領(lǐng)域成就顯著.19世紀,狄利克雷定義了一個“奇怪的函數(shù)” 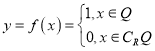 其中R為實數(shù)集,Q為有理數(shù)集.則關(guān)于函數(shù)
其中R為實數(shù)集,Q為有理數(shù)集.則關(guān)于函數(shù)![]() 有如下四個命題,正確的為( )
有如下四個命題,正確的為( )
A.函數(shù)![]() 是偶函數(shù)
是偶函數(shù)
B.![]() ,
,![]() ,
,![]() 恒成立
恒成立
C.任取一個不為零的有理數(shù)T,![]() 對任意的
對任意的![]() 恒成立
恒成立
D.不存在三個點![]() ,
,![]() ,
,![]() ,使得
,使得![]() 為等腰直角三角形
為等腰直角三角形
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)數(shù)列![]() 的前n項和為
的前n項和為![]() ,已知
,已知![]() ,
,![]() ,
,![]() .
.
(1)證明:![]() 為等比數(shù)列,求出
為等比數(shù)列,求出![]() 的通項公式;
的通項公式;
(2)若![]() ,求
,求![]() 的前n項和
的前n項和![]() ,并判斷是否存在正整數(shù)n使得
,并判斷是否存在正整數(shù)n使得![]() 成立?若存在求出所有n值;若不存在說明理由.
成立?若存在求出所有n值;若不存在說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線![]() 過點
過點![]() ,且焦點為F,直線l與拋物線相交于A,B兩點.
,且焦點為F,直線l與拋物線相交于A,B兩點.
⑴求拋物線C的方程,并求其準(zhǔn)線方程;
⑵![]() 為坐標(biāo)原點.若
為坐標(biāo)原點.若![]() ,證明直線l必過一定點,并求出該定點.
,證明直線l必過一定點,并求出該定點.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某地某所高中 2019 年的高考考生人數(shù)是 2016 年高考考生人數(shù)的 1.5 倍,為了更好地對比該校考生的升學(xué)情況,統(tǒng)計了該校 2016 年和 2019年的高考升學(xué)情況,得到柱圖:
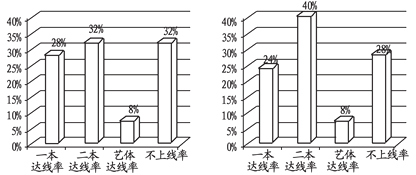
2016年高考數(shù)據(jù)統(tǒng)計 2019年高考數(shù)據(jù)統(tǒng)計
則下列結(jié)論正確的是( )
A.與2016年相比,2019年一本達線人數(shù)有所增加
B.與2016年相比,2019年二本達線人數(shù)增加了0.5倍
C.與2016年相比,2019年藝體達線人數(shù)相同
D.與2016年相比,2019年不上線的人數(shù)有所增加
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com