
【題目】研究下列函數的定義域、值域、奇偶性和單調性,并作出其大致圖像.
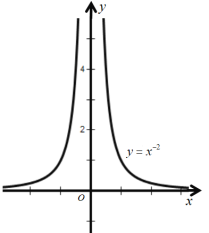
(1)![]() ;
;
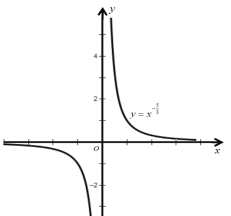
(2)![]() ;
;
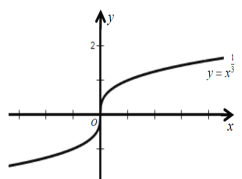
(3)![]() ;
;
(4)![]() .
.
【答案】(1)定義域:![]() ;值域:
;值域:![]() ;偶函數;在
;偶函數;在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減;圖像見解析;(2)定義域:
上單調遞減;圖像見解析;(2)定義域:![]() ;值域:
;值域:![]() ;奇函數:在
;奇函數:在![]() 和
和![]() 上單調遞減;圖像見解析;(3)定義域;R;值域:R;奇函數;在
上單調遞減;圖像見解析;(3)定義域;R;值域:R;奇函數;在![]() 上單調遞增;圖像見解析;(4)定義域:
上單調遞增;圖像見解析;(4)定義域:![]() 值域:
值域:![]() ;非奇非偶函數;在
;非奇非偶函數;在![]() 上單調遞增;圖像見解析
上單調遞增;圖像見解析
【解析】
將冪函數化為根式的形式,分析其定義域和值域,由奇偶性的定義判斷其奇偶性,由指數的正負結合冪函數的性質先判斷出函數在第一象限內的單調性,再根據奇偶性得出單調區間,作出其大致圖像.
(1)![]() ,設
,設![]() ,
,![]() 的定義域為
的定義域為![]() ,
,
因為![]() ,所以值域為:
,所以值域為:![]()
顯然![]() ,
,![]() 為偶函數,
為偶函數,
在![]() 中,
中,![]() ,
,![]() 為偶函數,所以在
為偶函數,所以在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減.
上單調遞減.
(2)![]() ,設
,設![]() ,定義域:
,定義域:![]() ,
,
由![]() ,所以值域:
,所以值域:![]() ,
,
由![]() ,所以
,所以![]() 奇函數,
奇函數,
在![]() 中,
中,![]() ,
,![]() 為奇函數,所以在
為奇函數,所以在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞減.
上單調遞減.
(3)![]() ,設
,設![]() ,所以定義域;R;值域:R;
,所以定義域;R;值域:R;
由![]() ,所以
,所以![]() 奇函數,
奇函數,
在![]() 中,
中,![]() ,在
,在![]() 上單調遞增.
上單調遞增.
(4)![]() ,設
,設![]() ,由
,由![]() 得定義域:
得定義域:![]() 值域:
值域:![]()
因為定義域:![]() ,所以
,所以![]() 非奇非偶函數;
非奇非偶函數;
在![]() 中,
中,![]() ,定義域為
,定義域為![]() ,所以
,所以![]() 在
在![]() 上單調遞增;
上單調遞增;
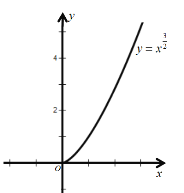


科目:高中數學 來源: 題型:
【題目】如圖,已知點C是圓心為O半徑為1的半圓弧上從點A數起的第一個三等分點,![]() 是直徑,
是直徑,![]() ,直線
,直線![]() 平面
平面![]() .
.
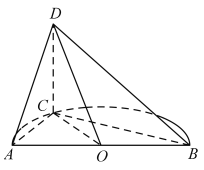
(1)證明:![]() ;
;
(2)若M為![]() 的中點,求證:
的中點,求證:![]() 平面
平面![]() ;
;
(3)求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在空格內填入“充分非必要”或“必要非充分”或“充要”或“既非充分又非必要”.
(1)“![]() ”是“
”是“![]() ”的________條件;
”的________條件;
(2)“![]() ”是“
”是“![]() ”的________條件;
”的________條件;
(3)已知![]() ,
,![]() ,“
,“![]() ”是“
”是“![]() ”的________條件;
”的________條件;
(4)“![]() ”是“
”是“![]() ”的________條件;
”的________條件;
(5)“![]() ”是“AB”的________條件;
”是“AB”的________條件;
(6)“![]() ”是“
”是“![]() ”的________條件;
”的________條件;
(7)“集合AB”是“![]() ”的________條件;
”的________條件;
(8)已知![]() ,“
,“![]() ”是“
”是“![]() ”的________條件.
”的________條件.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】據調查:人類在能源利用與森林砍伐中使CO2濃度增加.據測,2015年,2016年,2017年大氣中的CO2濃度分別比2014年增加了1個單位,3個單位,6個單位.若用一個函數模擬每年CO2濃度增加的單位數y與年份增加數x的關系,模擬函數可選用二次函數![]() (其中
(其中![]() 為常數)或函數
為常數)或函數![]() (其中a,b,c為常數),又知2018年大氣中的CO2濃度比2014年增加了16.5個單位,請問用以上哪個函數作模擬函數較好?
(其中a,b,c為常數),又知2018年大氣中的CO2濃度比2014年增加了16.5個單位,請問用以上哪個函數作模擬函數較好?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,橢圓
中,橢圓![]() :
: ![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,兩焦點與短軸的一個頂點構成等腰直角三角形,且點
,兩焦點與短軸的一個頂點構成等腰直角三角形,且點 在橢圓
在橢圓![]() 上.
上.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)如圖所示,過橢圓的左焦點作直線![]() (斜率存在且不為0)交橢圓
(斜率存在且不為0)交橢圓![]() 于
于![]() 兩點,過右焦點作直線
兩點,過右焦點作直線![]() 交橢圓
交橢圓![]() 于
于![]() 兩點,且
兩點,且![]() ,直線
,直線![]() 交
交![]() 軸于點
軸于點![]() ,動點
,動點![]() (異于
(異于![]() )在橢圓上運動.
)在橢圓上運動.
①證明: ![]() 為常數;
為常數;
②當![]() 時,利用上述結論求
時,利用上述結論求![]() 面積的取值范圍.
面積的取值范圍.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從4名男生和2名女生中任選3人參加演講比賽,設隨機變量ξ表示所選3人中女生的人數.
(1)求所選3人中女生人數ξ≤1的概率;
(2)求ξ的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系![]() 中,以坐標原點為極點,
中,以坐標原點為極點, ![]() 軸的正半軸為極軸建立極坐標系,已知曲線
軸的正半軸為極軸建立極坐標系,已知曲線![]() 的極坐標方程為
的極坐標方程為![]() ,直線
,直線![]() 過點
過點![]() 且傾斜角為
且傾斜角為![]() .
.
(1)求曲線![]() 的直角坐標方程和直線
的直角坐標方程和直線![]() 的參數方程;
的參數方程;
(2)設直線![]() 與曲線
與曲線![]() 交于
交于![]() ,
, ![]() 兩點,求
兩點,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com