
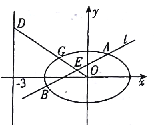
【題目】在平面直角坐標系![]() 中,已知橢圓
中,已知橢圓![]() ,如圖所示,斜率為
,如圖所示,斜率為![]() 且不過原點的直線
且不過原點的直線![]() 交橢圓
交橢圓![]() 于兩點
于兩點![]() ,線段
,線段![]() 的中點為
的中點為![]() ,射線
,射線![]() 交橢圓
交橢圓![]() 于點
于點![]() ,交直線
,交直線![]() 于點
于點![]() .
.
(1)求![]() 的最小值;
的最小值;
(2)若![]() ,求證:直線
,求證:直線![]() 過定點.
過定點.
【答案】(1)![]() .(2)見解析
.(2)見解析
【解析】試題分析:(1)設![]() ,聯立直線和橢圓方程,消去
,聯立直線和橢圓方程,消去![]() ,得到關于的
,得到關于的![]() 一元二次方程,利用韋達定理,求出點
一元二次方程,利用韋達定理,求出點![]() 的坐標和
的坐標和![]() 所在直線方程,求點
所在直線方程,求點![]() 的坐標,利用基本不等式即可求得
的坐標,利用基本不等式即可求得![]() 的最小值;
的最小值;
(2)由(1)知![]() 所在直線方程,和橢圓方程聯立,求得點
所在直線方程,和橢圓方程聯立,求得點![]() 的坐標,并代入
的坐標,并代入![]() ,得到
,得到![]() ,因此得證直線過定點;
,因此得證直線過定點;
試題解析:(1)設直線![]() 的方程為
的方程為![]() ,由題意,
,由題意, ![]() ,
,
由方程組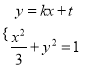 ,得
,得![]() ,
,
由題意![]() ,所以
,所以![]() ,
,
設![]() ,
,
由根與系數的關系得![]() ,所以
,所以![]() ,
,
由于![]() 為線段
為線段![]() 的中點,因此
的中點,因此![]() ,
,
此時![]() ,所以
,所以![]() 所在直線的方程為
所在直線的方程為![]() ,
,
又由題意知![]() ,令
,令![]() ,得
,得![]() ,即
,即![]() ,
,
所以![]() ,當且僅當
,當且僅當![]() 時上式等號成立,
時上式等號成立,
此時由![]() 得
得![]() ,因此當
,因此當![]() 且
且![]() 時,
時, ![]() 取最小值
取最小值![]() .
.
(2)證明:由(1)知![]() 所在直線的方程為
所在直線的方程為![]() ,
,
將其代入橢圓![]() 的方程,并由
的方程,并由![]() ,解得
,解得 ,
,
又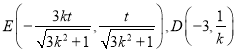 ,
,
由距離公式及![]() 得
得
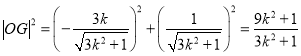 ,
, 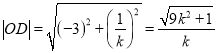 ,
,
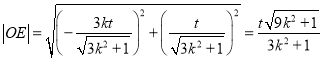 ,
,
由![]() ,得
,得![]() ,
,
因此直線![]() 的方程為
的方程為![]() ,所以直線
,所以直線![]() 恒過定點
恒過定點![]() .
.


 新活力總動員暑系列答案
新活力總動員暑系列答案 龍人圖書快樂假期暑假作業鄭州大學出版社系列答案
龍人圖書快樂假期暑假作業鄭州大學出版社系列答案科目:高中數學 來源: 題型:
【題目】已知O為坐標原點,設動點M(2,t)(t>0).
(1)若過點P(0,4 ![]() )的直線l與圓C:x2+y2﹣8x=0相切,求直線l的方程;
)的直線l與圓C:x2+y2﹣8x=0相切,求直線l的方程;
(2)求以OM為直徑且被直線3x﹣4y﹣5=0截得的弦長為2的圓的方程;
(3)設A(1,0),過點A作OM的垂線與以OM為直徑的圓交于點N,求證:線段ON的長為定值,并求出這個定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐P﹣ABC中,△ABC是等邊三角形,D是AC的中點,PA=PC,二面角P﹣AC﹣B的大小為60°; 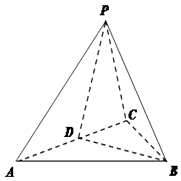
(1)求證:平面PBD⊥平面PAC;
(2)求AB與平面PAC所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】連續拋擲同一顆均勻的骰子,令第i次得到的點數為ai , 若存在正整數k,使a1+a2+…+ak=6,則稱k為你的幸運數字.
(1)求你的幸運數字為3的概率;
(2)若k=1,則你的得分為5分;若k=2,則你的得分為3分;若k=3,則你的得分為1分;若拋擲三次還沒找到你的幸運數字則記0分,求得分X的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著人們對環境關注度的提高,綠色低碳出行越來越受到市民重視. 為此貴陽市建立了公共自行車服務系統,市民憑本人二代身份證到自行車服務中心辦理誠信借車卡借車,初次辦卡時卡內預先贈送20積分,當積分為0時,借車卡將自動鎖定,限制借車,用戶應持卡到公共自行車服務中心以1元購1個積分的形式再次激活該卡,為了鼓勵市民租用公共自行車出行,同時督促市民盡快還車,方便更多的市民使用,公共自行車按每車每次的租用時間進行扣分收費,具體扣分標準如下:
①租用時間不超過1小時,免費;
②租用時間為1小時以上且不超過2小時,扣1分;
③租用時間為2小時以上且不超過3小時,扣2分;
④租用時間超過3小時,按每小時扣2分收費(不足1小時的部分按1小時計算).
甲、乙兩人獨立出行,各租用公共自行車一次,兩人租車時間都不會超過3小時,設甲、乙租用時間不超過1小時的概率分別是0.4和0.5;租用時間為1小時以上且不超過2小時的概率分別是0.4和0.3.
(1)求甲、乙兩人所扣積分相同的概率;
(2)設甲、乙兩人所扣積分之和為隨機變量![]() ,求
,求![]() 的分布列和數學期望
的分布列和數學期望![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com